面向CPU＋GPU 异构计算的SIFT特征匹配并行算法

肖 汉，郭运宏，周清雷

（1.郑州大学 信息工程学院，河南 郑州450001；2.郑州师范学院 信息科学与技术学院，河南 郑州450044；3.郑州铁路职业技术学院 电气工程系，河南 郑州450052）

随着摄影测量和计算机视觉的发展，影像特征匹配越发成为遥感资源分析、三维重建和模式识别等领域研究的基本问题.传统的特征点检测算法中，基于模板匹配的特征点检测算法不易设计出大量模板来匹配纹理细腻的特征点；基于边缘检测的特征点检测算法精度不高；基于亮度变化的特征点检测算法受噪声、光照的影响很大.尺度不变特征变换（scale invariant feature transform，SIFT）算法［1］是一种基于尺度空间理论提取影像局部特征的有效算法，SIFT 特征对尺度缩放、旋转、光照变化均保持不变.但是其算法复杂度高、计算时间长，在实时性要求较高的应用场合中受到了限制.

Sinha等［2］提出了基于OpenGL 的SIFT 特征点提取算法，提速10倍左右.Warn等［3］提出了一种运行在混合机群上的SIFT 算法SOHC.袁修国等［4］提出了利用统一计算设备架构（compute unified device architecture，CUDA），在一种变型的SIFT 算法GLOH 上进行并行化，但是GLOH 算法训练出来的投影矩阵只对某类图像起作用，缺乏广泛的适用性.高玉鹏等［5］实现了CUDA－SIFT 算法提取影像匹配特征点.Mikolajczyk 等［6］提出一种GLOH的改进算法，但其匹配效率没有明显提高.田文等［7］提出一种基于CUDA 的尺度不变特征变换快速算法，测试性能达到了CPU 实现的30～50倍.但是从实验数据中无法看出SIFT 算法的执行时间中是否包括了数据传输时间这一关键因素.

综上所述，采用以CPU 为核心的多核机、并行集群的传统计算资源和传统的OpenGL 图形API开发模式等方式来换取效率，均难以满足在保证影像匹配质量的同时人们对系统性能提升的要求.与此同时，图形处理器（GPU）的可编程能力和并行处理能力越来越强大.为此，本文提出一种对SIFT 特征匹配算法进行多级并行优化的并行算法.实验结果表明，在考虑了CPU－GPU 间数据传输时间的情况下，SIFT 特征匹配GPU 并行算法较CPU 串行算法速度提高了近30倍，大幅缩短数据处理的时间，实时性有了很大的提高.

1 GPU 及CUDA架构

NVIDIA 公司推出的CUDA 模型是一个全新的软硬件基础架构，它以更便捷的方式将GPU 的计算能力开放出来.

1.1 Tesla 2 GPU 并行计算构架

Tesla 2架构中的所有可编程的计算任务都由流处理器阵列（streaming processor array，SPA）执行.SPA 的结构可以被分为两层：第一层是由若干个线程处理器集群（thread processor cluster，TPC）组成的整个阵列，以构成核心计算框架；第二层是组成TPC的若干个流多处理器、一条纹理流水线和一个与渲染输出单元通信的端口.

GPU 执行通用并行计算处理任务时的工作流程：首先GPU 通过PCI－Express总线与主板北桥芯片组通信，从CPU 及内存中读入工作负载到输入装配单元，然后由计算分配单元将输入装配单元取出的计算线程组成的协作线程阵列分发到SPA 中的各个TPC中执行.

1.2 CUDA编程模型

CUDA 采用串－并行混杂的编程模式.任务组织和发送是在CPU 中完成，每当CPU 遇到需要并行计算的任务，则将要做的运算组织成内核kernel.将内存中需要计算的数据从内存由北桥经过高速的PCI－Express总线复制到显存中，再由GPU 执行设备端程序，在计算结束后由主机端程序将结果数据从显存复制到内存.CUDA 可以通过kernel创建出成千上万个线程，然后将这些线程送到GPU 中的上百个核上去运行.

2 SIFT匹配算子描述

2.1 建立多尺度空间

一幅二维影像，在不同尺度下的尺度空间表示可由影像与高斯核空间域卷积得到，如式（1）所示.

式中：G（x，y，σ）代表尺度可变的二维高斯函数；⊗代表卷积运算；I（x，y）代表输入影像；L代表影像的尺度空间.为了有效地在尺度空间检测到稳定的关键点，Lowe提出了利用高斯差分函数（difference of Gaussian，DOG）对原始影像进行卷积，如式（2）［1］所示.

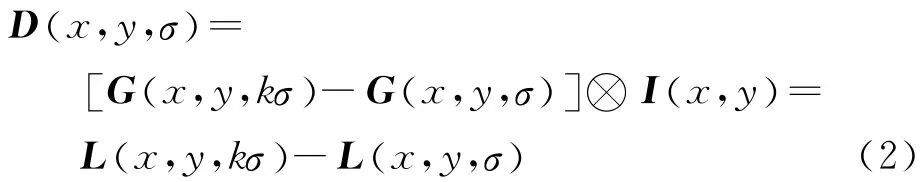
式中：k为不同的高斯核尺度，k的初值为1，尺度以k倍递增.图1为生成高斯差分尺度空间的示意图.

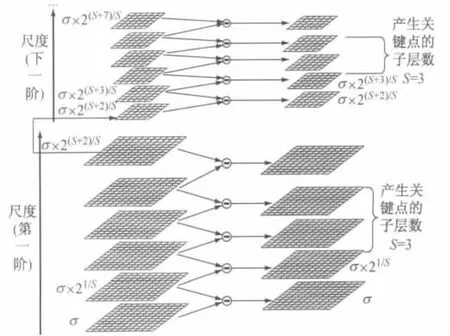
图1 高斯差分尺度空间的生成Fig.1 Generation of scale－space in the difference of Gaussian

2.2 尺度空间关键点检测及精确定位

在高斯差分金字塔影像中间S层中，将影像中的每个点和它同尺度的八邻域点以及上下相邻尺度对应的9×2个邻域点比较是否为极值点，如为极值点则记录其所处的位置和对应的尺度，该点即为候选特征点.检测到的所有极值点就是SIFT 候选特征点的集合［8］.

由于DOG 算子会产生较强的边缘响应，还需要舍弃低对比度的特征点和不稳定的边缘响应点，经过进一步的检验才能精确定位为关键点，以增强匹配的稳定性，提高抗噪声能力［9］.

2.3 关键点方向参数的确定

利用关键点邻域像素的梯度方向分布特征为每个关键点指定方向参数，如式（3）和（4）所示.式中：m（x，y） 和θ（x，y）分别为高斯金字塔影像（x，y） 处梯度的模值和方向，L所用的尺度为每个关键点各自所在的尺度.

2.4 提取特征描述符

SIFT 特征匹配算法关键点由4×4共16 个种子点组成，每个种子点有八个方向的向量信息.将每个种子点的八方向向量信息依次排序，对于每个关键点就能够产生128个数据，形成4×4×8 共1×128维的特征向量即SIFT 特征描述符，记特征描述向量为此时的SIFT 特征描述符已经去除了尺度变化、旋转、变形因素和抗噪声的影响［10］.最后将特征向量长度进行归一化，可以进一步增强对光照变化的鲁棒性［11］.

2.5 SIFT特征匹配

当两幅影像的SIFT 特征描述符生成以后，采用关键点特征描述符的欧氏距离作为两幅影像中关键点的相似性判定度量.

3 SIFT特征匹配并行算法分析与设计

3.1 SIFT特征匹配并行计算模型

在SIFT 特征匹配算法中进行的高斯金字塔影像的构建过程中，每一子层的建立是相对独立的.在尺度空间极值点检测过程中，子层与子层之间并无任何数据通信.特征匹配时在寻找左影像中某个关键点的匹配点的遍历计算中也是相互独立完成，数据之间并无依赖关系.据此，SIFT 特征匹配GPU 并行化处理执行模式如图2所示.

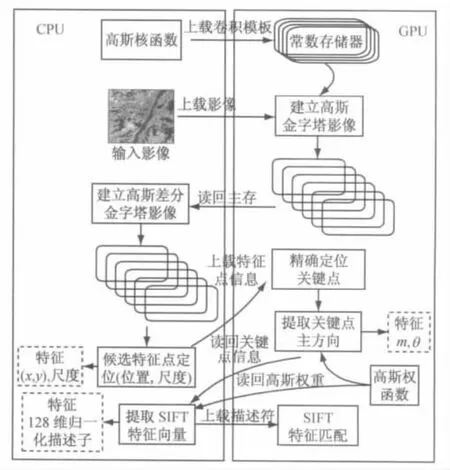
图2 SIFT 特征匹配并行算法执行模式Fig.2 Execution mode of parallel algorithm for SIFT feature matching

SIFT 特征匹配并行计算具体过程为：①首先利用CPU 读取输入影像到主存，将不同尺度的高斯核数据由主存传入到GPU 的常数存储器中.在GPU 中进行分步连续滤波加速高斯尺度空间金字塔的构建，并将高斯金字塔存储在全局存储器内.然后高斯金字塔影像被回读到CPU，相邻尺度的两个高斯影像相减得到DOG 金字塔多尺度空间表示.随后在CPU 中检测高斯差分尺度空间中的局部极值点（最大值或最小值），并记录其所处的位置和对应的尺度.这是因为在GPU 上建立多尺度的DOG 空间并确定局部极值点所花费的时间超过通过一个小的回读把数据传递到CPU 上进行计算的时间.当把候选特征点集合信息上传至GPU 中后，便可在GPU 内对高斯差分金字塔所有候选特征点进行精确定位.计算关键点周围影像强度的主曲率，通过一个2×2的Hessian矩阵计算特征值比率，检测关键点主曲率是否超过设定的阈值，通过去掉多余的点后，确定关键点集合并精确标记关键点的位置、尺度.关键点位置、尺度将在GPU 中恢复.②利用在GPU 中计算的关键点集合信息，启动kernel计算在关键点附近像素的梯度大小和方向.利用已经存储在全局存储器中的高斯权重函数，对关键点邻域窗口内的各像素的梯度大小进行高斯加权并累加建立方向直方图，检测直方图的峰值，确定关键点主方向.③计算128维的SIFT 描述符.以关键点为中心的16×16影像数据块根据关键点的尺度、位置和方向构造SIFT 描述符的过程，在CPU 上实现则可以发挥CPU 逻辑分支、判断能力强的优势，高效地完成任务.④SIFT 特征匹配，确定匹配点位.按照原始点的自然顺序将维度数据读入共享存储器，优化的重点是距离计算.首先必须保证每个维度差值的平方在同一时刻被计算，而不是使用内循环方式.其次必须保证维度数目中间结果的累加方式高效.

基于GPU 的SIFT 特征匹配算法通过并行性分析，将许多计算分割在CPU 和GPU 之间分别计算，发挥了各自的计算优势，充分体现了CPU＋GPU 异构计算的强大能力.

3.2 基于CUDA 的并行化数据结构

3.2.1 卷积并行

（1）卷积层特征映射

多阶高斯金字塔影像特征映射集可描述为一个由两个二维数组构成的数据结构，即

式中：M，N分别为影像大小的行列数；K为高斯卷积窗口大小；i＝0，1，2，…，O－1；j＝0，1，2，…，5.Lij表示O阶六层高斯金字塔影像特征映射集，为一二维数组.

以层为单位，映射到CUDA 上后，构成一个一维的数组集，如式（6）所示.

式中：＿Li表示第i阶高斯金字塔特征映射集，且为一维数组.｛＿Iij［M×N］，＿Gij［K×K］｝为第i阶第j层特征映射集，每层特征映射共享一个kernel，同时接收来自上层特征映射结果.所有＿Li特征映射集组成Lij.

在主机端上将影像数据读入内存并传输到设备内存中，根据问题的规模和处理方式来确定需要的网格的个数.在GPU 中进行高斯金字塔影像的计算，需要为计算配置六个处理内核，用于对要处理的问题进行划分.每一个kernel配置项包括问题的分块数GridDim 以及每个块内线程数BlockDim.对于一幅row × col 的影像，高斯滤波窗口选取为GAUSSIANDIM × GAUSSIANDIM，Grid栅格大小和kernel启动的执行配置如下：

（2）棋盘式卷积

卷积过程是一个顺序运算的过程，主要包括两步，分别是系数的卷积乘计算和积的累加计算.棋盘式并行计算卷积乘原理如图3所示，其中T为线程.

图3 棋盘式卷积乘示意图Fig.3 Schematic diagram of chessboard convolution multiplication

在内核gaussConvolution启动后，待处理的影像数据就存放在全局存储器中，高斯核函数数据存放在常数存储器中.block中各个线程将对应的全局存储器和常数存储器的数据取出完成卷积乘运算后存入共享存储器中.根据单指令多线程执行模型的工作原理可知，活动warp是以时间片分配的：线程调度程序定期从一个warp切换到另一个warp，以最大限度利用多处理器的计算资源.在同一个warp中的32个线程是被绑定在一起执行同一指令的.

当block中所有线程卷积乘计算完毕后，采用并行归约求和算法计算出影像中某个像素点的卷积值.最后将计算结果通过主机端控制从设备端转移到主机端的内存.

3.2.2 线程的任务分配及映射策略

（1）剔除边缘点并行计算中线程的任务分配及映射

在候选特征点检测完成后，形成了一个线性数据结构集合.因此可以分配一个线程去完成是否剔除一个边缘点的判断.通过CUDA 在每个block中开辟512个线程并行判断是否保留该候选特征点.候选特征点位置与线程块中的某一个线程在整个网格中的一维编号之间的地址映射关系为

（2）欧氏距离并行计算中线程的任务分配及映射

关键点的128维描述子可以看成是一个线性数据结构集合，因此可以分配一个线程去完成一对相应维度的差平方计算，其线程地址映射关系为tid＝threadIdx.x.通过CUDA 在每个block 中开辟128个线程并行计算出每一对维度的差平方值，并将结果保存到共享存储器中，每个线程还负责一对差平方值的求和，其地址映射关系为bid＝blockIdx.x.

4 实验结果与分析

4.1 实验运算平台

硬件平台：GPU 为GeForce GTX 285，含有30颗流多处理器，240颗CUDA 核，其核心频率为648 MHz，CUDA 核频率为1 476 MHz，显存位宽为512 bit，显存带宽为159GB·s－1.CPU 为Intel i7Quad Core 2.67GHz，系统内存为4.0GB.

软件平台：操作系统为Microsoft Windows XP，Visual Studio C＋＋ .NET 2005，CUDA Driver 190.38，CUDA Toolkit 2.3.

4.2 实验步骤与数据记录

为了进行多组数据的对比实验，首先对原始影像数据进行预处理，通过裁剪获得影像大小分别为101×128，135×187，284×375，489×561，687×765，784×832，874×962，1 082×1 174，1 200×1 435，1 521×1 689，1 782×1 847，2 045×2 184和2 350×2 570共13组实验数据.

图4a和b是影像大小为687×765的原始影像对，图4c和d为对原始影像对采用11×11滤波窗口进行CPU 串行处理SIFT 特征匹配和GPU 并行处理SIFT 特征匹配.

以经过预处理的13幅不同影像大小的影像对，滤波窗口为21×21进行SIFT 特征匹配对比实验，分别运行SIFT 特征匹配的CPU 系统和GPU 系统，并记录处理时间，见表1.以489×561影像大小的影像对进行不同滤波窗口大小的SIFT 特征匹配对比实验，分别运行SIFT 特征匹配的CPU 系统和GPU 系统，并记录处理时间，见表2.

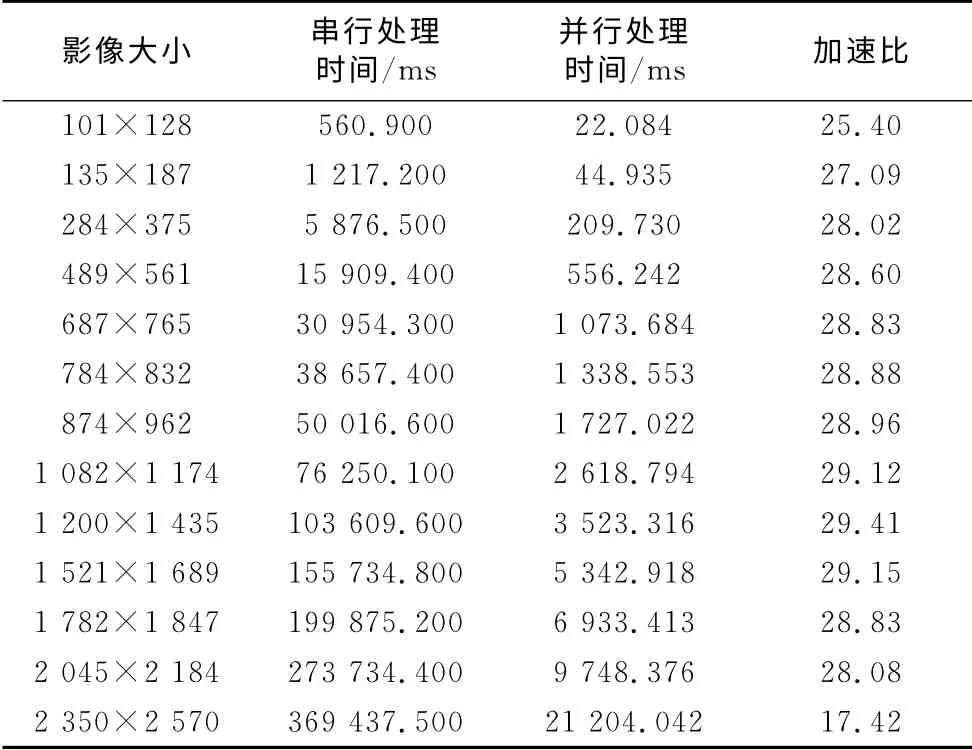
表1 不同影像大小SIFT 特征匹配串并行性能对比Tab.1 Serial and parallel SIFT feature matching algorithm performance comparison of different image sizes

表2 不同滤波窗口SIFT 特征匹配串并行性能对比Tab.2 Serial and parallel SIFT feature matching algorithm performance comparison of different filter windows

4.3 性能分析

左、右影像提取的特征点数分别为52 456，54 265，匹配成功点数8 137；利用定向参数统计匹配点上下视差，中误差5.32μm（0.546个像素）.

实验结果表明：随着影像大小的提高和滤波窗口的增大，GPU 的加速效果十分明显.例如：对影像大小为1 200×1 435 的影像进行SIFT 特征匹配GPU 运算，加速比达到了近30 倍.对滤波窗口为21×21的影像进行SIFT 特征匹配GPU 运算，加速比达到了25倍.

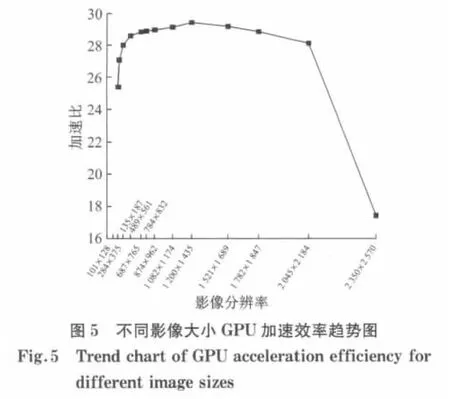
图5和6列出了基于GPU 的SIFT 特征匹配并行算法的加速比对比曲线图.从图5可以看出，当影像大小较小时，随着影像大小的增大，GPU 的加速比有一个小幅上升过程并达到峰值.当影像大小超过1 200×1 435之后，加速比曲线开始出现一个比较平缓的下降过程，但是当影像大小达到2 350×2 570时出现了较陡峭的下降趋势.这主要是由于当影像大小较大时，由于总线带宽的限制，显存－主存间大量的数据通信耗时较多，出现了明显的通信瓶颈现象.

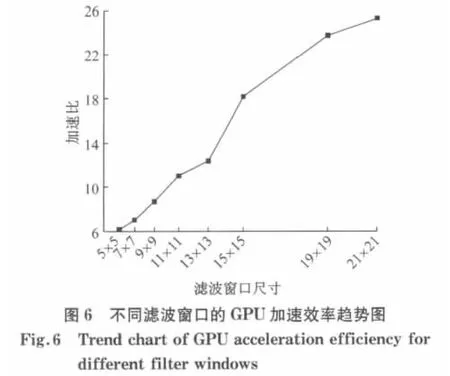
从图6可以看出，随着影像滤波窗口的增大，曲线斜率急剧变大，曲线变得十分陡峭，加速比曲线呈现出一种近线性增长的趋势，并行处理的性能提升效果比较明显，这说明对于采用大滤波窗口时系统可以获得较大的加速效果.随着影像滤波窗口的增大，每个线程块中包含的线程数也随之增大，提高访问全局存储器和共享存储器的效率，这样越容易隐藏存储器延时.

5 结语

针对SIFT 特征匹配算法在处理遥感影像中遇到的算法复杂度高、数据量大、计算时间长，导致影像匹配的速度较慢，应用受到了限制这一问题，本文提出了基于单指令多线程处理模式，在GPU 上实现的SIFT 特征匹配并行算法，并具体给出了SIFT 匹配算法实现的步骤和性能优化的方法.实验结果表明，与CPU 计算相比，采用GPU 加速能够获得最大近30倍的加速比.GPU 大量的并行计算单元和超强的计算能力，为遥感影像处理提供了高效、廉价的处理平台，为海量遥感数据高效处理提供新途径.

［1］ Lowe D G.Distinctive image features from scale－invariant keypoints［J］.International Journa of Computer Vision，2004，60（2）：91.

［2］ Sinha S，Frahm J，Pollefeys M，et al.Feature tracking and matching in video using programmable graphics hardware［EB／OL］. ［2007－3－25］.http：／／citeseerx.ist.psu.edu／viewdoc／download？doi＝10.1.1.81.9737＆rep＝rep1＆type＝pdf.

［3］ Warn S，Apon A，Cothren J.Accelerating SIFT on hybrid clusters［C］／／Proceedings of the ACM SIGSPATIAL 2nd International Workshop on High Performance and Distributed Geographic Information Systems.［S.l.］：ACM SIGSPATIAL，2011：2－9.

［4］ 袁修国，彭国华，王琳.基于GPU 的变型SIFT 算子实时图像配准［J］.计算机科学，2011，38（3）：300.YUAN Xiuguo，PENG Guohua，WANG Lin.GPU－based real time image registration with variant SIFT ［J］.Computer Science，2011，38（3）：300.

［5］ 高玉鹏，何明一.动态背景下基于帧间差分与模板匹配相结合的运动目标检测［J］.电子设计工程，2012，20（5）：142.GAO Yupeng，HE Mingyi.Moving target detection combined two frame differences with template matching methods under dynamic background ［J］.Electronic Design Engineering，2012，20（5）：142.

［6］ Mikolajczyk K，Schmid C.A performance evaluation of local descriptors［J］.IEEE Trans Pattern Analysis and Machine Intelligence，2005，27（10）：1615.

［7］ 田文，徐帆，王宏远，等.基于CUDA 的尺度不变特征变换快速算法［J］.计算机工程，2010，36（8）：219.TIAN Wen，XU Fan，WANG Hongyuan，et al.Fast scale invariant feature transform algorithm based on CUDA ［J］.Computer Engineering，2010，36（8）：219.

［8］ Jonathan Horgan，Francis Flannery，Daniel Toal.Towards real time vision based UUV navigation using GPU technology［C］／／OCEANS 2009－EUROPE.Bremen：［S.l.］，2009：1－6.

［9］ Seth Warn， Wesley Emeneker，Jackson Cothren，et al.Accelerating SIFT on parallel architectures ［C］／／ IEEE International Conference on Cluster Computing and Workshops.［S.l.］：IEEE，2009：1－4.

［10］ YU Qiao，WEI Wang，LIU Jianzhuang，et al.A theory of phase singularities for image representation and its applications to object tracking and image matching［J］.IEEE Transactions on Image Processing，2009，18（10）：2153.

［11］ Marko Heikkilä， MattiPietikäinen， Cordelia Schmid.Description of interest regions with local binary patterns［J］.Pattern Recognition，2009，42（3）：425.