公路岩质边坡应力监测离心模型试验与应用

郭永建，谢永利，牛富生

（1.同济大学 岩土及地下工程教育部重点实验室，上海200092；2.长安大学 公路学院，陕西 西安710064）

随着我国西部山区高速公路建设的不断发展，人为开挖产生的大量岩质边坡的稳定性影响着公路安全运营.一般在设计与施工中均对该类边坡进行锚杆支护，若能够对支护锚杆进行应力监测评价边坡的安全状况，则既经济又能及时预警.

在岩质边坡的失稳过程中，研究人员可以通过现场试验监测的方式获得应力的变化规律，继而提出应力监测的预警值.因此如何获取应力变化规律变得尤为重要，仅仅依靠现场监测很难满足预警研究的要求.鉴于此，本文提出离心模型试验与现场试验相结合的研究手段来实现岩质边坡内部应力变化规律的获取.离心模型试验的机理是通过增加岩体的自重使边坡失稳，更加真实地重现实际边坡在重力作用下的失稳过程.

岩质边坡离心模型试验的研究由来已久.Stewart等［1］利用离心模型试验研究边坡的倾倒破坏，是使用离心模型试验研究边坡失稳的首次尝试.陈祖煜等［2－5］将倾斜台与离心机相结合研究岩质边坡的倾倒破坏，同时首次将锚固系统施加到边坡当中，并利用“人造石”作为岩体替代材料，模拟结构面存在时的岩质边坡破坏模式.邓卫东等［6］采用碎石加泥浆胶结的方式模拟完全碎裂型路堑岩质边坡的破坏形式，并利用离心模型试验得出了碎裂边坡的破坏形式是自上而下的过程.冯振等［7］通过离心模型试验重现了斜倾厚层岩质斜坡视向滑动的“后部块体驱动－前缘关键块体瞬时失稳”模式.在现场试验研究上，何满潮等［8－9］在利用超前滑动力的物理模型试验验证应力监测可行性的基础上，将应力监测和远程监测预报系统相结合，对多处滑坡做出了及时预警.

已有的文献中，国内外学者对于岩质边坡破坏机理进行离心模型试验和现场研究［10－20］，取得了一定的成果.但对于加入锚固系统并进行应力监测的离心模型试验研究还较少.因此，开展应力监测下的岩质边坡破坏过程的土工离心模型试验具有较大的研究和参考意义.本文以广陕高速公路的一段岩质边坡工程为例，采用离心模型试验与现场试验的方法对应力监测存在的问题做进一步研究.

1 工程概况

广陕高速K54＋240～K54＋336位置处的岩质边坡为三级边坡，高30m，每级边坡高均为10m，其中一、二级边坡坡度为1.00∶0.75，三级边坡坡度为1∶1.工程地质概况如图1所示，该边坡为砂岩夹泥岩，受多组结构面与软弱泥岩夹层的影响，实际岩层为单斜结构，岩层产状为339°∠8°.根据地表地质调绘和边坡区基岩露头量测统计，主要发育两组裂隙：∠67°，微张，裂隙面较平直；∠75°，闭合～微张，裂隙面较平直.结合地质勘察资料，认为该边坡潜在的滑动面有三种可能，如图2所示，分别为3 6 7型、2 5 6 7型、1 4 5 6 7型三种.

2 边坡离心模型试验方案

2.1 替代材料的选择

模型试验所采用的设备为TLJ－3 型土工离心机，最大离心加速度为200g，最大容量为60g·t，有效半径为2.0m，模型箱尺寸为70cm×50cm×36 cm（长×宽×高）.在离心模型试验中所选择的模型与原型尺寸相似比为1∶100.

砂岩替代材料采用重晶石粉、石英砂、石膏、水按照不同配比制备，岩石材料的相似主要考虑弹性模量、抗剪强度、重度的相似，砂岩替代材料的选取如表1所示，其中以石膏作为胶结剂.通过材料的对比得出替代材料基本同砂岩的刚度与强度以及重度相似，可以利用替代材料制备的岩体进行试验.其中，弱风化砂岩的重度要稍大于替代材料，但是由于弱风化岩位置不处于滑动面，所以较小的重度差异造成的影响基本可以忽略.

结构面与强风化泥岩位置处为边坡潜在滑动面位置，主要考虑抗剪强度的相似.用拌合好的泥浆模拟近似垂直的结构面和泥岩夹层，抗剪强度为13 kPa，内摩擦角为19°，在强度上基本与实际结构面和泥岩夹层处的强度相似.

测试用全长黏结型锚杆替代材料应与实际锚杆保持弹性模量和锚杆直径的相似，若根据相似比选择锚杆尺寸，锚杆的替代材料类似极细的铁丝，直径数量级约为10－2cm，除无法贴设测试元件以外，更无法模拟锚杆与注浆体的黏结效果.通过试验分析采用加工高刚度、高强度钢片（截面为矩形，弹性模量可达200GPa）进行锚杆的模拟，钢片截面积尺寸为1.5cm×0.5cm，钢片上部贴设应变计监测应力变化.锚杆轴力的计算按照弹性问题进行分析，锚杆的弹性模量和应变测量值与加速度没有换算关系，即锚杆应力也不随加速度改变，但轴力数值是与锚杆截面积相关的量，由于截面积随速度值变化转化为原型时也不断变化，轴力表达式可表述为

式中：F为轴力，n为离心加速度，σ为应力，A为锚杆模型截面积.

2.2 试验方案的选取

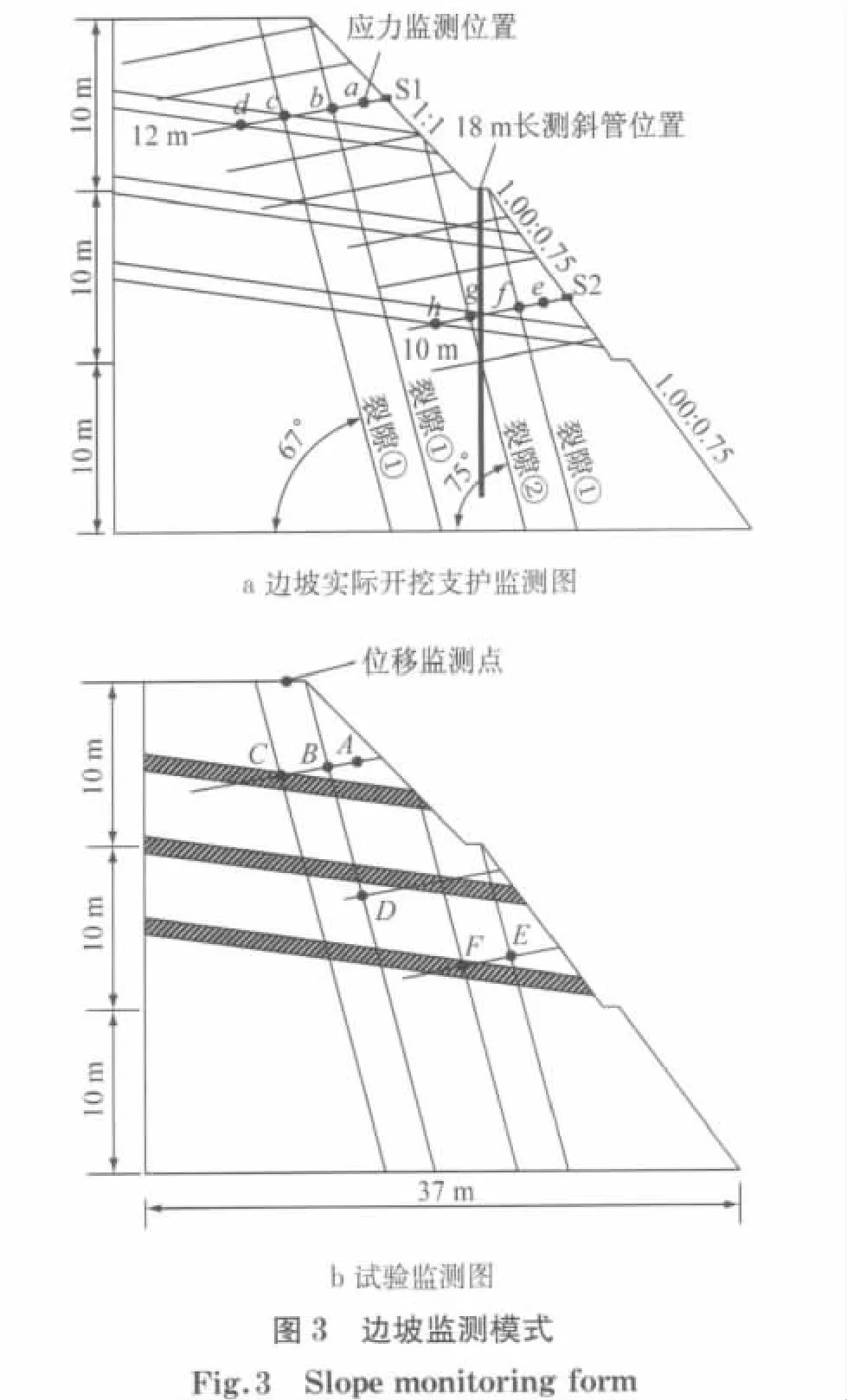
试验设计边坡与实际边坡的开挖支护形式相同，图3a为边坡实际支护与监测方式，二、三级采用锚杆支护，现场边坡开挖支护采用的是由上而下开挖，开挖完成二、三级边坡后再支护的形式，应力监测部位为三、二级边坡的S1与S2两处的锚杆.图3b为试验采用的应力监测位置图，选择A～F点位作为离心模型试验应力监测点位，利用激光位移传感器对坡顶一点的竖向位移进行监测.模型试验的工况为：①无开挖状态的边坡在100g离心加速度下运行30min；②停机开挖三级边坡，在100g离心加速度下运行30min；③停机开挖二级边坡，在100g离心加速度下运行30 min；④停机开挖一级边坡，并支护监测三级、二级边坡，之后不断增加离心加速度直至边坡破坏.

表1 模型试验相似材料设计Tab.1 Similarity material design of model experiment

3 试验结果分析

试验完成时的边坡破坏形式如图4 所示，滑动面为图2所示的1 4 5 6 7型滑动面，属于最深层的破坏形式.图5为边坡开挖支护后直至边坡破坏时的锚杆轴力变化图，其中轴力数据换算为实际边坡尺寸下的锚杆轴力值.边坡破坏时的离心加速度为132g，轴力最大点为C和F两点，均为1 4 5 6 7型滑动面上的点位.图6 为换算为实际边坡尺寸下的坡顶点位的竖向位移随离心加速度变化曲线，与锚杆轴力逐渐变化的曲线相比，位移曲线存在一定的滞后性和突变性，位移值在加速度110g以前基本为零；在加速度增大为122g时位移突然出现明显变化，位移值为12.3cm；在128g时，位移值增大到1.02m；最终在132g时，位移突变为6.51m，边坡破坏.由此可得，采用对边坡顶面位置的点位进行位移监测的方法对边坡失稳进行准确预警，将存在一定难度.

图6 位移－加速度曲线Fig.6 Displacement－acceleration curve

对C和F两点的轴力－加速度变化曲线进行分析，根据曲线形状，采用幂函数进行拟合，拟合结果如图7所示，两者均具有较高的拟合度，可以反映开挖支护后至边坡失稳前的锚杆轴力变化情况.两者均符合幂指数的数学表达形式，在机理上具有相通性，可以用来拟合现场应力监测得出的曲线，并预测其可能的应力增长规律.文献［8］所示的预应力锚索与文献［20］所示的全长黏结锚杆在边坡失稳前的应力变化规律［8，20］，也大致符合幂函数的增长形式，表明离心模型试验的结果是合理的.

图7 轴力－加速度拟合曲线Fig.7 Axial force－acceleration fit curves

根据图7 所示的轴力－加速度拟合曲线和拟合式，提出以离心加速度为105g～115g作为加速度预警范围，此时对应的C点的轴力预警范围为175～208kN，为最大轴力的60%～73%；F点的轴力预警范围为210～255kN，为最大轴力的67%～82%.通过抗拔试验获得现场锚杆的极限抗拔力值为184 kN，由此可以根据预警百分比求解现场的应力监测的轴力预警范围为：C点的轴力预警范围为113～134kN；F点的轴力预警范围为125～151kN.

以下通过现场试验方式对应力监测效果进行评价，并将离心模型试验提出的预警范围进行应用.

4 现场监测结果分析

现场监测分为应力监测与深部位移监测，根据离心模型试验所揭示的边坡潜在滑动面形式，选择监测部位如图3a所示，应力监测部位为三、二级边坡的S1 与S2 两处的锚杆，监测点位表示为a～f点；作为对比，在二级平台位置处埋设长18 m 的测斜管监测边坡内部的水平位移.图8和9为现场试验应力监测结果，二级边坡锚杆轴力最大值出现在g点（对应于离心模型试验的F点），数值为47.1 kN，三级边坡锚杆轴力最大值出现在c点（对应于离心模型试验的C点），数值为13.6kN，出现较大数据变化的点位同离心模型试验基本相同，均未达到离心模型试验得出的预警值.通过监测结果近似可以推断该边坡可能产生的滑动面类型为1 4 5 6 7型，与离心模型试验所揭示的滑动面形式相同.

初始监测时间段内锚杆轴力变化很小，边坡开挖后的应力释放并没有造成太大的下滑力，但在监测时间进行到2010年5月11 日左右时，锚杆轴力突然出现急剧的增加，二级边坡g点的锚杆轴力在20天的时间内由3kN 剧增到47.1kN.对应利用离心模型试验得出的预警范围125～151kN，此时尚未达到预警值，没有预警.但针对该现象的出现相应地增加监测频率，当监测持续到2010年6 月17 日时锚杆轴力开始下降，并在数值上稳定于28.5kN左右.

出现这种锚杆轴力剧增与下降的原因是由于该边坡附近的一处岩质边坡支护不利，受强降雨等因素影响而失稳滑塌，在破坏之前产生的下滑拉力对该边坡造成影响，该影响通过应力监测得到了很好的把握.

边坡深部位移监测结果如图10所示，位移在深度为8m 位置处变化明显，该位置位于1 4 5 6 7型滑动面处，同离心模型试验与应力监测结果相一致.通过对比锚杆轴力变化图8和9与深部位移监测图10，可以得出锚杆轴力在2010年5 月11日左右出现明显变化，而位移则在2010 年6 月10日后才出现明显变化，位移变化明显的时间要稍滞后于应力.长期位移监测结果得出边坡变形趋于稳定，稳定时的变形量约为13.7mm.

综合应力与位移监测的结果，认为该边坡经历旁侧边坡失稳的影响后已基本趋于稳定.

5 结论

（1）结合离心模型试验与现场试验监测的结果确定了岩质边坡的潜在滑动面.

（2）应用离心模型试验揭示了边坡失稳之前的应力变化规律，利用幂函数对得出的监测曲线进行拟合，得出较好的拟合效果.

（3）基于离心模型试验，提出了采用预警百分比的方法来定量地确定应力监测预警值的方法.

（4）现场试验的监测结果表明在复杂的工程现场条件下，产生边坡失稳的因素众多，采用应力监测将能够及时预警各类因素诱发的滑坡.

［1］ STEWART D P，ADHIKARY D P，JEWELL R J.Studies on the Stability of Model Rock Slopes［C］／／Proceedings of the International Conference Centrifuge 94.Singapore：A A Balkema，1994：629－634.

［2］ CHEN Z Y，ZHANG J H，WANG W X，et al.Centrifuge modeling for rock slopes［C］／／Proceedings of the Sixth International Conference on Physical Modelling in Geotechnics.London：Laylor ＆Francis，2006：19－28.

［3］ ZHANG J H，CHEN Z Y.Centrifuge modeling of rock slopes susceptible to block toppling［J］Rock Mechanical and Rock Engineering，2007，40（4）：363.

［4］ 汪小刚，张建红，赵毓芝，等.用离心模型研究岩石边坡的倾倒破坏［J］.岩土工程学报，1996，18（5）：14.WANG Xiaogang，ZHANG Jianhong，ZHAO Yuzhi，et al.Investigations on mechanism of slope toppling failure by centrifuge model testing［J］.Chinese Journal of Geotechnical Engineering，1996，18（5）：14.

［5］ 陈祖煜，汪小刚，杨健，等.岩石边坡稳定分析——原理；方法；程序［M］.北京：中国水利水电出版社，2005.CHEN Zuyu，WANG Xiaogang，YANG Jian，et al.Rock slope stability analysis—theory，method and programs［M］.Beijing：China Water Power Press，2005.

［6］ 邓卫东，吴光勇，唐树名.路堑边坡破坏机理的试验与计算分析［J］.中国公路学报，2001，14（3）：21.DENG Weidong，WU Guangyong，TANG Shuming.Test and calculation on the failure of cutting slope［J］.China Journal of Highway and Transport，2001，14（3）：21.

［7］ 冯振，殷跃平，李滨，等.斜倾厚层岩质滑坡视向滑动的土工离心模型试验［J］.岩石力学与工程学报，2012，31（5）：890.FENG Zhen，YIN Yueping，LI Bin et al.Centrifuge modeling of apparent dip slide from oblique thick bedding rock landslide［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31（5）：890.

［8］ 何满潮.滑坡地质灾害远程监测预报系统及其工程应用［J］.岩石力学与工程学报，2009，28（6）：1081.HE Manchao.Real－time remote monitoring and forecasting system for geological disasters of landsides and its engineering application［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（6）：1081.

［9］ 张鹏，何满潮，陶志刚，等.滑坡灾害远程监控系统的改进及应用效果分析［J］.岩石力学与工程学报，2011，30（10）：2026.ZHANG Peng，HE Manchao，TAO Zhigang，et al.Modification on sliding perturbation remote monitoring system and its application effect analysis［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30（10）：2026.

［10］ Bray J W，Goodman R E.The theory of base friction models［J］.International Journal of Rock Mechanics and Mining Science，1981，18：453.

［11］ Goodman R E. Block theory and its application ［J］.Geotechnique，1995，45（3）：383.

［12］ Goodman R E.Introduction to rock mechanics［M］.New York：John Willey and Sons Inc.，1989.

［13］ 蒋坤，夏才初.基于不同节理模型的岩体边坡稳定性分析［J］.同济大学学报：自然科学版，2009，37（11）：1140.JIANG Kun，XIA Caichu.Stability analysis of jointed rock slopes with different joint constitutive model［J］.Journal of Tongji University：Natural Science，2009，37（11）：1140.

［14］ 娄国充，周德培.软岩高边坡土钉支护的监测分析与优化设计［J］.岩石力学与工程学报，2004，23（16）：2734.LOU Guochong，ZHOU Depei. Monitoring and design optimization of soil－nailing support for high weak rock slope［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（16）：2734.

［15］ 高大水，曾勇.三峡永久船闸高边坡锚索预应力状态监测分析［J］.岩石力学与工程学报，2001，20（5）：653.GAO Dashui，ZENG Yong.Monitoring analysis of prestress state of anchor cable of high slope of the TGP permanent shiplocks［J］. Chinese Journal of Rock Mechanics and Engineering，2001，20（5）：653.

［16］ 张金龙，徐卫亚，金海元，等.大型复杂岩质高边坡安全监测与分析［J］.岩石力学与工程学报，2009，28（9）：1820.ZHANG Jinlong，XU Weiya，JIN Haiyuan.Safety monitoring and stability analysis of large－scale and complicated high rock slope［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（9）：1820.

［17］ 朱焕春.某边坡锚杆应力状态测试与分析［J］.岩土工程学报，2000，22（4）：471.ZHU Huanchun.Measurements and analysis of bolt stresses at a slope［J］.Chinese Journal of Geotechnical Engineering，2000，22（4）：471.

［18］ 何忠明，林杭.节理岩体边坡稳定性的锚杆支护影响分析［J］.公路交通科技，2010，27（11）：8.HE Zhongming，LIN Hang.Influence of bolt reinforcement on stability of rock jointed slope［J］.Journal of Highway and Transportation Research and Developmen，2010，27（11）：8.

［19］ 彭作为，周创兵，龚玉峰，等.向家坝进水口高边坡系统锚杆受力状况研究［J］.岩土力学，2006，27（3）：482.PENG Zuowei，ZHOU Chuangbing，GONG Yufeng，et al.Mechanical analysis of systematic bolts on rock mass in high side slope at intake of Xiangjiaba Hydropower Station［J］.Rock and Soil Mechanics，2006，27（3）：482.

［20］ 徐卫军，李刚.三峡永久船闸直立坡锁口锚杆应力监测分析［J］.长江科学院院报，2001，18（1）：49.XU Weijun，LI Gang.Analysis on monitoring results of locked anchor－bar stress at TGP permanent lock’s vertical slope［J］.Journal of Yangtze River Scientific Research Institute，2001，18（1）：49.