基于数据重复的快速傅里叶算法改进

陈天峰，师剑军，崔 琼

（空军工程大学防空反导学院，陕西 西安 710000）

0 引言

FFT（快速傅里叶算法）作为现代数字处理的一种核心算法，在广阔的领域有着重要的作用，尤其是在雷达测速中。其中分辨率在很大的程度上决定了雷达测速的精度。随着数字系统的发展，人们将傅里叶变换引进到数字系统，形成DFT（数字傅里叶算法）理论。但是，数字傅里叶算法的运算量极大，非常不利于实际应用。20世纪60年代，Cooley和Tukey提出FFT算法解决了这个问题，将N点的DTF的乘法运算量由N2降为log2N［1］。自 从Cooley－Tukey算法提出后，新的算法不断涌现，总体主要有两种趋势：一种是针对N是2的整次幂的算法，如基2算法、基4算法、实因子算法和分裂基算法；一种是针对N不是2的整次幂的算法［2］。在FFT运算中，分辨率与N点采样时间长度成反比，即获得更高的分辨率就大量地增加采样点，进而使得采样时间大幅提高影响了整个FFT的速度。无论哪种算法，现有的FFT改进算法大幅度提高了采样后计算的速度，但是对于解决如何提高分辨率与延长采样时间这对矛盾却没有行之有效的方法。本文针对此矛盾提出了一种基于数据重复使用的快速傅里叶算法。

1 快速傅里叶算法和数据重复

FFT是离散傅里叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后就很容易看出特征了。这就是很多信号采用FFT变换的原因。另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

一个模拟信号，经过ADC采样后就变成了数字信号。接着，就可以进行FFT变换了。

假设采样频率为Fs，信号频率为F，采样点数为N。这样，FFT之后的结果就是一个为N点的复数序列，每一个点对应着一个频率点。其中，第一个点代表的是直流分量（即0Hz），而最后一个点的再下一个点（即第N＋1个点，实际上是不存在的）则表示采样频率Fs。这中间被N－1个点平均分成N等份，每个点的频率依次增加。如此，点n表示的频率为：Fn＝（n－1）＊Fs／N。由上面的公式可以看出，Fn所能分辨到的频率为Fs／N［3］。

举例来说，如果采样频率Fs为1 024Hz，采样点数为1 024点，就FFT可以分辨到1Hz。1 024 Hz的采样率采样1 024点，刚好是1s。也就是说采样1s的信号做FFT，可以分辨到1Hz。如果采样2s并做FFT，则可以分辨到0.5Hz。

上述说明表明，在采样频率固定的情况下，如果FFT要提高频率分辨率，就必须增加采样点数，即增加采样时间。

基于数据重复的快速傅里叶算法就是在基n的Cooley－Tukey算法基础上得来的。

现假设有一离散序列x（n）。对于8点的数字傅里叶变换而言，计算公式为［4］：

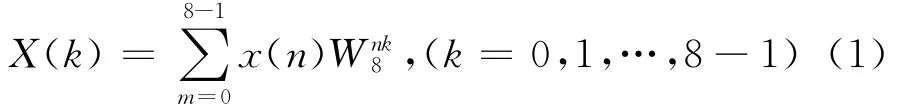
由数字傅里叶的计算公式我们易知乘运算的计算量为82。

而对于同样的序列，8点基2的FFT计算公式为：

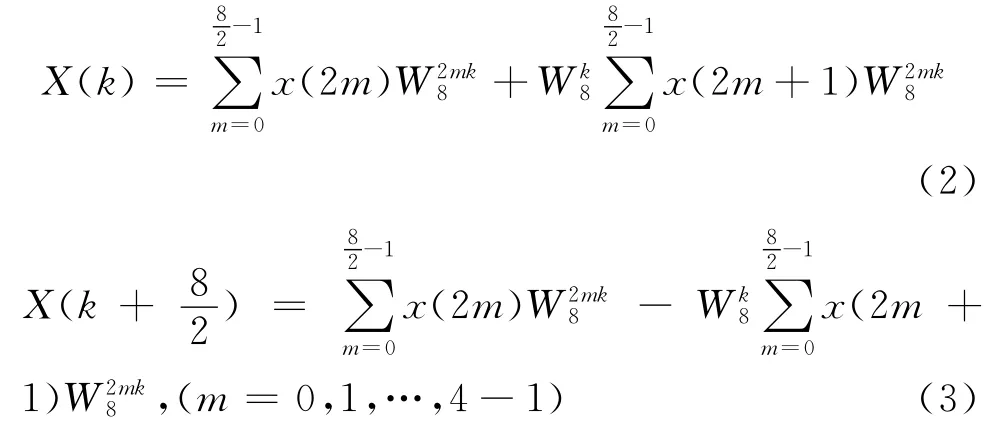
如上述公式所表示，对于8点基2的FFT，后4点的计算的完全利用了前四点的计算数据。如此，FFT就将数字傅里叶的运算量降了下来。

改进算法在一次计算中不但使用了此次采集的数据，而且使用了经过变换的前面若干次采集地数据，从而使得采样点数相应的增加，提高了FFT的分辨率。

为了高效地利用重复数据，先对FFT数据的特点进行分析。下面以8点基2的FFT为例，进行数据内在特点分析。

现假设有一离散序列x（n）。8点基2的FFT计算过程如下：

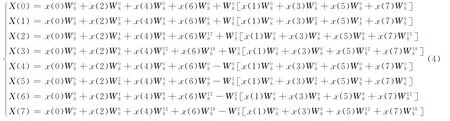
同样地对于更多点数的FFT而言，也会存在类似的关联。数据的重复利用，意味着同一个信号会进行多次FFT变换。现假设分别对第一个点到第八个点，第二个点到第九个点，依次到第八个点到第十五个点，共八组信号进行FFT变换。对于一直参与变换的第八个点，进行系数分析。8点基2的FFT将一次的采样点一分为二，相应的系数相同，故一次FFT的系数只列一半，如下所示：

上述系数，每行是一次变换中的系数，每列是每次变换中同一行的系数。对于这八次变换中，这第八个点构成的数据每次变换的位置变化就是式（4）中每列的变换。反映到上述系数矩阵就是各行系数相同的列之间的替换。

再次带着上述结论去观察上述系数会发现隔行之间存在着简单关系。第一列系数相同，第二列为依次乘以j，第三列依次取反，第四列为依次乘以－j。因为数据存储时实部虚部分别存储，所以其中第二列与第四列的数据可以通过交换实虚部并由条件适当取反实现。

经过上述简单的变换，先前的数据便变得符合这次的变换运算的要求。即数据经过变换后，就可以用于下次的FFT变换了。

2 数据重复快速傅里叶算法思路

对于新的FFT算法，其关键在于将过往数据变换并保存，其与传统的流程对比如图1。

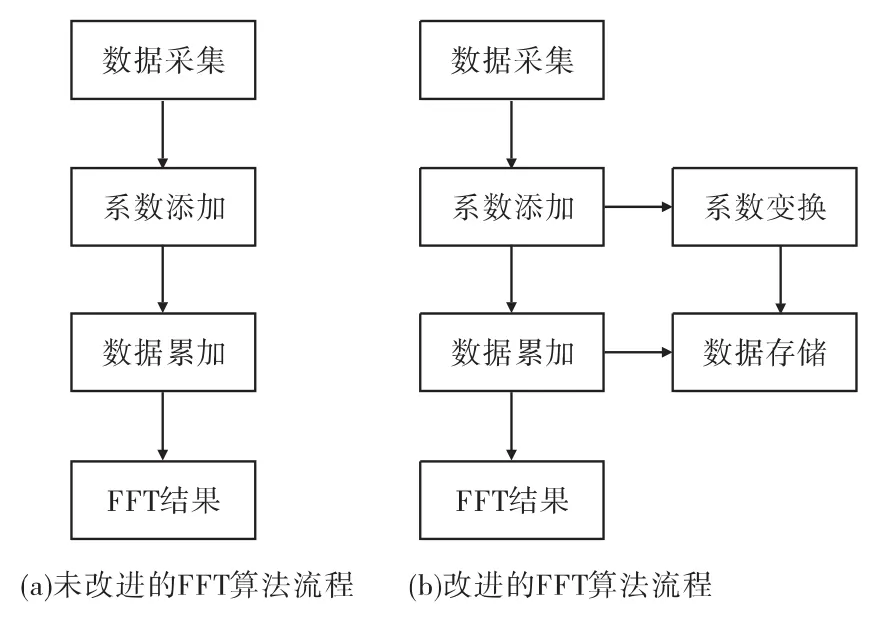
图1 未改进算法与改进算法对比Fig.1 Comparison between the not improved algorithm and the improved algorithm

通过增加了系数变换和数据存储部分，使得对过往数据的利用成为了可能。同时，因为系数变换和数据存储两部分与系数添加是一种并行的关系，因此，这两部分的添加并不会加大运算时间的负担。

在具体的实现过程中，其实现的关键在于存储器结构和计算器的设计。具体而言，使用跳跃分级存储，以及多路相加。同样以8点基2的FFT为例，进行一段时间按之后的FFT的某个数据的存储位置分别为7、5、3、1或者6、4、2、0。图2以其中一路作为例子，图解以便理解。

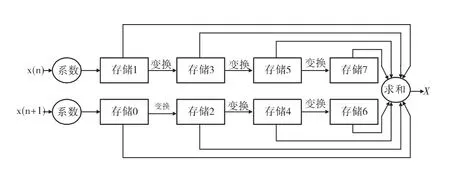
图2 数据重复FFT存储计算图Fig.2 FFT repeated calculation data storage

在实际的设计过程中，采用流水线技术，使得系数变换部分可以在几个周期内顺利完成。从而使得FFT的运算效率进一步加大。

具体而言，系数添加部分到系数变换部分的数据传输应该比这两部分向结果传输数据要有一个固定的延迟，以便于整体数据传输的流畅高效。同时系数添加部分和系数变换部分采用并行运算也是一种有效的方法。

现针对8点基2的FFT，第一次FFT变换使用第一个到第八个数据，第二次使用第三个到第八个数据。第二次FFT变换只采样两个点，对于同样采样率的两点采样FFT，根据分辨率公式，分辨率提高了4倍。

现在将8点基2的FFT向外推广。对于p点基m的FFT。一次FFT变换系数只分析p／m个。对于不同批次的FFT变换，同一个采样点的数据系数变化就是式（4）中单行中各列的变换。由式，可知当k固定时（即计算固定一个频率点时），为了使k的取值不会使得数据重复使用的难度增加，取2 （n1－n2）／p为1／2或者1／2的整数倍。即在数据中，两个数据相距p／4或者p／4整数倍个（在p／m个数据中相距p／4m），就可以使得FFT各行数据系数变换简单易行。

对于实际的一个p点基m的FFT变换来说，数据选择相距p／4时，采样点变作原先的1／4，数据选择相距p／4的a倍时，采样数点变为原先的a／4（a＜m）。对于后续运算，因为只有原先数据的一部分需要重新与系数相乘，故时间上也会大大减少。

3 仿真分析

现在我们以256点的FFT为例，采用Matlab软件中的Simulink模块搭建对0.7·sin（2·π·50·t）＋sin（2·π·120·t）的信号加上一个随机干扰进行3次FFT变换仿真，分别是未进行算法改进的FFT，通过改进采样点数提高2倍的FFT以及采样点数提高4倍的FFT。仿真结果台图3、图4、图5［6］。

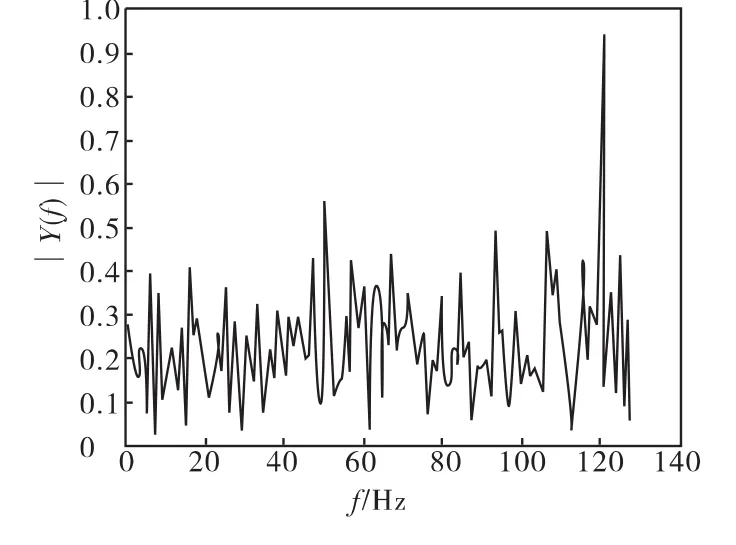
图3 未进行算法改进的FFTFig.3 FFT algorithm without the improvement

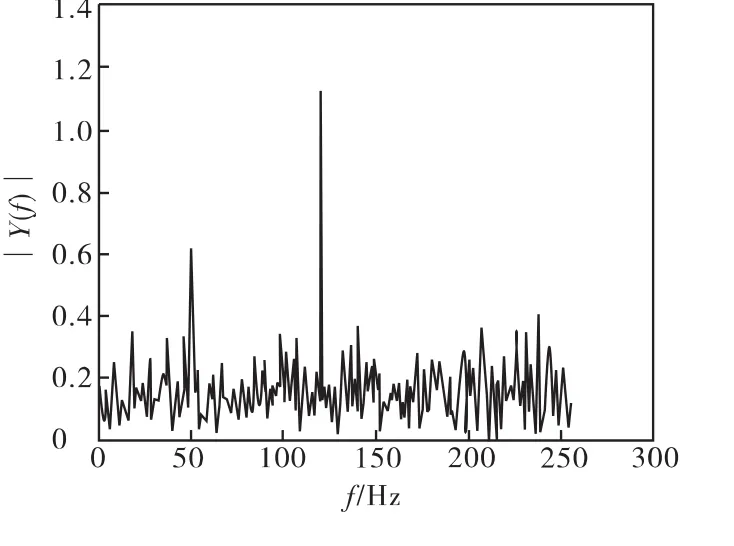
图4 经算法改进的采样点数提高2倍的FFTFig.4 The algorithm to improve the sampling points increased 2times FFT

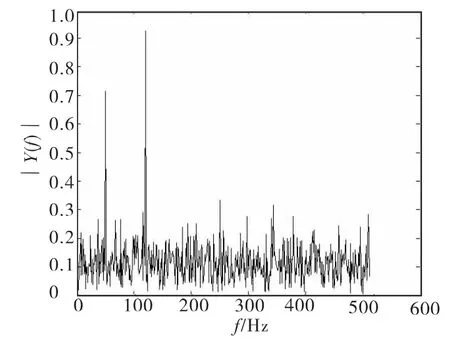
图5 经算法改进的采样点数提高4倍的FFTFig.5 The algorithm to improve the sampling points increased 4times FFT

通过上述3图的对比我们可以发现在未经算法改进的FFT中，频率在120附近的频率点被很好地分离了出来，而频率在50附近的频率点则未能在噪声中分离出来。而经过了算法改进使得采样点提高的FFT中，两个频率点均获得了很好的分离，其中4倍采样点的FFT中两个频率点的幅值均高于噪声幅值3倍以上，很好地分离了频率点，为后续的工作提供了良好的基础。

本文设计的基于数据重复利用的FFT算法，其使用有两种方式：一种是减少采样点，这种方式不仅减少了采样时间，同时在现有的FFT算法上大大地减少了乘法的运算，因而有效地提高了运算速度，因为没有减少参与运算的采样点数，故而分辨率不变；而另一种方式则是采样点不变，但是参与运算的采样点数大大增加，因而大幅度地提高了FFT的分辨率，而每次FFT的后继运算部分，只需重新计算新采样的点数的乘法，故而没有因为参与运算的采样点数的增加而降低速度。

另一方面，算法对于结构的要求并不比传统的FFT高出多少，只是添加一个系数变换部分。这些对于现在的FPGA系统来说是极易实现的。所以说，本算法同样有经济的优点，便于实际应用。

事实上，如果在不考虑系数变换的简易性的基础上，分辨率的提高力度可以进一步加强。但是，这无疑会大大地增加系数变换的结构和控制复杂程度。

4 结论

本文提出基于数据重复利用的FFT算法。该算法通过对过往数据的变换再利用增加了一次FFT运算的点数。仿真表明该算法可以在不明显增加FFT的运算时间的基础上有效地提高FFT的分辨率。该算法不但解决了FFT算法改进中一直无人问津的分辨率与采样时间之间的矛盾，使得FFT的分离效果更为明显，为高速系统的FFT部分的设计提供了一种简单经济可行的选择；而且为FFT算法改进提供了一种新的方向。

［1］Altera.Alter Corporation Cyclone Device Handbook［M］.US：Alter Corpration，2004.

［2］苏涛，吴顺君，廖晓群.高性能数字信号处理器与高速实时信号处理［M］.西安：西安电子科技大学出版社，1999.

［3］胡广书.数字信号处理［M］.北京：清华大学出版社，2003

［4］李春林，伍勇.基于FFT与自相关函数的快速功率谱估计方法［J］.舰船电子工程，2011，31（10）：108－111.LI Chunlin，WU Yong.Fast power spectrum estimation method based on FFT and autocorrelation function［J］.Ship Electronic Engineering，2011，31（10）：108－111.

［5］贾中云，李秀梅，董文.“数字信号处理”中采样定理的教学探索［J］.中国电力教育，2012（29）：79－80.

［6］吴迪，朱金秀，朱昌平.“数字信号处理”课程的教学改革与实践［J］.中国电力教育，2012（32）：78－80.