基于稀疏成份分析的高分辨成像算法

王 良，尚朝轩，何 强，韩壮志

（解放军军械工程学院电子与光学工程系，河北 石家庄 050003）

0 引言

Costas编码信号不存在距离－速度耦合现象，它有理想的图钉形模糊函数，能够同时在距离和速度上实现高分辨。同时Costas编码信号对速度变化非常敏感，速度的变化使相位噪声迅速提高，引起距离像的迅速衰减，最终使距离像淹没在相位噪声里。针对这些特点，为了进行速度补偿，文献［1］将连续波和Costas FH（Frequency Hopping）信号结合设计复合信号，连续波用于测速，这种复合信号增加了系统的复杂性；文献［2］结合波形熵和模拟退火算法设计用于速度的精确搜索算法，然后进行速度补偿，这种算法的时效性有待进一步研究；针对宽带高速目标，文献［3］提出一种Costas编码信号改进的Stretch处理方法，这种方法虽然能够解决宽带高速目标引入的二次相位的影响，但在多目标的环境下，Stretch方法速度补偿不匹配会使整个信号处理的基底噪声增加，基底噪声会将造成大目标对小目标的遮挡效应，尤其是编码个数比较少的时候，遮挡效应更加严重［4］。

稀疏成份分析和实际的物理现象相结合，在信号分析和超分辨重构方面具有很好的应用价值，近几年来受到了广泛的关注，在谱估计、DOA估计、信号重构和成像领域有良好的应用前景［5－6］。对于导弹，子母弹等扩展目标来说，其回波可以认为由有限个散射点回波叠加而成，由于目标尺寸的限制，各个散射点在距离和速度上的差异非常小，但每个散射点对应固定的距离和速度信息，从本质上讲信号是稀疏的。为此，本文通过建立Costas编码信号动目标回波模型，分析目标运动对成像的影响，并根据回波模型构造冗余词典，选择合适的稀疏度量函数，设计约束问题的寻优算法，实现了目标距离－速度二维像的高分辨，丰富的二维像信息更有利于各种导弹目标的探测和识别。

1 Costas跳频信号稀疏性分析

1.1 动目标回波模型

编码个数为N的Costas频率编码脉冲串相参信号的复包络可以表示为

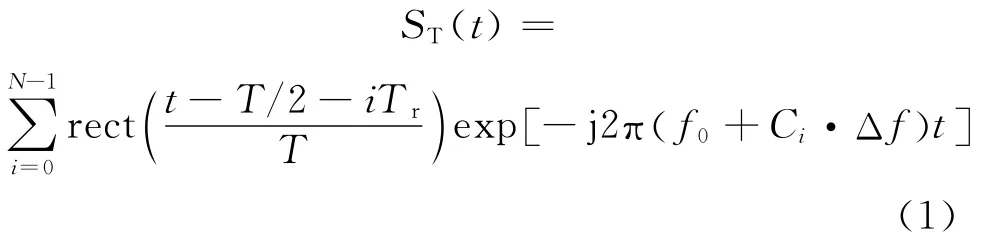
式（1）中f0为发射信号基频，Tr为脉冲重复周期，T为脉冲码元宽度，Δf为步进频率步长，Ci为第i个Costas编码，信号的带宽为B＝NΔf。距离雷达r处的散射点相对雷达的径向运动速度为v，则回波信号的延迟时间为τ（t）＝2（r－vt）／c，回波与本振混频后得到的视频信号为：

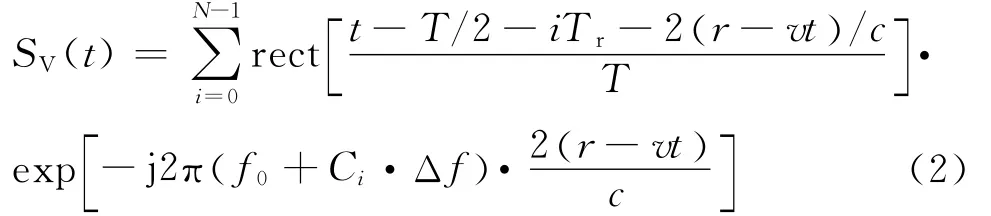
对回波进行码间采样，采样时间为t（i）＝iTr＋T／2＋2r／c，对采样信号重新整序并归一化得到

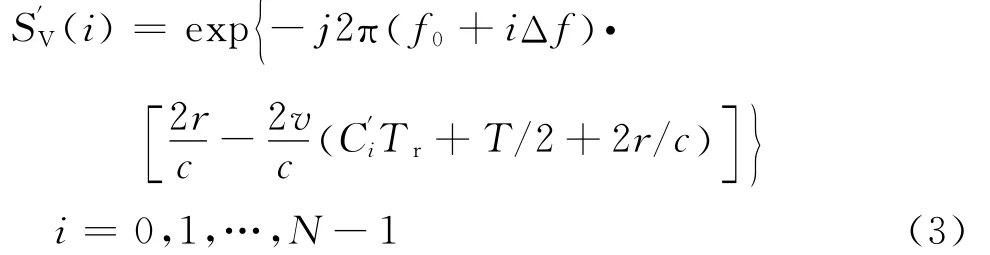
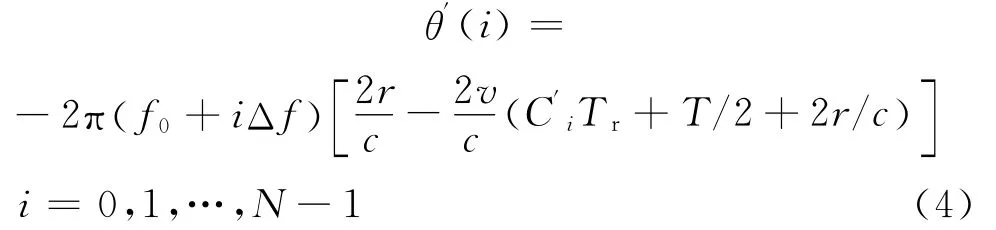
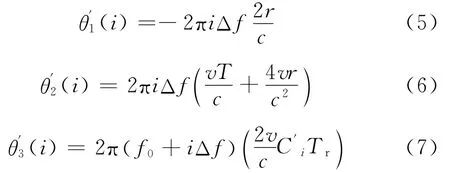
对式（4）作IDFT后即可得到相位（5）～（7）对应的频率信息，频率值的大小对应着距离的大小。的相位积累作IDFT之后峰值的位置对应为目标的距离；由于脉冲宽度T 为 μs级，c为光速，所以≪，可以忽略；顺序重整后的相位积累被打乱，IDFT后表现为噪声的形式，这些噪声和原来的距离像作卷积，会造成散射点距离像的衰减，不会引起距离像位置的变化。

1.2 稀疏成分分析原理

对于给定的观测信号S∈RN，如果存在一个过完备集Φ ＝ ［φ0，φ1，…，φM－1］（称为词典），其中φi∈RN，i＝0，1，…，M－1，rank（Φ）＝N＜M，如果存在系数向量α∈RM满足

则称α为信号S在Φ上的一个表示，如果‖α‖0＜N，则称α为信号S在Φ上的一个稀疏表示。由于Φ的过完备性，式有无穷多组解。如果目标信号源本身具有稀疏特性，那么就可以根据这一先验信息，弥补观测信息不足的缺陷，获得具有超分辨特性的结果。稀疏成份分析就是寻找非零元最少的系数向量α，即求解

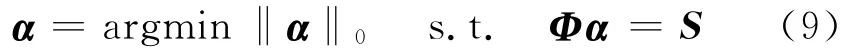
这是一个NP难题，一般采用某种稀疏性度量d（α）来逼近‖α‖0，从而获得稀疏解。

Costas信号有比较理想的图钉形模糊函数，并且随着编码阶数的增加，旁瓣也会降低，模糊函数的图钉形越好，9阶Costas信号模糊函数的数值形式［7］如图1所示。

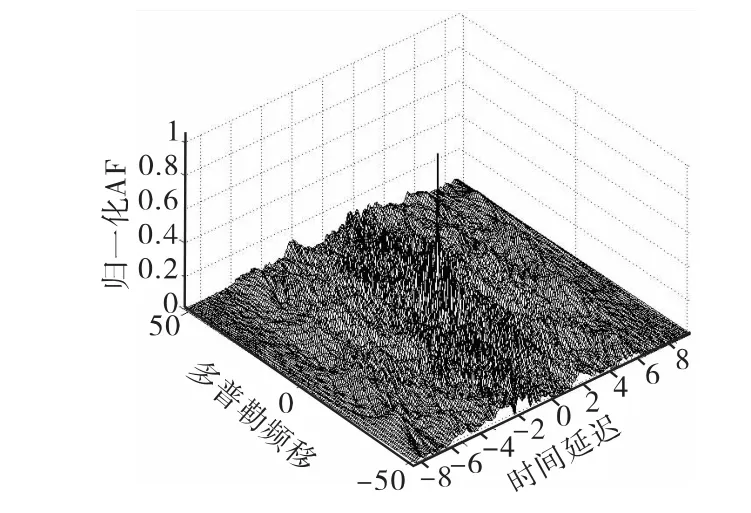
图1 Costas信号的模糊函数（N＝9）Fig.1 Coatas signal ambiguity function（N＝9）

Costas编码信号图钉形的模糊函数表明其距离像对速度非常敏感，并且在距离－速度平面上只有一个峰值，因此，目标在距离－速度平面的二维像是稀疏的；雷达的回波由几个散射中心的回波叠加构成，目标的散射信息在二维距离－速度维上也是稀疏的，这些特性和稀疏成份分析的理论基础是相匹配的，因此，通过构造相应的词典和设计有效的算法，利用稀疏成份分析方法，就可以从低分辨的二维像中重构出高分辨的像。针对稀疏成份分析的过程，主要有吐故纳新和竞争优化两类优化方法可用于寻找具有最稀疏表示特性的解，竞争优化类方法是一个全局优化过程，其中，推广的正则化FOCUSS算法［8］的稀疏度量函数具有更广的选取范围，较易实现。本文针对Costas编码信号对动目标回波模型构造词典，基于推广的正则化FOCUSS算法设计算法，获得目标的高分辨二维像。

2 高分辨二维成像算法

2.1 稀疏词典构造

在毫米波的应用背景下，去掉公式中相对很小以及为常数的相位项，Costas编码信号对于Q个动目标回波可以表示为：

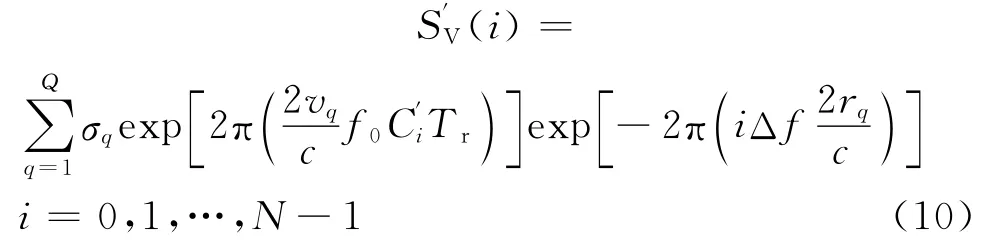
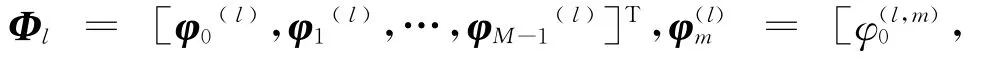
2.2 稀疏重构算法

FOCUSS算法是以最小l2范数解为基础提出的，其基本迭代公式为：

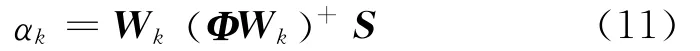
式（11）中，Wk＝diag｛α（k－1）｝；E＋＝EH（EEH）－1表示矩阵E的Moore－Penrose广义逆。根据度量函数的选取规则，并增加信号的稀疏性约束和观测噪声，选取度量函数后公式（9）改写为：

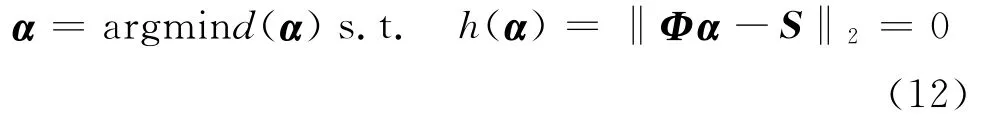
稀疏性度量函数要求该函数在第一象限是凹函数，且关于各分量具有轮换对称性［9］，目前应用较多的主要包括lp≤l－范数和对数函数。稀疏性度量函数d（α）对矢量α的任何一个分量不能有特别的偏好，可以选择可分的度量以保证轮换对称性，即

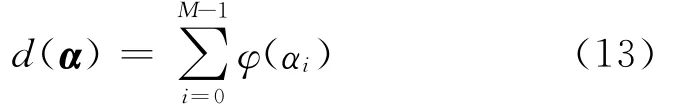
利用惩罚函数法将公式转化为无约束优化模型

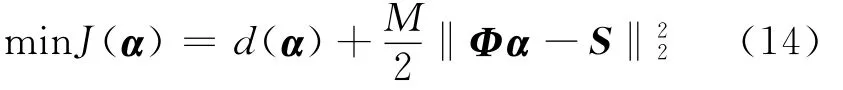
求解式（14）的拟牛顿迭代算法为：

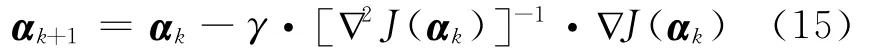
文献［8］结合lp范数，研究了一般性稀疏度量函数应具有的性质，并将正则化FOCUSS算法推广到使用一般性稀疏度量函数的情形，取迭代步长γ＝1，得到推广的正则化FOCUSS算法最优解的迭代公式为

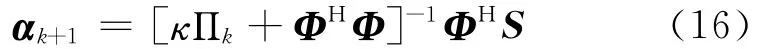
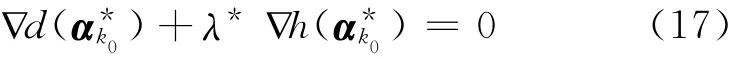
其中λ＊为拉格朗日乘子，不一定为零，因此，一般情况下，目标函数d（α）在约束极小点处的梯度是非零的。采用惩罚函数法经过k0次无约束极小化的最优解满足

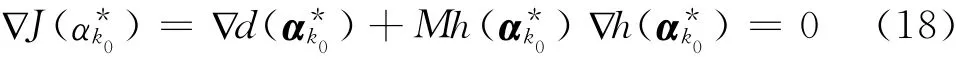
即

这和根据公式（17）得出的结论相矛盾，因此，对于给定的约束问题，惩罚函数法不一定能够通过有限次的无约束的极小化，求得约束问题的极小化问题的最优解，除非d（α）的无约束极小点本身在可行集中。根据乘子法将等式约束的极小化问题转化为：

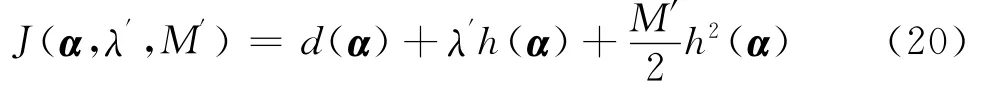
式（20）中λ′为约束极小点处的拉格朗日乘子，这样就可以通过保证无约束的极小化解是约束极小化问题的最优解。假设αk＊为第k次迭代得到的最优解，则

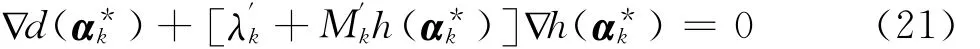
在迭代的过程中，拉格朗日乘子的选取规则为

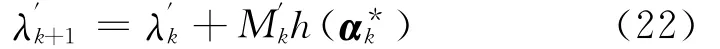
可以使无约束极小化问题快速地收敛到约束问题的最优解。为了优化词典，在构造词典的过程中首先采用脉冲累计的方法进行速度估计，然后在估计的速度周围构造词典，这样可以大大减少词典的维数，减少迭代的次数和计算量。

3 仿真分析

传统雷达系统中采用Stretch信号处理方法，得到不同多普勒频移时目标的距离像［4］。由于受到发射信号时宽和带宽的限制，这种信号处理方法受到距离和速度分辨率的影响，不能分辨在距离和速度上相差小于分辨率的目标。本节结合传统的Stretch方法，对本文的高分辨成像方法进行对比分析。

设置系统参数为：f0＝35GHz，N＝256，B＝300MHz，T＝0.2μs，Tr＝10μs，根据信号的带宽和时宽知道，这种仿真参数下，系统的距离分辨率为Δr＝0.5m，速度分辨率为Δv＝1.67m／s。设置两个点散射体，散射中心距离分别为r1＝289.8m，r2＝290.1m，对应的径向速度分别为v1＝9.7m／s，v2＝10m／s，两个散射体的散射系数为rcs1＝1，rcs2＝0.6。采用Stretch方法进行信号处理，得到的目标距离－速度二维像如图2所示。图2中的二维像只有一个峰值，两个散射体不管是在距离维还是速度维都不能够分辨出来。

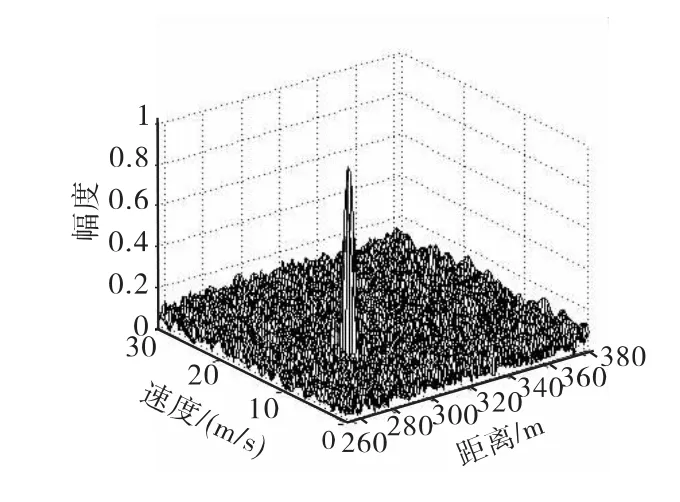
图2 通过Stretch方法得到的二维像Fig.2 2－Dimage through Stretch method

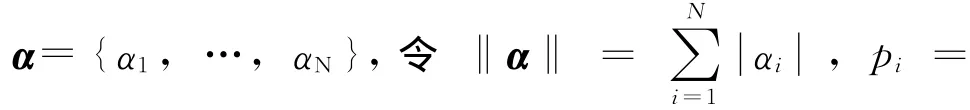
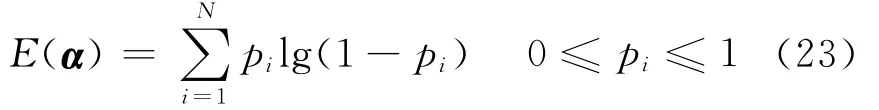
对于一个波形，若其能量沿参数轴分布越均匀，则波形熵越大；反之越小。根据第二节仿真设置雷达发射信号参数，同时在距离为R＝200m的位置设置一个散射点，对散射点赋予不同的速度，计算不同速度时散射点距离像的波形熵，得到波形熵与速度的关系曲线如图3所示。其中纵轴为波形熵，用E表示；横轴为速度，用v表示。仿真表明，一维距离像的波形熵在速度轴上具有全局最小值，且位于散射点的径向速度为零的位置。波形能量沿距离轴发散越严重，对应的波形的稀疏性越差，波形熵的最小值与距离像的最稀疏值相对应，因此，可以用作度量函数进行优化求解。

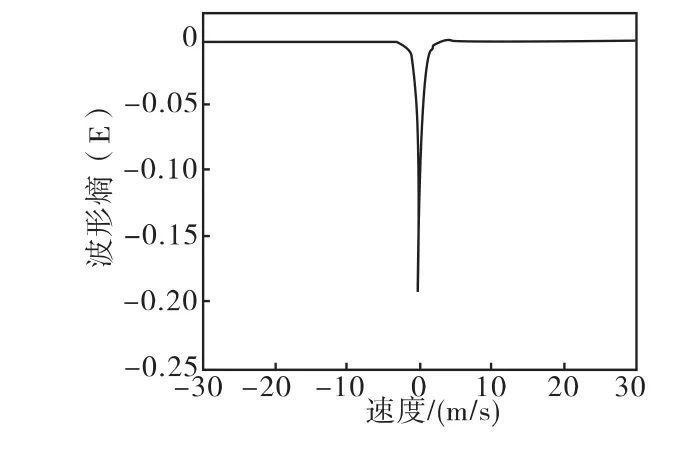
图3 Costas编码信号的波形熵Fig.3 Costas coding signal waveform entropy

设置相同的仿真参数，采用稀疏成份分析进行高分辨成像处理，根据目标距离像的具体位置，在相应的分辨单元构造词典，根据乘子法将等式约束寻优问题转化为无约束寻优问题，设置正则化参数M′＝1，拉格朗日乘子λ′＝0进行仿真，最后得到的仿真结果如图4所示。从图中可以看出，目标的二维像中峰值位置很好地反映了目标的距离和速度信息，稀疏成份分析将理论上不能分开的两个目标很好地区分开了，得到了更高的距离和速度分辨率。和图2相比，通过稀疏成份分析，不仅在散射点的距离和速度维得到了更高分辨率的像，而且散射强度也得到了更准确地估计。

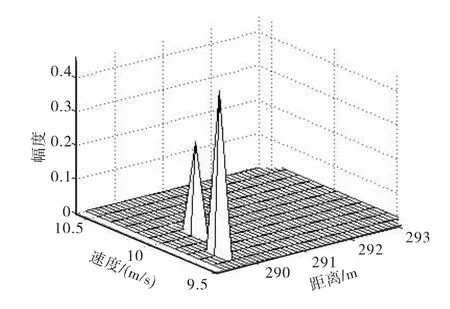
图4 通过稀疏成份分析得到的二维像Fig.4 2－Dimage through sparse compnent analysis

设置更多的散射点，散射点的距离参数为rn＝［228.8，229.1，227.8，228.1，229.8，230.1］m，各散射点对应的速度为vn＝［9.7，10.3，10，9.6，9.5，10.2］m／s，对应的散射系数为rcsn＝［0.5，1，0.7，0.9，0.4，0.8］，这些散射点之间的最大距离超过了距离分辨率，根据上文分析，重新构造词典，进行稀疏成份分析，得到距离－速度二维像如图5所示。图中各个峰值的位置对应目标距离、速度和散射强度的大小，进一步验证了算法的正确性。

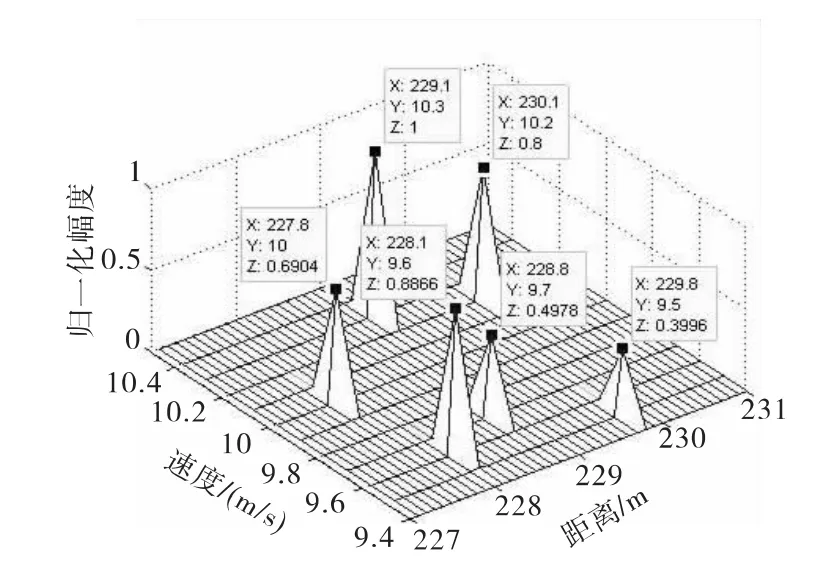
图5 六个散射点通过稀疏成份分析的二维像Fig.5 2－Dimages of 6scattering points through sparse component entropy

4 结论

本文提出一种高分辨的二维成像方法，该方法采用波形熵作为度量函数，构造冗余词典，将乘子法用于推广的正则化FOCUSS算法，求解约束极小化问题的最优解，实现回波信号的稀疏成份分析。仿真表明，相对传统的Stretch方法，这种算法突破了时宽和带宽对距离和速度分辨的约束，实现了二维像在距离－速度上的二维高分辨，同时，避免了大目标对小目标的遮挡效应，实现了散射点距离、速度和散射强度等信息的精确探测。这种算法在提高二维分辨率的同时，也增加了算法的复杂度，更高效的词典构造方法和更快速的实现算法仍需进一步研究。

［1］Mehta S K，Titlebaum E L.A new method for measurement of the target and channel scattering functions using Costas arrays and other frequency hop signals［C］／／A－coustics，Speech，and Signal Processing，1991：1337－1340.

［2］刘静，李兴国，吴文.Costas跳频雷达运动补偿中的模拟退火算法［J］.南京理工大学学报（自然科学版），2004，28（4）：380－384.LIU Jing，LI Xingguo，WU Wen.Simulated annealing algorithm for motion compensation of Costas frequencyhopped radar［J］.Journal of Nanjing University of Science and Technology，2004，28（4）：380－384.

［3］魏玺章，刘振，邓斌，等.Costas编码跳频宽带雷达信号测速技术研究［J］.电子学报，2010，38（10）：2426－2429.WEI Xizhang，LIU Zhen，DENG Bin，et al.Research on velocity measurement of wideband Costas－coded steppedfrequency radar signal［J］.Acta Electronica Sinica，2010，38（10）：2426－2429.

［4］Levanon N.Stepped－frequency pulse－train radar signal［J］.IEE Proceedings－Radar，Sonar and Navigation，2002，149（6）：297－309.

［5］杜小勇，胡卫东，郁文贤.高分辨雷达一维距离像稀疏表示技术［J］.系统工程与电子技术，2005，27（6）：968－970.DU Xiaoyong，HU Weidong，YU Wenxian.Sparse representation technique for high range resolution profiles［J］.Systems Engineering and Electronics，2005，27（6）：968－970.

［6］赵瑞珍，王飞，罗阿理，等.基于稀疏表示的谱线自动提取方法［J］.光谱学与光谱分析，2009，29（7）：2010－2013.ZHAO Ruizhen，WANG Fei，LUO Ali，et al.A method for auto－extraction of spectral lines based on sparse representation［J］.Spectroscopy and Spectral Analysis，2009，29（7）：2010－2013.

［7］Nadav Levanon，Eli Mozesona.Radar Signals［M］.New Jersey：John Wiley ＆Sons，Inc.，2004.

［8］杜小勇，胡卫东，郁文贤.推广的正则化FOCUSS算法及收敛性分析［J］.系统工程与电子技术，2005，27（5）：922－925.DU Xiaoyong，HU Weidong，YU Wenxian.Generalized regularized FOCUSS algorithm and its convergence analysis［J］.Systems Engineering and Electronics，2005，27（5）：922－925.

［9］DU Xiaoyong，HU Weidong，YU Wenxian.A criterion for the construction of a regularization function in sparse component analysis［J］.Circuits，Systems，and Signal Processing，2005，24（4）：315－325.

［10］粟塔山.最优化计算机原理与算法程序设计［M］.长沙：国防科技大学出版社，2001.