改变重复周期的科斯塔斯编码频率捷变引信

崔鹏飞，戴黎红，刘芒龙，张玉波

（1.机电动态控制重点实验室，陕西 西安 710065；2.西安机电信息技术研究所，陕西 西安 710065）

0 引言

频率捷变技术指雷达发射和本地振荡频率高速同步跳变的一种工作方式，是扩展信号频率、增大系统频带的一种有效方法，可以显著提高抗干扰性能；在无线电引信中采用频率捷变技术设计的宽带引信，称为频率捷变引信。

常规捷变频引信中主要应用的是伪随机码，伪随机码的不足之处在于旁瓣较高，容易出现测速和测距的模糊。而Costas编码是公认的捷变频探测体制最优编码方案，其高主瓣、低旁瓣的优点可以有效的改善传统伪随机编码旁瓣高、测距模糊的缺点。但是原始Costas编码其能量又过于集中于主瓣，不易采用简单的信号处理方法测定距离，处理方式复杂。针对其缺点本文提出了采用改变重复周期Costas编码方案。

1 Costas编码

1.1 Costas编码

Costas阵列是由J.P.Costas在1966年提出来的，理论和事实证明，在雷达和声纳系统中采用Costas阵列编码可以准确地确定目标的距离和背离的速度。将Costas阵列运用到频率捷变引信中，即可结合常规捷变频引信的优点，使捷变频引信具有更好的测距性能。

1.2 Costas编码脉冲序列的模糊函数

设跳频雷达脉冲重复周期为T，子脉冲宽度为Tp，频率编码个数为N，脉冲组数为M，频率进步单位步长为Δf，c为光速。令B＝｛b0＋1，b1＋1，…，bN－1＋1｝为Costas编码序列，bi＋1∈ ｛1，2，…，N｝且当i≠k时，bi≠bk，其中i，k＝0，1，…，N－1，biΔf为第i个子脉冲的频载增量，则脉冲编码信号时s（t）的复包络形式可表示为

若bi＝1，则为常规顺序步进频率的脉冲编码信号。

根据模糊函数的定义式：

式中：τ是时延；ε为多普勒频移；s＊（t）是s（t）的共轭函数。将（1）式代入（2）式并经过处理得：

若已知Costas编码序列，将τ和ε离散化，利用卷积的方法可以画出Costas编码脉冲序列和常规顺序步进脉冲序列的模糊函数图。下面取5位Costas阵列为｛1 5 3 2 4｝，分别画出4个周期的Costas编码脉冲序列的三维模糊函数图如图1所示。

2 改变重复周期Costas编码的频率捷变引信

从编码脉冲序列信号的三维模糊图可以看出，Costas编码的脉冲序列信号的模糊图具有理想的图钉形状，能量集中于主瓣，不易采用简单的信号处理方法测定距离。应通过编码方式的改进，使所关心的距离上出现具有一定能量的波瓣。

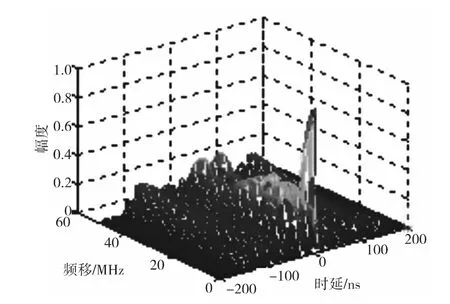
图1 Costas编码模糊图Fig.1 Costas encoding fuzzy graph

2.1 Costas编码的改进

本文通过改变Costas编码的重复周期使所关心的距离上可以出现具有一定能量的波瓣。设改进型Costas编码跳频探测器脉冲重复周期为1.5T，子脉冲宽度为1.5，其中T和Tp分别是标准Costas编码的脉冲重复周期和子脉冲宽度。设频率编码个数为N，脉冲组数为M，频率步进单位步长为Δf，并有Tp＝1／Δf，c为光速。令B＝｛b0＋1，b1＋1，…，bN－1＋1｝为标准 Costas编码序列，bi＋1∈ ｛1，2，…，N｝，且当i≠k时，bi≠bk，其中i，k＝0，1，…，N－1，biΔf为第i个子脉冲的频载增量，则脉冲编码信号s（t）的复包络形式可表示为

将（4）式代入（2）式并经过整理得：

式（5）即为改变重复周期的Costas编码模糊函数定义式。

2.2 改变重复周期Costas编码的频率捷变引信探测器结构图

在结合了Costas编码应用在雷达上的结构简图和捷变频引信的特点给出了改变重复周期Costas编码的频率捷变引信探测器结构图，如图2所示。

图2 改变重复周期的Costas编码的频率捷变引信探测器结构图Fig.2 The structure diagram of Costas coding frequency agile fuse with changing repeating period

图2在原伪随机码频率捷变引信结构的基础上，用Costas调制电压发生器代替了伪随机码调制电压发生器。这种结构对比传统Costas编码信号处理，使用简单的混频——滤波结构，避免了传统结构中的正交检波等复杂运算方法；对比传统伪随机编码信号处理，利用Costas编码旁瓣低的优点，改善了测距模糊。此方法更加适合引信信号处理的特点。

3 仿真验证

3.1 传统伪随机码的仿真

使用MATLAB仿真平台，仿真参数为：跳频间隔10MHz，跳频周期1μs，跳频顺序（32541）。传统伪随机码时延轴模糊图仿真结果如图3所示。

图3 传统伪随机码时延轴模糊图Fig.3 Traditional pseudo－random code delay axis fuzzy graph

由图3可知，伪随机编码跳频体制存在严重的测距模糊，峰值点随距离周期性出现。

3.2 改变重复周期Costas编码的仿真

使用MATLAB仿真平台，由改进型Costas编码的模糊函数定义式（公式（5））可得出改进型Costas编码跳频引信时延模糊图，如图4所示。

图4 改进型Costas编码跳频引信时延模糊图Fig.4 Improved Costas code hopping fuze time－delay fuzzy graph

图4表示改进型Costas编码模糊函数在时延轴上的剖面图。由图可看出目标速度为零时，在100ns（15m）处有对应峰值。

图5 改进型脉间Costas编码跳频引信时延模糊图（局部）Fig.5 Improved Costas code hopping fuze time－delay fuzzy graph（part）

图5是图4的局部放大图，由此图可清楚地看出100ns（15m）处由远及近的首个峰值。

图6是改进型Costas编码跳频序列的模糊图，对应的跳频序列为B＝｛1 5 3 2 4｝，跳频间隔 Δf＝10MHz，跳频周期T＝750ns，子脉冲宽度Tp＝150ns。由图6可知，在目标速度所引起的多普勒频移ξ＝5MHz的情况下，在100ns（15m）处具有明显的峰值。

图7为改进型Costas编码的回波仿真波形图。仿真采用simulink平台，在射频—中频—低频频段进行。仿真参数：调制参数如图5，载波频率f0＝1GHz，弹目相对速度v＝300m／s。仿真结果如图7所示。

由图7可看出在15m处出现由远及近的第一个目标峰值。

图6 改进型Costas编码模糊图Fig.6 Improved Costas coding fuzzy graph

图7 改进型Costas编码的回波仿真波形图Fig.7 Echo simulation waveform of improved Costas coding

4 结论

本文提出了改变重复周期Costas编码的频率捷变引信。该引信在原伪随机码频率捷变引信结构的基础上，用Costas调制电压发生器代替了伪随机码调制电压发生器，并对原始Costas编码进行了改变重复周期的改进。仿真对比表明通过对Costas编码改变重复周期，使得其模糊图在给定距离上出现峰尖，并尽量压缩其他距离处旁瓣能量，改善了传统伪随机码旁瓣较高，容易出现测速和测距的模糊的缺点。而且改变重复周期Costas编码在测距上有着良好的效果，且处理方式简单，为捷变频引信的研制提供了一种可行的调制方法。

但同时可以看出Costas编码序列在目标距离处峰值偏低，而且存在较高的旁瓣能量，可在改变跳频点个数，以及它们的Costas编码序列上进一步研究，以改善目标点处峰值的相对大小。

［1］赵惠昌.无线电引信设计原理与方法［M］.北京：国防工业出版社，2012.

［2］罗贤全，尚朝轩，何强.基于Costas编码跳频雷达信号分析及成像研究［J］.电光与控制，2007（6）：176－179.LUO Xianquan，SHANG Chaoxuan，HE Qiang.Signal analysis and ISAR imaging of frequency hopped radar based on Costas coded array［J］.Electronics Optics ＆Control，2007（6）：176－179.

［3］中航雷达与电子设备研究院.雷达系统［M］.北京：国防工业出版社，2008.

［4］邢孟道.雷达信号处理基础［M］.北京：电子工业出版社，2010.

［5］樊昌信.通信原理［M］.北京：国防工业出版社，2006.

［6］张会宁，任光亮，张辉.频率伪随机捷变引信研究［J］.探测与控制学报，2003，25（2）：12－15.ZHANG Huining，REN Guangliang，ZHANG Hui.Thestudy on pseudo－noise frequency agile fuze［J］.Journal of Detection ＆ Control，2003，25（2）：12－15.