基于统计协方差矩阵的多信道频谱检测算法

仇 帅，陈西宏，刘晓鹏，张 群

（1.空军工程大学防空反导学院，陕西 西安 710051；2.空军工程大学信息与导航学院，陕西 西安 710077）

0 引言

认知跳频系统是将认知无线电中的理论和技术应用到跳频通信中去，通过认知无线电模块对频谱环境进行分析判断，检测“频谱空穴”，发现并及时避开干扰集中的频段，利用检测到的可用频点进行通信，有效地提高了跳频通信对抗干扰的能力［1－4］。频谱检测是CR最核心的关键技术，也是认知跳频系统得以实现的前提和基础。目前比较经典的频谱检测方法主要有匹配滤波法、循环平稳特征检测法、能量检测法等［5－6］。匹配滤波器检测是相关检测的最优检测算法，但需要先验信息及精确同步；循环平稳特征检测在低信噪比情况下具有较好的检测性能，但存在计算量比较大，检测时间长的缺点；能量检测法是一种比较易于实现的检测方法，但容易受到噪声影响，不适用于低信噪比条件的检测。这些方法各有特定的适用条件和缺点。

针对上述经典检测方法的缺陷，近些年来，出现了一些盲检测方法，如基于协方差矩阵的频谱检测和基于特征值的频谱检测，并迅速成为研究热点。文献［7－8］给出了基于统计协方差及特征值分解的检测方法，利用信号与噪声的协方差矩阵的差异性，将信号从噪声背景中区分开来。文献［9］中的检测算法将采样协方差矩阵最大特征值与最小特征值的比值作为统计判决量，并利用最小特征值概率分布求得判决门限。文献［10］研究了新型的基于特征值的感知算法，充分利用随机矩阵的渐近谱分布特性和特征值的收敛性来设置判决门限，提高检测性能。曹开田等对多认知用户采样协方差矩阵的最小特征值进行了研究，获得了比采样协方差矩阵的最大特征值概率分布更合理、更精确的最小特征值概率密度函数，并利用该函数求得更精确的判决门限［11］。这些盲检测算法虽然性能优异，但是只针对单一信道进行检测，即便是对多个信道进行检测时，以往检测算法也只是把多个信道逐个进行检测且门限值相同，而跳频通信系统在通信过程中使用多个频率，存在很多个频率信道，因而上述传统检测算法应用到跳频系统中时存在一定的局限性。

为了克服上述算法的局限性，本文提出了一种基于统计协方差矩阵（statistical covariance matrix，SCM）的多信道频谱检测算法，对于克服认知跳频系统中的部分频带干扰问题有一定参考价值。

1 检测模型及统计协方差矩阵

1.1 认知跳频系统

认知跳频通信系统就是在常规跳频系统中加入CR单元，总体设计框图如图1所示。CR单元主要作用：在跳频发射端检测信道质量，确定被干扰的频点，给出可以使用的跳频频率集，并把信道检测分析结果发送给接收端以保持系统通信的同步。

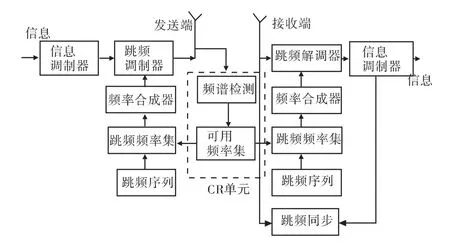
图1 认知跳频系统总体设计方案Fig.1 The overall design scheme of cognitive frequency hopping system

1.2 系统模型及统计协方差矩阵

假设认知跳频系统中的可用信道数为K，每一个信道的采样次数为N，则第i个信道的检测结果可以表述成一个二元假设检验问题：

式中：H0表示信道检测的接收信号中只有背景噪声；H1则表示除了背景噪声还存在干扰信号。其中，xi（n）表示第i个信道在第n时刻采样信号；si（n）表示第i个信道内干扰信号的采样值；ηi（n）表示均值为0、方差为σ2的高斯白噪声。

认知跳频系统对K个信道采样得到的信号构成一个向量：x＝［x1x2…xK］T，其中，xi（i＝1，2，…，K）表示对第i个信道采样N 次得到的信号向量；同理可得s＝［s1s2…sK］T，η＝［η1η2…ηK］T。

假设干扰信号s与背景噪声η互不相关，则在H1成立时，K个信道检测结果的采样协方差矩阵Rx（N）为：

实际检测过程中，统计协方差矩阵R只能由采样协方差矩阵Rx（N）估计得到：

2 基于SCM的多信道频谱检测算法

2.1 干扰信号

本文中的多信道频谱检测主要目的在于发现认知跳频系统信道中干扰严重的频点，利用干扰较小的频率集进行通信。而在众多干扰中部分频带干扰对跳频通信系统的危害最为严重。部分频带干扰的数学建模为［12］：将部分频带干扰模拟为加性高斯噪声，若系统有Q（Q＜K）个信道被干扰，则干扰因子ρ＝Q／K；若干扰功率为J，认知跳频系统总带宽为Wss，则总带宽内的平均干扰单边功率谱密度为PJ＝J／Wss；部分频带干扰的方差为σ12＝PJ／2ρ。

2.2 算法原理

这里将部分频带干扰作为干扰信号s。由式（1）可知，当信道中不存在干扰信号时，si（n）＝0；当第i个信道中存在干扰信号时，si（n）≠0。因此，检测干扰信号只要找到向量s中的非零元素即可。考虑到干扰信号与背景噪声都是实信号，于是，接收信号的统计协方差矩阵为：

其中Rs′为信道检测出的干扰信号的统计协方差矩阵。因为干扰信号为部分频带干扰，所以Rs′为对角矩阵。且Rs′的第i个对角元素为：

又由I为单位矩阵，可以得出R也是对角矩阵，且R的第i个对角元素为：

由式（4）、式（5）可知，区间［1，Q］对应的对角元素数值较大，对应着存在干扰信号的信道；反之，剩余较小的对角元素对应着不受干扰的信道。因此，只要求出统计协方差矩阵R，通过比较其对角元素βi大小，就可以推算出干扰信道。

根据算法的原理分析可知，要检测出信道中存在干扰信号，还必须设定一个判决门限λ：高于此门限值的对角元素，对应着存在干扰信号的信道；反之，信道不存在干扰信号。λ的具体设定方法将在后面的算法流程中给出。

2.3 算法流程

1）信号采样及其协方差计算。对认知跳频信道的检测信号进行采样，并根据公式（2）计算其采样协方差矩阵Rx（N）。

2）求统计协方差矩阵：根据式（3）求出统计协方差矩阵R。

3）判决门限λ的设定。本文采用了两种方法：平均值法和相邻比值法。门限设定的具体步骤如下：

①平均值法：根据上一步求出的量的统计协方差矩阵R，计算其对角元素βi的 均值即为判决门限：

②相邻比值法：将统计协方差矩阵R的对角元素βi从大到小的顺序排列得到βi′。假设χi＝βi′／βi＋1，i＝1，2，…，（K－1），则干扰信道个数Q 的取值应该满足条件χQ＝max（χ1，χ2，…，χK－1）。由χQ＝βQ′／βQ′＋1可知，χQ对应的对角元素βQ′就是判决门限。

4）由协方差矩阵的对角元素βi判决是否存在干扰。

①当用平均值法设定判决门限时，对统计协方差矩阵R的对角元素βi，若βi≥βavg，则表明βi对应的信道中存在干扰信号；反之，说明该信道不存在干扰信号。

②当用相邻比值法设定判决门限时，对统计协方差矩阵R的对角元素βi，若βi≥βQ′，则表明βi对应的信道中存在干扰信号；反之，说明该信道不存在干扰信号。

3 性能仿真分析

本节利用Matlab对认知跳频系统的多信道频谱检测算法进行仿真来分析其检测性能。为了凸显效果，将能量检测法也用于多个频率信道的频谱检测，将二者进行比较。假设认知跳频系统中的可用信道数为K，系统有Q（Q＜K）个信道被干扰，单个信道干扰检测概率为Pd，检测虚警率Pf，则全部信道存在干扰的检测概率为；

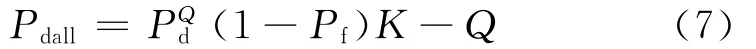
为了分析方便，这里假设认知跳频系统中存在10个频率信道，干扰信号为部分频带干扰，干扰因子ρ＝0.5，即有一半的信道存在干扰信号。由式（7）可知，当Pf较大时，即使干噪比很高，Pdall也无法趋近于1，这就说明即使干扰功率很大，也无法保证准确检测出所有信道中的干扰信号。因此，Pf的值应该设置的尽量小，以保证所有信道的整体检测准确性。在本次仿真中，Pf＝0.001。

图2给出了认知跳频多信道检测法与能量检测法的检测性能曲线，其中，认知跳频多信道检测法据决门限的设定分别采用两种方法：相邻比值法和平均值法。可以看出，整体上，认知跳频多信道检测算法性能优于能量检测法。而在采样点数一样的情况下，采用平均值法的多信道检测算法性能又略优于采用平均值法多信道检测算法。而且当采样点数量增多时，这几种算法的检测性能都有所提高。这是因为，当采样点增多时，由采样协方差所估计得到的协方差矩阵越来越接近统计协方差矩阵，使得算法的准确性得以加强，有利于信道中干扰信号的检测。

图3反映了不同干扰比例下认知跳频多信道频谱检测算法的性能曲线，门限的设定由两种方法完成：平均值法和相邻比值法。当干扰因子ρ＝0.8时，即有80%的信道中存在干扰信号时，相邻比值法的检测性能优于平均值法；当ρ＝0.5时，平均值法的性能又优于相邻比值法；当ρ下降到0.2时，相邻比值法的检测性能又超过平均值法。这就说明，一般情况下宜采用平均值法；当信道环境十分恶劣或者信道环境比较好时，宜采用相邻比值法设定门限值。此外，可以看出，当被干扰的信道数量较大时，两种门限法的检测性能都有所下降，反之，检测性能较好。这是因为，干扰比例的增大会带来两个影响：一是随着被干扰的信道数量的增加，会使得总体检测概率Pdall有所下降；另一方面，由于认知跳频系统总带宽为Wss保持不变，信道受干扰比例的增加会使得每个信道上的干扰功率减小，从而增大干扰检测难度，使得总体干扰检测性能有所下降。

4 结论

本文提出了一种基于统计协方差矩阵的多信道频谱检测算法，首先在发射端发送信号之前，对系统的多个信道同时进行检测，对检测信号采样后计算其采样协方差矩阵，然后求出统计协方差矩阵，接着设定判决门限，最后将统计协方差矩阵的对角元素作为判决量，判断干扰的存在。其中，判决门限的设定有两种方法：相邻比值法和平均值法，并对分别采用这两种方法的多信道频谱检测算法进行了仿真分析。通过仿真分析表明，该算法不仅可以同时对多个信道进行检测，并且可以定位干扰位置，避开存在干扰的频点，从而提高跳频系统的抗干扰能力。同时，两种门限设定方法的检测性能各有优劣，一般情况下宜采用平均值法；当信道环境十分恶劣或者信道环境比较好时，宜采用相邻比值法设定门限值。综合考虑算法的复杂度和实际信道环境，实际应用中一般采用平均值法。

［1］刘先锋.基于认知无线电的跳频系统研究［D］.西安：西安电子科技大学，2009.

［2］刘琪.基于跳频的自适应频谱共享方案［J］.电子学报，2010，38（1）：72－76.LIU Qi.Adaptive spectrum sharing scheme based on FH communications［J］.Acta Electronica Sinica，2010，38（1）：72－76.

［3］Adam Wolisz，James Gross，Daniel Hollos.Double Hopping：A New Approach for Dynamic Frequency Hopping in Cognitive Radio Networks［C］／／Personal，Indoor and Mobile Radio Communications.US：IEEE，2008.

［4］潘启飞.认知跳频传输技术研究［D］.哈尔滨：哈尔滨工业大学，2009.

［5］URKOWITZ H.Energydetection of unknown deterministic signals［J］.Proceeding of the IEEE，1967，55，（4），523－53.

［6］漆渊，彭涛.认知无线电中基于循环平稳特征的频谱感知方法［J］.重庆邮电大学学报（自然科学版），2009，21（3）：353－357.QI Yuan，PENG Tao.Cyclostationarity－based spectrum sensing in cognitive radio［J］.Journal of Chongqing University of Posts and Telecommunications，2009，21（3）：353－357.

［7］Zeng Y H，Liang Y C.Eigenvalue－Based Spectrum Sensing Algorithms for Cognitive Radio［J］.IEEE Trans.Veh.Technol.，2009，57（6）：1784－1793.

［8］Zeng Y H，Liang Y C.Spectrum－sensing algorithms for cognitive radio based on statistical covariances［J］.IEEE Trans.Veh.Technol.，2009，58（4）：1804－1815.

［9］曹开田，王尚.基于RMT的合作频谱感知新算法及其性能分析［J］.计算机应用研究，2011，28（7）：2640－2642.CAO Kaitian，WANG Shang.Novel cooperative spectrum sensing algorithm based on RMT and performance analysis［J］.Application Research of Computers，2011，28（7）：2640－2642.

［10］刘志文.基于特征值的频谱感知算法仿真研究［J］.系统仿真学报，2010，22（12）：2805－2808.LIU Zhiwen.Simulation and analysis of eigenvalue－based spectrum sensing algorithms for cognitive radio networks［J］.Journal of System Simulation，2010，22（12）：2805－2808.

［11］曹开田，杨震.基于最小特征值的合作频谱感知新算法［J］.仪器仪表学报，2011，32（4）：736－741.CAO Kaitian，YANG Zhen.Novel cooperative spectrum sensing algorithm based on the smallest eigenvalue［J］.Chinese Journal of Scientific Instrument，2011，32（4）：736－741.

［12］朱毅超，陆建勋.动态频谱抗干扰系统在部分频带干扰下的性能［J］.电子学报，2011（10）：2331－2337.ZHU Yichao，LU Jianxun.Performance of dynamic spectrum anti－jamming systems under partial－band noise jamming［J］.Acta Electronica Sinica，2011（10）：2331－2337.