基于遗传粒子群混合算法的NURBS曲线降阶*
□ 张 鑫 □ 南 余荣
浙江工业大学 信息工程学院 杭 州 3 10023
在计算机图形和计算机辅助几何设计领域,非均匀有理B样条(NURBS)曲线已经成为设计和描述各种复杂曲线的标准,它能表示所有的自由曲线。由于在不同的数据模型中采用的曲线阶数各不相同,为了提高计算效率以及稳定性,实现不同阶数曲线之间的数据交换和传递,必然要解决其降阶问题。因此,NURBS曲线的降阶问题不仅有着重要的理论价值,而且有着迫切的应用需求。
近几年对NURBS曲线降阶问题有了很多的研究成果,文献[1]采用遗传算法实现一次对NURBS曲线降多阶,得到的曲线为全局最优或次优。文献[2]从最优思想出发,把NURBS曲线的降阶问题转化为求最优问题,并基于微粒子群算法给出了NURBS曲线降阶的一种方法。文献[3]利用NURBS曲线的显式矩阵表示和多项式最佳一致逼近理论,得到了以显式表达的NURBS曲线可退化的充要条件,给出了NURBS曲线降阶的方法。本文提出了基于遗传算法和粒子群算法混合的算法对NURBS曲线实现降阶,采用该算法能够更快速更精确地找到全局最优的降阶NURBS曲线。
1 问题的提出
设:P1,P2, …,Pn为给定的 n 个控制顶点,ω1,ω2,…,ωn为相应控制顶点的权,U={u0≤…≤uk≤…≤un+1≤…≤uk+n}为节点序列,由这些控制顶点、权和节点定义的 k 次(k+1 阶)NURBS 曲线的参数方程为[4]:

其中,Nj,k(u)为 B 样条基函数[5],满足:

实际上NURBS曲线的降阶问题就是要找出另外一条 s(s<k)次 NURBS 曲线:

使 f(u)尽量逼近 f(u),两条曲线的逼近程度可以用其参数方程差的最大值来描述:
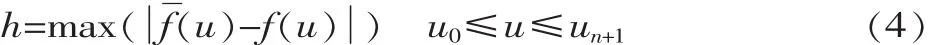
要使降阶后的曲线和原曲线逼近,就要使h的值尽量小。因为NURBS曲线受到控制顶点、权以及节点向量的影响,为了减少计算量,同时又保持曲线的端点不变,在降阶时对降阶后的NURBS曲线的节点向量稍作改动。如果是降一阶,将降阶前节点序列的第一个和最后一个点删除作为降阶后的节点序列,相应的曲线控制顶点也要比降阶前少一个。因此,NURBS曲线降阶问题的实质就是找出一组控制顶点、权以及节点向量,使由它们确定的NURBS曲线尽可能逼近原曲线。所以降阶问题转化为如下带约束条件的优化问题:

式中:R为实数。
2 粒子群算法和遗传算法的基本原理
2.1 粒子群算法
粒子群算法属于迭代算法的一种,从随机解出发,通过迭代寻找最优解,同时通过适应度来评价解的品质。在算法中,设有N个粒子组成一个粒子群,其中Xi(xi1,xi2,...,xin)为第 i个粒子的位置,它是优化问题的一个潜在解;Pi=(pi1,pi2,...,pin) 为粒子 i所经历的最好位置(即具有最好的适应值);Pg(pg1,pg2,...,pgn)为群体中所有粒子经历过的最好位置;Vi=(vi1,vi2,...,vin)为粒子i的飞行速度,对于每一代t,每个粒子第d维(1≤d≤n)的速度和位置根据下列方程更新[6,7]:

式中:ω 为惯性权重;c1、c2为学习因子;rand ()、Rand()为两个在[0,1]范围内独立均匀分布的随机数。
标准粒子群算法的算法流程如下:
1)初始化群体规模为N粒子群,包括每个粒子的位置和速度。
2)计算每个粒子的适应值。
3)对于每个粒子,将其适应值与它所经历过的最好位置pbest的适应值进行比较,如果较好,则将其位置作为它自身当前的最好位置pbest。
4)对于每个粒子,将其适应值与全体粒子所经历的最好位置gbest的适应值进行比较,如果较好,则将其位置作为当前群体的最好位置gbest。
5) 根据方程(6)、(7)对每个粒子的速度和位置进行更新。
6)如果终止条件(通常为足够的适应值或达到一个预先设置的最大代数Gmax)满足则停止,否则转到第二步。
2.2 遗传算法
遗传算法跟其它智能算法一样,也是通过模拟自然进化过程来搜索最优解。它求解问题的基本方法是:从当前种群出发,待优化的目标函数解释为生物种群对环境的适应性,生物个体对应优化变量,利用选择、复制、杂交和变异操作来生成新的种群。重复这个过程,直到出现满足要求的种群或者达到了规定的进化限制。
遗传算法的主要运算过程[8]如下。
1)编码:编码的方法主要有二进制编码、符号编码和浮点数编码3大类。
2)初始群体的生成。
3)适应度值评估监测:适应度函数表明个体或解的优劣性。
4)选择:常用的方法有轮盘赌选择、锦标赛选择、随机竞争等。
5)交换:交换(也叫杂交)操作是遗传算法中最主要的遗传操作。
6)变异:变异可以改善遗传算法的局部搜索能力;维持群体的多样性,防止出现早熟现象。
7)终止条件判断有3种情况:给定一个最大的遗传代数,算法迭代到最大遗传代数时停止;给定问题一个下界的计算方法,当进化中达到要求的偏差时,算法终止;当监控得到的算法再进化已无法改进解的性能即适应度无法再提高时,此时停止计算。
3 遗传粒子群混合算法在曲线降阶中的应用
粒子群算法收敛速度快,但易陷入局部最优;遗传算法把握全局的能力好,但收敛速度慢,本文将遗传算法融入到粒子群算法中,以充分利用各自的优点,形成即收敛速度快、又能收敛到全局最优的算法,并应用于NURBS曲线降阶中。由于遗传算法运算时间长的主要原因是其编码解码操作,本文提出的算法抛弃编码解码,直接对pbest和gbest进行交叉和变异。因为粒子是通过跟踪pbest和gbest来更新自身的速度和位置的,pbest和gbest一旦改变,粒子的速度和位置会跟着改变,而pbest和gbest的变化是通过遗传操作来实现的,遗传操作是一种导向式的操作,它能使pbest和gbest向有利于收敛的方向变化,从而使粒子的速度和位置也向着有利于收敛的方向进行更新。
遗传粒子群混合算法应用于NURBS曲线降阶时,把NURBS曲线的待求解(降阶后的控制顶点、权因子向量以及带点序列)看作是一个粒子,每个粒子的位置为待优化问题中的一个潜在解。此混合算法将在遗传算法的变异和粒子群算法中的学习因子中引入自适应机制,在变异过程中引入自适应的概念即发现算法有可能陷入了局部最优时才进行变异,而平时并不进行变异,以节约运算时间;在学习因子中引入自适应是因为学习因子反映的是粒子的学习能力,学习因子大,粒子的学习能力就强,但在算法的早期粒子需要较强的学习因子以尽快找到全局最优;而在算法后期,粒子的学习因子如果小一些,可以使粒子在全局最优附近进行精细搜索,从而得到尽可能精确的解。c1、c2的更新方式如下:

式中:MaxIter为最大迭代次数,Iter为当前迭代次数。
算法的具体步骤如下。
1) 给出 pi,ωi和 Ti的可行解范围,其中 pi为降阶后的控制顶点分量,ωi为降阶后的权因子,Ti为降阶后的节点序列。为了保证端点的插值性,令:p0=p0,pn-m=pn。
2)确定粒子群算法的种群大小、惯性权重,学习因子,文中选取种群大小Popsize,惯性权重ω=0.675,学习因子 c1、c2根据方程(8)、(9)更新,最大迭代次数MaxIter为 1 000。
3)种群初始化:在解的可行域随机确定400个(可能解)。
4)计算每个粒子的适应度,适应度函数取为:
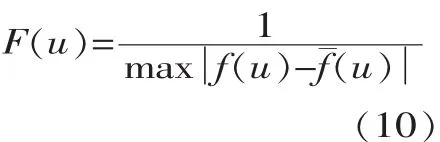

▲图1 四阶降为三阶的NURBS曲线与控制线
5)取适应度高的直接进入下一代,而适应度低的另一部分进入遗传池进行遗传。遗传直接对粒子的pbest进行操作,以避免费时的编码解码操作。
6)更新个体最好位置pbest和群体最好位置gbest。
7) 根据方程(6)、(7)对粒子的速度和位置进行更新,学习因子 c1、c2则根据方程(8)、(9)进行更新。
8)判断种群是否达到最大进化代数,如未达到,则转向步骤3),否则给出最优解和最优目标函数。
4 实验仿真
用MATLAB7.0编程实现此算法。为描述简单,只在平面内画二维图像,即让控制顶点第三坐标轴取零。
设一条4次NURBS曲线,节点序列u={0,0,0,0,0.4,0.7,1,1,1,1},控制顶点 p={(10,10,0),(41,88,0), (84,115,0), (178,9,0), (231,30,0),(290,110,0)},权因子 ω={1,1,1,1,1,1}。对此曲线分别用遗传算法、粒子群算法和遗传粒子群混合算法降一阶所得控制顶点及权因子(见表1),所得曲线及相应的控制顶点与原曲线和控制顶点 (如图1所示),图中折线表示控制多边形,曲线表示NURBS曲线,并对其中部分曲线进行放大。从图1可以看出,用遗传粒子群混合算法降阶后的曲线与原曲线基本重合,降阶效果较遗传算法、粒子群算法更好。
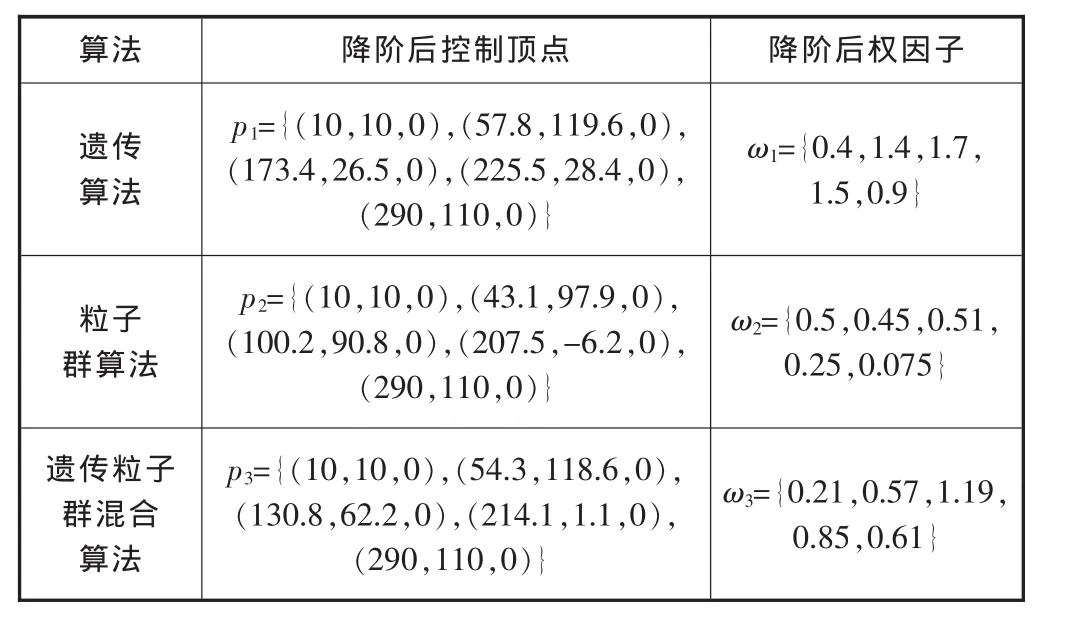
表1 NURBS曲线降阶结果
5 总结
本文利用NURBS曲线的几何性质,并结合遗传算法和粒子群算法,给出了NURBS曲线降阶的一种新方法。利用粒子群算法收敛速度快、遗传算法把握全局能力好的特点,将遗传粒子群混合算法应用于NURBS曲线的降阶中。实验结果表明,本算法能在保留原曲线端点处几何信息的前提下达到较好的逼近精度。本文的思想和方法可以方便地推广到参数曲面上的降阶逼近。
[1] 刘彬.基于遗传算法的NURBS曲线降阶[J].计算机工程,2008,34(14):194-196.
[2] 江明,罗予频,杨士元.基于微粒群算法的有理Bezier曲线降阶[J].计算机应用,2007,27(6):1524-1527.
[3] 程敏,王国瑾.基于显示矩阵表示和多项式逼近论的NURBS 曲线降多阶[J].中国科学(E 辑),2003,33(8):673-680.
[4] 王国勋,王宛山,王军,等.实时快速NURBS直接插补技术[J].中国机械工程,2013,24(5):617-622.
[5] Les Piegl,Wayne Tiller著,赵罡,穆国旺,王拉柱译.非均匀有理B样条[M].北京:清华大学出版社,2010.
[6] A A A Esmin,G Lambert-Toores,A C Zambroni de Souza.A Hybrid Particle Swarm Optimization Applied to Loss Power Minimization [J].IEEE Transactions on Power Systems,2005,20(2):859-866.
[7] D I S Adi,S M B Shamsuddin,S Z M Hashim.NURBS Curve Approximation Using Particle Swarm Optimization[C].2010 Seventh International Conference on Computer Graphics,Imaging and Visualization,Sydney,NSW,2010.
[8] 康宝生,石茂,张景峤.有理 Bezier曲线的降阶[J].软件学报,2004,15(10):1522-1527.

