凸轮检测中的数据处理方法研究

□ 张培硕 □ 韩秋实 □ 李启光 □ 彭宝营

北京信息科技大学 机电工程学院 北京 100192

凸轮轴检测设备精度高，造价昂贵，对于一般小企业很难购入整套设备，而搭建一个比较理想的凸轮轴数据采集机械平台是较容易实现的，再开发出一套算法缜密的数据处理方法，可降低凸轮轴检测的价格，使小公司也能实现检测处理，同时对凸轮轴在线测量及加工过程中的实时反馈系统搭建有重要意义。目前，主流的凸轮轴检测中的数据处理方法，是在采集数据前，先确定测量起始点，测出数据之后直接与升程表相减，得到升程误差，将测得的结果直接画出。此种方法的优点是简单，但可靠性低，基本没有考虑测量误差的影响，是不可取的。基于以上原因，笔者在对凸轮检测过程中数据处理方法深入研究的基础上，提出了一种相对完善的数据处理方法。

1 凸轮检测数据处理实施方案

数据处理就是对数据进行采集、存储、检索、加工、变换和传输，在检测装置测得凸轮数据之后，对数据进行如下处理。

1.1 用滤波法进行数据降噪

由于工业控制对象的环境一般比较恶劣，干扰源较多，如强电磁场干扰、环境温度变化较大等，为了减少对采样值的干扰，提高系统的性能，一般在进行数据处理之前先要对采样值进行数字滤波。所谓数字滤波，就是通过一定的计算程序减少干扰信号在有用信号中的比重。

当采样信号由于随机干扰、误检或者变送器不稳定等原因使检测数据有部分失真时，可以运用程序判断滤波方法，对数据进行滤波降噪处理。其原理是：根据经验确定出两次采样输入信号可能出现的最大偏差ΔT，若相邻两次采样信号差值大于ΔT，则表明该采样信号是干扰信号，应排除；若小于ΔT，则表明干扰不明显，采集到的数据相对可信。此方案具体实施办法就是把相邻两次采样值相减，求出其增量的绝对值，然后与最大允许误差ΔT进行比较，如果小于或等于ΔT，则取本次采样值；若大于ΔT，则仍取上一次的采样值作为本次的采样值，即：

式中：Tn为第n次采样值；Tn-1为第n-1次采样值。

程序判断滤波方法的关键在于最大允许误差ΔT的选取，ΔT太大，干扰就不能有效排除,ΔT太小，又会使某些有用的信号被过滤，使采样效率变低，通常ΔT根据经验数据获得，必要时可由实验得出。

1.2 计算桃尖角度

求凸轮的桃尖是求解凸轮测量起点的角度，是凸轮测量工序中的关键步骤，实际上是指按设计要求求解凸轮最大升程的转角值、求解凸轮零升程点的转角值或求解凸轮升程起始基准的转角值的过程的统称。按设计给出的转角起点，计算出桃尖与转角起点角度的关系，再以起点转角开始对凸轮进行测量，这就解决了凸轮的对正问题。找到桃尖就可以找到其它相应的点，桃尖转角通用计算公式为：

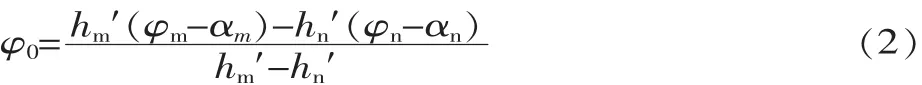
式中：φm、φn分别为左右侧升程变化率最大的点所对应的角度；hm、hn分别为左右升程最大点的升程变化率；φ0即为桃尖转角值。

1.3 二次消差

找到桃尖之后，就可以用实测数据建立起实测凸轮轮廓。对于理想凸轮，从动件在基圆上任意采样点ki的相对位移误差ΔK都是相等的，见图1，设凸轮检测起点为A，凸轮非基圆轮廓上一点k，此点相对于起点A使测头发生的相对位移值为ΔS,又设该点的绝对升程值（相对于基圆）为Lk，则：

对于非理想凸轮，由于基圆误差及跳动误差等影响，ΔK在每个采样点ki上的值不相等，为了让ΔK具有代表性，进一步获得理想的消差效果，取：

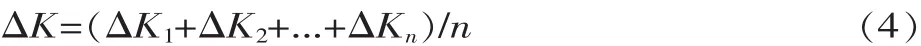
将式（4）代入式（3），可得：

用式（5）矫正过的实测值来求升程误差，结果的可信度将进一步提高。

▲图1 二次消差原理图

1.4 升程误差计算

凸轮升程误差是实测的升程值与对应点的理论升程值之差，此时将实测数据与理论数据对应相减，得出升程误差值是不科学的，因为实测位置与理论位置一般不会一一对应，都会存在一个小夹角，为解决此问题，用曲线拟合的方法来调整对正。曲线拟合的思想是根据一组二维数据，确定一个一元函数y=f（x），使这些点与曲线总体来说尽量接近，曲线拟合的目的是根据实验获得的数据去建立因变量与自变量之间有效的经验函数关系。实验证明，最小二乘法的拟合效果已经能够达到精度要求，将角度值代入拟合曲线方程，即可求得角度对应的升程值，两者相减即是升程误差值。

2 应用实例

被测量的凸轮是在新研制的车磨复合机床上加工的，基圆半径为18.237 mm，数据是应用广州威尔逊公司生产的L系列凸轮轴检测仪采集得到，一圈共360个采样点，采集间隔为一度。

2.1 用滤波法进行数据降噪

实际测量中，取ΔT=0.02 mm，滤波前后的对比见图2，几处有明显突变的点被滤掉。

2.2 计算桃尖角度

▲图2 滤波前后局部曲线对照

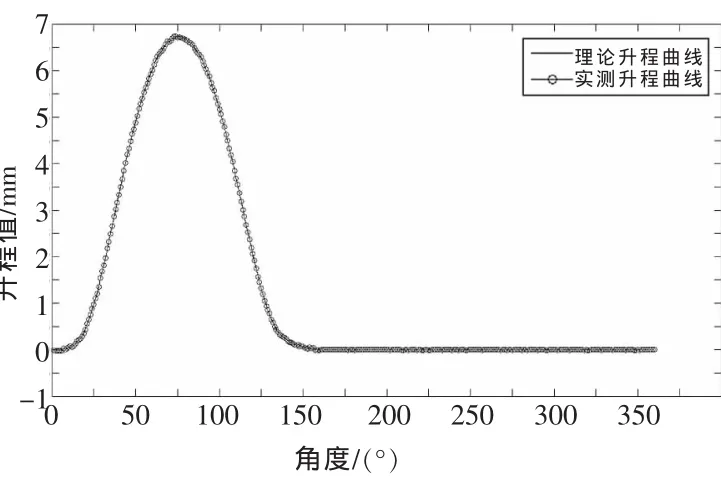
▲图3 理论升程曲线与实测升程曲线对比图

▲图4 4个不同局部放大效果图

将升程表导入MATLAB，用软件工具箱编定的程序即可算出：

φ0=-1.837 即 ：φ0==-105.292 5°，φ0=105.292 5°

2.3 二次消差

用式（5）计算消差，得 ΔK=0.8 μm，误差值较小，本次实例中二次消差效果不明显，其原因是，本实例处理的数据，采集于专业凸轮轴检测仪，它的机械结构相对比较完善，采用气浮顶尖，来自自身的误差较小。

2.4 升程误差计算

采用最小二乘法，在凸轮非基圆段作曲线拟合（次数取为30次时，误差率为0.001 mm），拟合后将各角度值输入，重新得到一组升程数据，此数据与实测数据相减，部分结果见表1。以曲线形式给出，见图3。具体位置误差情况，可用局部放大功能，见图4，它是曲线在不同位置的局部放大图，纵坐标方向精度依次为0.5 mm、0.2 mm、0.1 mm、0.001 mm。

表1 部分升程误差对比表

3 结论

对于传统的凸轮轴数据处理方法，缺少程序滤波处理或曲线拟合处理步骤，数据处理结果的精准性会降低，为了让数据处理方法更加完善，将滤波、曲线拟合思想融入数据处理方法，本文对凸轮轴检测过程中数据处理原理进行了深入研究，借助MATLAB工具，编写出了一套基于程序判断滤波及最小二乘曲线拟合的处理程序，运算简单方便，计算精度较高，考虑到了采集过程中的突变误差点，采集系统本身引入的误差及角度精准对正问题，对凸轮轴廓形误差检测研究具有重要意义。

［1］ Yi Bao Yuan，Yu hua Wang.Development of Camshaft Journals Multi-parameters Measuring Inst-rument［C］.Pervasive Computing Signal Processing and Applications （PCSPA）,2010 First Inte-rnational Conference on，Sept.2010:1285-1289.

［2］ Li Juan Zhong，Jing Lin Tong.Research and Implementation of Automatic Camshaft Measurement Technology ［J］.Key Engineering Materials，2010（12）:297-301.

［3］ 李长星，刘兴富.发动机凸轮轴检测方法综述［J］.计量技术，2005（8）：27-30.

［4］ 刘兴富.凸轮测量借助计算机快速找“桃尖”方法［J］.金属加工（冷加工），2009（4）:52-55.

［5］ 缪雪龙，张毅华.数值计算在凸轮型线分析中的应用［J］.内燃机燃油喷射和控制，2000（1）：36-38.

［6］王忠，郁鼎文，张玉峰，等.平面凸轮轮廓线检测数据处理方法研究［J］.制造技术与机床，2004（7）：53-55.

［7］ 孙恒，陈作模，葛文杰.机械原理（7 版）［M］.北京:高等教育出版社，2005:160-164.

［8］ 李庆扬，王能超，易大义.数值分析［M］.北京:清华大学出版社，2008：73-78.