基于灰色理论的汽车销售量预测研究

□黄琦

武汉理工大学 机电工程学院 武汉 430070

近年来，随着我国汽车市场的高速增长，汽车产能急速扩张，国内汽车市场风云变幻，如何对汽车的销售量作出准确的预测和定位，是整个汽车市场需要解决的问题。各大企业为了使其经济活动达到预期的目的，都需要通过分析历史数据，对汽车销售量进行预测，以利于制定营销战略和生产计划。因此，也向汽车生产企业提出了问题和挑战：如何对汽车的销量作出准确的预测，以此来指导企业的生产规划，把握未来汽车市场的发展趋势。

尽管目前汽车销量预测方法很多，但由于社会各方面经济因素的影响，我国的汽车产销量正处于不稳定的发展阶段，统计数据不具有典型的概率分布特性，灰度较大，套用传统的预测方法并不合理。为此，本文提出了运用灰色理论预测模型来预测我国年汽车销售量的发展趋势。

1 灰色系统预测

灰色系统理论由中国学者邓聚龙教授于1982年创立，它是一种研究少数据、贫信息不确定性问题的新方法。灰色系统是介于白色系统和黑色系统之间的一种系统。白色系统，即信息完全明确的系统，黑色系统是内部信息一无所知的。而灰色系统，其内部部分信息明确、部分信息不明确。因此，灰色预测就是对这种既含有已知信息又含有不确定信息的灰色系统进行预测。

灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来的发展趋势。其用等时距观测到的反应预测对象特征的一系列数量值构成灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。

灰色预测是基于灰色模型（GM）作出的定量预测，按照其功能和特征可分成数列预测、区间预测、灾变预测、季节灾变预测、波形预测和系统预测等几种类型。其中，数列预测是对系统变量的未来行为进行预测，其预测的结果是该变量在未来各个时刻的具体数据。本文基于灰色理论GM（1,1）模型，采用数列预测法，以我国2004～2011年汽车的销售量统计数据为基础，对未来几年汽车年销量进行预测，从而提供有效的参考信息。由于汽车年销量为非负数列，所以它是一个灰色系统，建立GM（1,1）预测模型。

表1 中国汽车年销量（2004～2011年）

表2 汽车年销量预测模型预测值与实际值的比较

2 我国汽车年销量灰色预测模型GM（1,1）的建立

数列预测的基础是基于累加生成数列的GM（1,1）模型。GM（1,1）模型是常用的一种灰色模型，由一个单变量的一阶微分方程构成，主要用于中长期预测。

设 X（0）=［x（0）（1），x（0）（2），．．，x（0）（n）］是一组所要预测的变化量的原始数据，一般而言，这是个不平稳的随机数列。对于这样一个随机数列，如果趋势无规律可寻，就无法用回归预测法对其进行预测。

但如果对该数列做一次累加生成处理，即：

……

可得 X（1）=［x（1）（1），x（1）（2），x（1）（3），．．，x（1）（n）］

建立关于 x（1）（n）的一阶线性白化微分方程：+ax（1）=b，利用最小二乘法求解参数 a 和 b，得［a，b］T=（BTB）-1BTY。

其中：

则 X（1）的灰色预测 GM（1,1）模型的时间响应函数为：

其实际预测值可由下式得出：

根据中国汽车工业协会统计，将2004～2011年的我国汽车年销量数据设定为预测模型的原始数据，其统计数据见表1。此数组为：

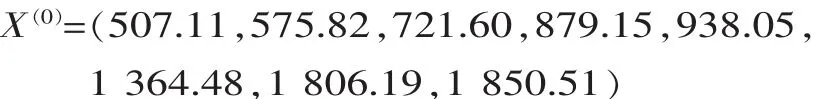
将此数组数据进行累加，得到具有更强规律性的数组为：

根据公式，可确定系数向量：

因此，我国汽车年销量预测模型可确定为：

3 我国汽车年销售量预测模型的检验和预测

从预测模型基本公式中，得到的是第k个数列的累加值，将相邻的两个累加值相减，则可以得到第k+1个数列的预测值。即：

为检验所建灰色模型的精度，将k=0、1、…、7代入模型，计算出2004～2011年我国汽车年销量的预测值，与原统计数据进行对比检验分析，比较结果见表2。

从表中的残差检验数据可以直观地看到，模型预测值与实际值相对误差较小，吻合较好。

由表2中的数据可计算出平均相对误差：

平均相对误差也较小，符合残差合格模型。

检验均方差比值C：

表3 灰色预测精度检验标准表

由于本文选取了2004～2011年间的8个销售量数据作为基础数据，因此将k=8、9…分别代入式 （3）和（4），可以得到我国2012年及以后年份的汽车销售量的预测值。根据所建模型，对2012年的汽车销售量进行了预测，预测值为2 403.82万辆。

4 结束语

基于灰色理论GM（1,1）模型，依据我国近年汽车销售量统计数据，对未来汽车年销售量进行预测。从预测效果上看，预测值与实际值比较接近，表明该模型在汽车年销量预测研究上具有一定的参考价值。但预测模型是对数据未来趋势的一种定量化描述，GM（1,1）模型只是用一个灰色作用量来综合考虑各种因素对需求量的影响，预测结果相对粗略，而且实际对未来的预测与国家政策、世界经济形势等大环境因素息息相关，因此，模型预测只能作为参考。

［1］ 刘思峰.灰色系统理论及其应用［M］.北京：科学出版社，2008.

［2］ 邓聚龙.灰色理论基础［M］.武汉：华中科技大学出版社，2002.

［3］ 田冲，薛春善.灰色理论在大学生生活费用预测中的应用［J］.安顺学院学报，2008，10（5）：1-1.

［4］ 赵艳妮，郭华磊.灰色理论GM（1,1）模型在农民人均收入预测中的应用［J］.现代电子技术，2010（13）.

［5］ 邓绍云，邱清华.灰色理论在区域水资源耗用量预测中的应用研究［J］.红水河，2011（1）.

［6］ 蔡家明.灰色系统模型在汽车市场需求预测中的应用［J］.上海工程技术大学学报，2003（3）.

［7］ 胡坤.灰色预测评价方法与应用研究［D］.南京：南京航空航天大学，2004.

［8］ 陈欢.灰色理论在汽车销售预测和投资决策中的应用研究［D］.合肥：合肥工业大学，2008.

［9］ Deng J.Grey System FundamentalMethod ［M］.Wuhan:Huazhong Institute of Technology Press，1987.