二元会话类型系统中演进特性研究*
钟发荣,杨振国
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引言
网络技术的快速发展促进了分布式的应用和服务.在以通信为中心的程序设计中,通信协议较为复杂,涉及大量的状态和状态迁移,它们可由不同的消息类型产生.在实现分布式应用系统的进程时,必须保证进程间所传递的消息的结构和序列与通信协议保持一致.
会话类型理论[1-3]是基于Pi-演算[4-5]的一种形式化方法,能够结构化交互和解释通信行为.进一步地,会话类型的子类型[6]能使会话参与者,即使它们分别遵循不同的协议描述,仍能相互兼容地通信,从而增强了会话类型理论的表达力.然而,程序员很难保证在准确、严格的时间点发送或接收消息.为了处理这个问题,Dezani-Ciancaglini 等[7]在MOOSE 语言中定义了演进特性,即通信会话一旦开始,合式进程在会话通道上不会发生死锁.
本文分析了二元同步会话类型系统中进程通信可能产生的死锁情形,并结合会话类型的子类型和松弛对偶关系,给出了类型一致性法则,同时证明了当前二元同步会话类型系统保持演进特性.
1 会话类型理论基础
1.1 会话类型
实现涉及复杂通信序列的应用程序时,必须确保消息的序列和结构与通信协议保持一致.然而,标准的编程语言并不支持这一验证.一种主流的验证方法是将通信行为先抽象为类型,然后利用这些类型检查应用程序中实际使用的通道,这就是会话类型的思想.例如,在客户机-服务器系统中,服务器端的类型为begin.?[int].![bool].end,表示服务器首先接收一个整型值,然后返回一个布尔值,从而结束通信.假设服务器提供的服务分别为求平方和退出,与客户机端在会话通道x 上发生通信,会话通道的2 个端口分别记为x+和x-,用来表达进程中会话发生的位置,这里+和-为会话通道的极性.通常地,用x+表示服务器端,x-表示客户机端,2 个端口所对应的会话类型分别为Server1和Client1.例如:

很显然,Server1| Client1归约不存在任何问题.&{…}是分支构造子,表示服务器的外部选择功能,sqr 和quit 是2 个标号,每个标号有一个后继类型,用于表示消息序列,?表示输入,!表示输出,⊕{…}是选择构造子,表示客户机的内部选择功能.
1.2 会话类型子类型
上例中的服务器端升级后,原先通信协议中的消息序列已经发生了改变.如果此时客户机端进程的消息序列保持不变,那么两者又如何继续通信呢?例如,服务器端消息序列由原来的Server1升级到Server2,即

而客户机端仍然保持消息序列Client1不变,Server2| Client1归约如何进行?Gay 等[6]通过定义子类型的概念解决了这个问题:即在服务器端进程升级后、原先的协议和会话类型已经改变的条件下,服务器端仍能够兼容原来的客户机进程,使两者安全地通信,但要求输入、分支和后继会话类型具有协变性,输出和选择会话类型具有逆变性(?[int]≤?[real],![real]≤![int]).例如,服务器端的会话类型从?[int]升级到?[real],表明服务器端当前期待接收一个实型值.由于子类型的定义,服务器端也能够接收诸如整型等类型的值,从而在相同的通道中,2 种不同会话类型相互兼容.升级后的服务器端与保持不变的客户机端仍可以安全地通信.
会话类型子类型能够解决服务器端升级的问题.利用传统对偶规则,可以推断与升级后的服务器相匹配的客户机端的会话类型,直接得到Client2,即

事实上,客户机端的类型仍然保持Client1不变.由于引入了子类型概念,使得Server2和Client1在通信过程中不会产生错误,因此定义了松弛对偶关系概念,将Server2和Client1也视为对偶的,这样不仅进一步提高了系统的灵活性,也有助于演进特性的研究.
1.3 演进特性
首先,通信通道被区分成共享通道和活动通道2 种,其中共享通道用于通信时建立连接.连接建立以后,约束通道名字由活动通道替换,这里活动通道是新私有名字.演进特性要求类型系统中进程通信一旦发生,合式进程在通道上不会发生死锁.演进特性能确保在运行前发现通信进程中所隐含的错误,以及通信归约的安全性,是各种应用程序安全的基本要求.为了解释此通信安全问题,考虑下面的客户机-服务器交互模式的进程,假设服务器端进程为

首先通过共享通道a 接收一个活动通道,然后活动通道替换x 并执行如下通信:输出一个整型值,输入一个整型值,输出一个字符串,最后继续P1进程.客户端进程为

请求共享通道a 上的会话通信,然后通过活动通道x 执行与服务器端类型对偶的动作.一旦会话建立,很显然,活动通道上的通信总能继续.
上面例子仅局限在2 个参与者在一个会话中的交互.实际上,在Web 服务通信中,在2 个甚至多个参与者中建立多个会话的情况是很常见的.这种情况下,当2 个或多个会话交织时,安全性很容易被破坏,最简单的例子如下:

由x 和y 替换的活动通道导致了死锁.尽管在会话类型系统中,客户机端进程上的2 个通道分别为x 和y,分别考察2 个进程,它们的结构是正确的且是可类型指派的,但是在活动通道上的通信不能确保演进特性.
2 二元会话类型系统
2.1 语法和概念
下面首先定义消息类型和会话类型,然后定义松弛的对偶关系.
类型的语法如图1 所示.假设端口x+的会话类型为S,那么,端口x-的会话类型则为,称其为类型S 的对偶.图2 定义了非递归类型的松弛对偶关系,对于递归类型,给出余归纳的定义.

图1 语法

图2 松弛的对偶关系
定义1 一个关系R1⊆Type×Type 被称为松弛的对偶关系,如果满足下面条件:
1)如果unfold(T)=?[T].S1且unfold(U)=![U].S2成立,那么(S1,S2)∈R1且U≤cT 一定成立;
2)如果unfold(T)=![T].S1且unfold(U)=?[U].S2成立,那么(S1,S2)∈R1且T≤cU 一定成立;
3)如果unfold(T)=&{l1:S1,l2:S2,…,ln:Sn}且unfold(U)=⊕{l1:V1,l2:V2,…,lm:Vm}成立,那么(Si,Vi)∈R1一定成立;
4)如果unfold(T)=⊕{l1:S1,l2:S2,…,lm:Sm}且unfold(U)=&{l1:V1,l2:V2,…,ln:Vn}成立,那么(Si,Vi)∈R1一定成立;
5)如果unfold(T)=end 成立,那么unfold(U)=end 一定成立.
定义2 余归纳的松弛对偶关系⊥c由T⊥cU 定义,当且仅当存在一个类型模拟R1使得(T,U)∈R1成立.
2.2 进程
进程的语法如图3 定义,其中大多数语法是标准的.名字是极化的,表示为x+或x-,或直接用xp表示.其中:p 表示可选择的极性;0 是空进程,表示该进程不做任何动作;|是并行复合.

图3 进程
2.3 会话类型的子类型指派
非递归会话类型的子类型指派规则如图4 所示,其中有界类型变量X1,X2,…,Xn都满足环境△=L1≤X1≤U1,L2≤X2≤U2,…,Ln≤Xn≤Un.对于递归会话类型的子类型,给出余归纳的定义.

图4 子类型指派
定义3 一个关系R2⊆Type×Type 被称为松弛的对偶关系,如果满足下面条件:
1)若unfold(T)=?[T].S1且unfold(U)=![U].S2成立,则(S1,S2)∈R2且(T,U)∈R2一定成立;
2)若unfold(T)=![T].S1且unfold(U)=?[U].S2成立,则(S1,S2)∈R2且(U,T)∈R2一定成立;
3)若unfold(T)=&{l1:S1,l2:S2,…,ln:Sn}且unfold(U)=⊕{l1:V1,l2:V2,…,lm:Vm}成立,则(Si,Vi)∈R2一定成立;
而据宫宝田弟子回忆,师父给许世友展示了刀法,水泼不进,而许世友也展示了刀法,快准狠绝,师父给许世友展示了轻功,警卫用枪都打不到他,而许世友则展示了暗器飞蝗石的绝技,用石子儿打中了师父的毡帽。
4)若unfold(T)=⊕{l1:S1,l2:S2,…,lm:Sm}且unfold(U)=&{l1:V1,l2:V2,…,ln:Vn}成立,则(Si,Vi)∈R2一定成立;
5)若unfold(T)=end 成立,则unfold (U)=end 一定成立.
定义4 余归纳的松弛对偶关系≤c由T≤cU 定义,当且仅当存在一个类型模拟R2使得(T,U)∈R2成立.
3 二元同步会话类型系统的通信安全性
3.1 通信中的死锁情形

注意上述2 个进程所遵循的协议中的消息类型是不同的.由于引入了会话类型的子类型概念,两者通信归约不会产生错误,松弛的对偶关系很好地解决了此类问题.
例2(类型一致性) 尽管引入了会话类型的子类型,然而2 个进程所遵循的协议并不总是相互兼容的.例如:

其中,y?[int]和y![real]类型不兼容,P2| Q2不能继续下去.为了处理这种不当的通信行为,Acciai等[8]将类型一致性引进到会话类型理论中.进一步,结合会话类型的松弛对偶关系,给出了新的定义,作为结果,认为P2和Q3符合类型一致性法则.其中

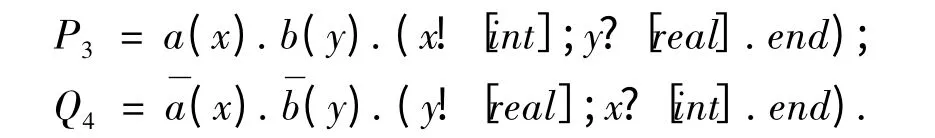
上述2 个进程中,每个进程有2 个共享通道a 和b,分别限制了x 和y 两个活动通道,2 个进程使用活动通道的顺序恰好相反,在同步通信中P3| Q4可导致死锁,此情形在类型一致性法则的定义中得到了解决,它允许进程P3与进程Q5等并行复合.其中

例4(双线性条件) 设进程P4和Q6为:

P4| Q6不能完成通信,双线性条件阻止了此类情形的发生.双线性条件是指有且仅有2 个进程包含相同名字的活动通道.
3.2 演进特性的保持
定义5(演进特性) 称进程P 保持演进特性,当P→P′蕴含要么P′中不包含活动通道,要么Q/→,使得P′ | Q→且P′ | Q 是合式的.
若一个进程P 不死锁,则它能保持演进特性,而某些“坏”形式的进程可能产生死锁.不可归约进程,如果能与其他不可归约进程Q 交互,那么它也保持演进特性.下面给出二元同步会话中的类型一致性法则.

法则1 对于发生在二元同步会话中的通信进程,所有会话类型必须满足如下要求:
1)共享通道名字是自由的;
2)进程两端的活动通道上的端口满足双线性条件;
3)相同通道名字的2 个端口满足类型一致性法则.
定理1(演进特性) 二元同步通信中,如果客户机-服务器交互进程P|Q 满足上述法则,那么P|Q保持演进特性.
证明 假设P0=P | Q 是一个进程,并且P0→*P1,考虑P1的如下3 种可能情形:
1)P1不包含活动通道,或者P1→P′,则P1直接保持演进特性.
2)P1是不可归约表达式,其前缀动作是自由共享通道a 上的接收或发送动作.根据松弛对偶关系的定义,总能建立一个不可归约表达式Q2作为共享通道a 上的请求进程,这也是不能将所有不可归约表达式视为死锁的原因.即使一个不可归约的表达式P1,只要它能够与某个进程Q2进行并行复合,并且使得P1| Q2是合式的,那么该表达式保持演进特性.
3)P1的前缀动作在共享通道上既不包含接收也不包含发送动作,但包含活动通道kp.由于共享通道满足双线性条件和类型一致性法则,所以kp一定会在P1中发生,这意味着它与P1能够归约的情形相同.
4 结论
本文提出了保持演进特性的二元同步会话类型系统,该类型系统确保一旦会话开始,参与者能够完成所有通信动作而不会陷入死锁状态.为了确保当前类型系统保持演进特性,本文分析了二元同步会话类型系统中进程之间通信可能产生的死锁情形,并结合会话类型的子类型和松弛对偶关系定义了类型一致性法则,最后证明了当前类型系统的演进特性.
[1]Honda K.Types for dyadic interaction[C]//Eike Best.Proceedings of the 4th International Conference on Concurrency Theory (CONCUR′93),Lecture Notes in Computer Science 715.Berlin:Springer-Verlag,1993:509-523.
[2]Takeuchi K,Honda K,Kubo M.An interaction-based language and its typing system[C]//Halatsis C,Maritsas D,Philokyprou G,et al.Proceedings of the 6th International PARLE Conference on Parallel Architectures and Languages Europe (PARLE′94),Lecture Notes in Computer Science 817.Berlin:Springer-Verlag,1994:398-413.
[3]Honda K,Vasconcelos V,Kubo M.Language primitives and type discipline for structured communication-based programming[C]//Chris Hankin.Proceedings of the 7th European Symposium on Programming(ESOP′98),Lecture Notes in Computer Science 1381.Berlin:Springer-Verlag,1998:122-138.
[4]Sangiorgi D,Walker D.The π-calculus:a theory of mobile processes[M].Cambridge:Cambridge University Press,2003.
[5]Milner R,Parrow J,Walker D.A calculus of mobile processes,I and II[J].Information and Computation,1992,100(1):1-77.
[6]Gay S,Hole M.Types and subtypes for client-server interactions[C]//Swierstra S.Proceedings of the 8th European Symposium on Programming(ESOP′99),Lecture Notes in Computer Science 1576.Berlin:Springer-Verlag,1999:640-640.
[7]Dezani-Ciancaglini M,Mostrous D,Yoshida N,et al.Session types for object-oriented languages[C]//Thomas D.Proceedings of the 20th European Conference on Object-Oriented Programming (ECOOP′2006),Lecture Notes in Computer Science 4067.Berlin:Springer-Verlag,2006:328-352.
[8]Acciai L,Boreale M.A type system for client progress in a service-oriented calculus[J].Lecture Notes in Computer Science,2008,5065:642-658.

