基于单帧图像的超分辨率算法*
贾 泂,付芳梅,郑忠龙,赵建民,郭 丽,张海新,俞牡丹
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引言
图像的超分辨率技术在视频、遥感、医学和安全监控等领域具有十分重要的应用,同时也逐步扩展到其他各个领域.随着稀疏编码与压缩传感理论的逐步发展,图像的超分辨率算法已经成为研究热点之一.图像的超分辨率(super resolution,SR)是指由一幅低分辨率图像(low resolution,LR)或图像序列恢复出高分辨率图像(high resolution,HR).但是,SR 问题是一个不适定问题,只有在合理的假设和先验知识条件下,SR 问题才是可逆的.在图像处理领域中,已经涌现了诸多图像的超分辨率算法[1-4].这些算法分为2 类:一类是基于重建的算法;另一类是基于示例学习的算法.基于重建的算法的主要缺点是:如果没有足够的约束条件或超分辨率的倍数过高,得到的图像的效果明显下降.基于示例学习算法就能较好地克服这一缺点,它先学习低分辨率图像块与高分辨率图像块之间的函数关系,然后通过这种关系得到相应的高分辨率图像.
基于示例学习的SR 算法可分为基于最近邻的和基于回归的算法.基于最近邻算法得到的图像在视觉效果上比较差.因此,学者们提出了基于回归算法,该算法首先学习从低分辨率图像块映射到高分辨率图像块的函数.文献[1-5]的算法都是基于训练样本库来学习回归函数,这样的算法对于大样本训练图像需要花费大量的时间,并且实验结果也依赖于对样本库的选择.因此,研究只基于低分辨率图像本身来重建高分辨率图像的算法更有意义.
由文献[6-7]知,自然图像具有冗余性与自相似性,同一尺度或不同尺度同场景的图像块都重复出现很多次.本文结合基于示例学习算法与图像的自相似性,提出一种新的图像超分辨率算法,仅基于单幅低分辨率图像本身,没有额外的样本库.实验结果验证了本文算法的优越性,此算法在保证超分辨率图像质量的前提下,克服了对样本库的依赖性.
1 R-KSVD 算法
近几年来,冗余字典算法的研究都基于一种特征空间,而本文算法使用Guided 滤波[8]、一阶导数和二阶导数算法提取图像的2 种特征,得到更加全面的信息.本文算法具体描述(R-KSVD 算法)如下:
输入:字典初始值D0,样本向量y,非零元个数L,最大值相似度s=0.9;
输出:α*为稀疏度为L 的系数矩阵α 的近似值,训练后的字典D;
初始化:初始字典D0,余量e0=y,索引集Δ0=Ø,迭代次数t=1;
R-KSVD 算法主要分为2 步:
1) 稀疏分解:固定D,使用R-OMP 算法估计系数矩阵α;
R-OMP 算法:重复执行步骤1 到步骤5,直到收敛:
步骤1:从D 的所有列与余量e 的内积中找到最大值相似度大于s 所对应的D 的列数,从中随机选出dj,然后通过最小二乘法确定此时的稀疏系数的索引λ;
步骤2:更新索引集Δt=Δt-1∪{λ},字典子集Dt=[Dt-1,dj];

步骤5:若t >L,则输出α*并停止计算.否则继续步骤1.
2) 更新字典阶段:使用SVD 同时更新一次更新字典的每个原子和其相应的非零系数,使得损失函数最小.
冗余字典的学习主要是采用迭代模式交替更新α 和D.字典学习的第1 阶段将D 固定,求出最优系数矩阵α;第2 阶段通过更新后的α,训练得到新的字典~D.如此反复迭代几次即可得到优化的D 和α.大量的字典学习算法已被应用于图像超分辨率领域中[9-10].在字典的更新算法中,K-SVD 的使用较为广泛.K-SVD 运用SVD 每次更新一个原子(即字典的一列)和其对应的稀疏系数,直到所有的原子更新完毕为止,重复迭代几次即可得到优化的字典和稀疏系数.

然而,每次对内积最大列的相应系数进行更新,不一定能得到最优的结果.为了解决这一难题,本文对OMP 算法进行了松弛,提出了一种新的更新系数矩阵的算法Relaxation OMP(R-OMP).首先定义了s表示相对于内积最大列的一个度(本文设为s=0.9),然后随机选择内积最大值相似度大于s 的列,对其相对系数进行更新.本文训练字典算法,第1 阶段使用R-OMP 算法进行稀疏表示,并把这种算法称为松弛的K-SVD 算法,即R-KSVD.由R-KSVD 算法,可进一步了解本文所提的算法.
2 基于单帧图像的超分辨率算法
本文主要研究仅基于一幅低分辨率图像的超分辨率算法,与传统的基于示例的学习算法相比,本文算法不再借用额外的样本库来学习低分辨率图像到高分辨图像的映射关系,而是根据自然图像的自相似性与冗余性[6-7],仅从一幅低分辨率输入图像中挖掘这一函数关系.
仅基于一幅图像的超分辨率可理解为输入一幅低分辨率图像Y,在没有任何额外信息的情况下,输出一幅同样场景的高分辨率图像X.另外,超分辨率后的图像X 应该与输入图像Y 保持一致,即低分辨率图像Y 可以看作是超分辨率图像X 经过模糊和下采样的图像,即

式(1)中:H 表示模糊算子;Sd表示下采样算子.
图像的超分辨率问题是一个不适定问题,这是因为满足约束(1)的高分辨率图像X 不是唯一的.只有在合理的假设和先验知识情况下,图像的超分辨率问题才可以求解.由于字典D 是冗余的,因而所有的高分辨率图像块x 都能通过Dh∈RN×K进行稀疏表示,即

然后将根据低分辨率图像块重建高分辨率图像块.本文使用R-KSVD 算法联合训练低分辨率图像块字典Dl和高分辨率图像块字典Dh.在得到Dl与Dh的前提下,首先对提取特征过的低分辨率图像(梯度图)进行适当的区块划分;然后,利用低分辨率图像字典Dl对每一个梯度图内的图像块y 进行稀疏表达,可得到如下模型:
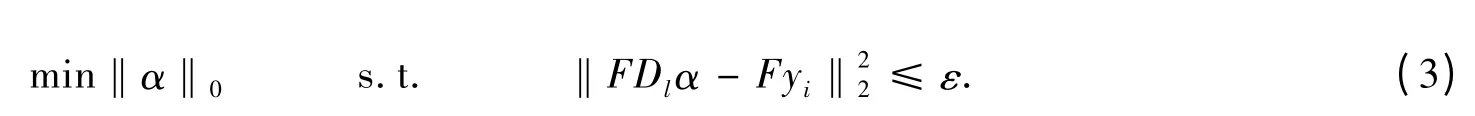
本文算法直接作用于图像的特征域,这里F 是特征提取算子.本文使用Guided 滤波[8]、一阶导数和二阶导数算法提取图像的2 种特征,得到更加全面的信息.
求解式(3)是一件很困难的事.但是最新研究成果表明,只要系数向量α 足够稀疏,式(3)就可以转化为如下模型:
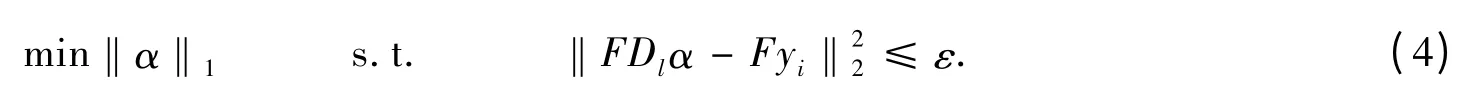
应用拉格朗日寻优法,式(4)又等效于以下优化目标函数:

参数λ 用来平衡优化目标中对系数稀疏性的要求和稀疏表达结果及真实低分辨率图像块y 的接近程度.为了充分利用相邻图像块具体一致性的信息,本文在稀疏表达图像块时采用了从左到右、从上到下的扫描方式.
受近年信号稀疏理论的启发[1],低分辨率图像块和高分辨率图像块相对于字典Dl和Dh,具有大致相同的稀疏表示.给出低分辨率和高分辨率图像块对P={xh,yl}i,其中{yl}i表示低分辨率图像的特征块,{xh}i表示对应的高分辨率图像块.为了保证2 个字典的一致性,联合训练字典Dl和Dh,即
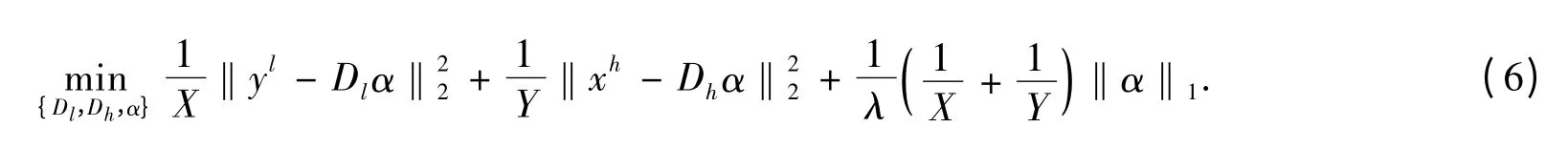
式(6)中,Y 和X 分别表示低分辨率特征和高分辨率图像块合成向量后的维数.式(6)也可以写成
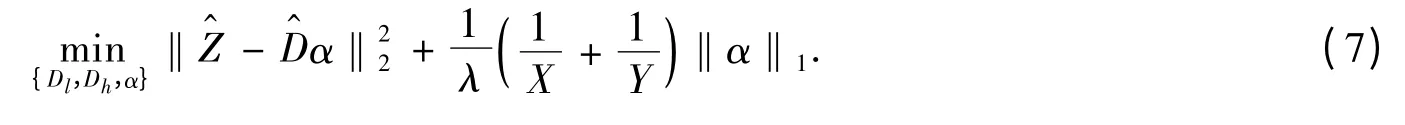
式(7)中,
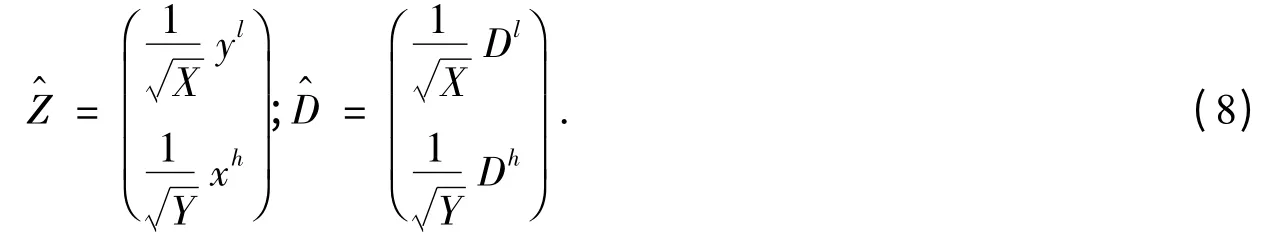
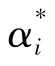
3 后项处理算法
接下来主要讨论基本的后项处理算法(IBP).尽管IBP 算法可以有效地缩小余量且得到不错的效果,但是处理过程中没有考虑边缘信息.笔者在后项处理过程中使用Guided 滤波,更好地估计高分辨率余量图像和恢复边缘信息.这个算法的具体描述如图1 所示.
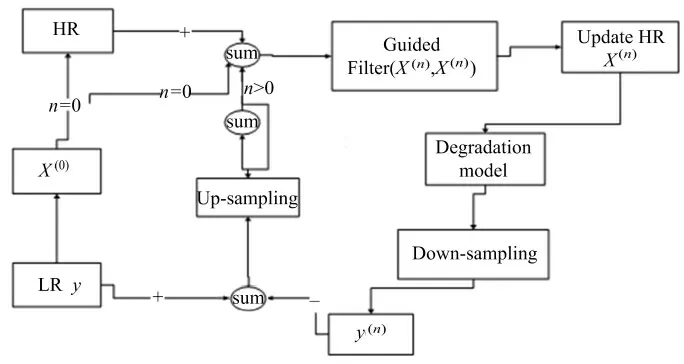
图1 后项处理的过程
第n 次迭代高分辨率图像的余量如下:
1)计算相对于低分辨率图像的误差

2)更新高分辨率图像

式(10)和式(11)中:r 是窗口的半径;γ 是调整参数;4 是超分辨率图像的倍数;X(n)是第n 次超分辨率后的图像.重复此过程直到满足评判标准为止.
4 实验结果
设实验中测试图像的超分辨率倍数为4.实验参数:最大值相似度s=0.9;窗口半径r=2;调整参数γ=0.01;稀疏参数λ=0.01.先用Guided 滤波、一阶导数和二阶导数算法提取低分辨率图像的2 种特征,然后基于输入图像本身从不同尺度和不同方向生成训练字典所需的数据库[6].低分辨率特征块的大小为2 ×2,高分辨率图像块大小为8 ×8,使用R-KSVD 算法联合训练大小为1 024 的字典Dl和Dh.
对于彩色图像,因为人的视觉对光最为敏感,所以只考虑亮度通道,其他2 个通道(Cb,Cr)使用Bicubic 插值算法进行超分辨率.选取的低分辨率图像如图2 所示,超分辨率测试图像分别用了最近邻插值算法(NN)、Bicubic 插值算法(BC)以及本文算法.高分辨率图像的性能指标主要从RMSE(Root Mean Square Error)和SSIM(Structural Similarity)[10]2 个方面进行比较.从表1、表2 和图3~图6 可见,本文的超分辨率算法比其他算法更加优越.
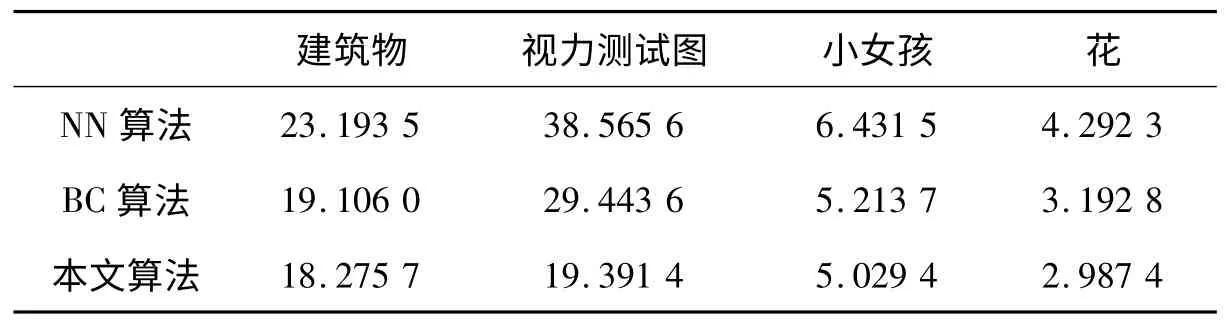
表1 实验结果比较(RMSE 指标)
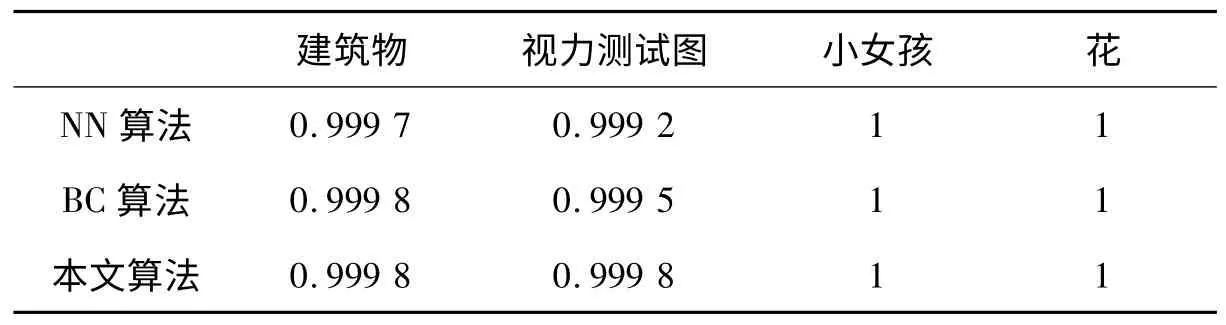
表2 实验结果比较(SSIM 指标)

图2 4 幅低分辨率测试图像
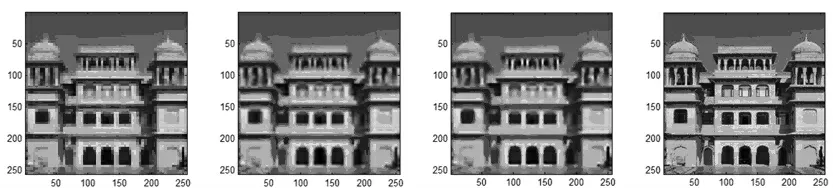
图3 从左到右依次为NN 算法、BC 算法、本文算法建筑物的超分辨率的效果与原图像
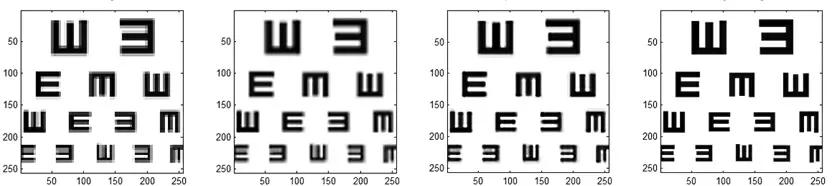
图4 从左到右依次为NN 算法、BC 算法、本文算法视力测试图的超分辨率的效果与原图像
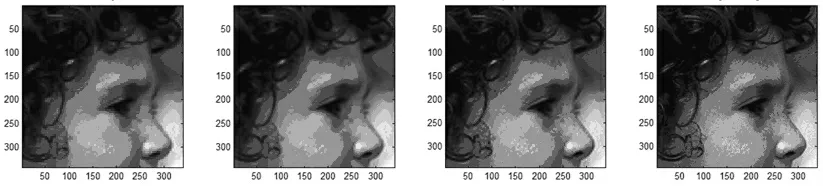
图5 从左到右依次为NN 算法、BC 算法、本文算法小女孩的超分辨率的效果与原图像

图6 从左到右依次为NN 算法、BC 算法、本文算法花的超分辨率的效果与原图像
5 结语
本文提出的算法在保证超分辨率图像质量的前提下,克服了对样本库的依赖性.实验证明了本文算法的优越性.下一步的工作是进一步考虑在学习字典时如何提取更有效的特征,如何节省更多的计算时间.
[1]Yang Jianchao,Wright J,Huang T S,et al.Image super-resolution as sparse representation of raw image patches[C]//CVPR.Anchorage:IEEE,2008:1-8.
[2]Goto T,Suzuki S,Hirano S,et al.Fast and high quality learning based super-resolution utilizing TV regularization method[C]//ICIP.Brussels:IEEE,2011:1185-1188.
[3]Tang Yi,Pan Xiaoli,Yuan Yuan,et al.Local semi-supervised regression for single-image super-resolution[C]//MMSP.Hangzhou:IEEE,2011:1-5.
[4]Yang Shuyuan,Wang Min,Chen Yiguang,et al.Single-image super-resolution reconstruction via learned geometric dictionaries and clustered sparse coding[J].ICIP,2012,21(9):4016-4028.
[5]Jiang Junjun,Hu Ruimin,Han Zhen,et al.Efficient single image super-resolution via graph embedding[C]//ICME.Melbourne:IEEE,2012:610-615.
[6]Glasner D,Bagon S,Irani M.Super-resolution from a single image[C]//Computer Vision.Kyoto:IEEE,2009:349-356.
[7]Chen Shaofeng,Gong Hanjie,Li Cuihua.Super resolution from a single image based on self-similarity[C]//ICCIS.Chengdu:IEEE,2011:91-94.
[8]He Kaiming,Sun Jian,Tang Xiaoou.Guided image filtering[M].Berlin:Springer-Verlag,2010:1-14.
[9]Yang Jianchao,Wang Zhaowen,Lin Zhe,et al.Coupled dictionary training for image super-resolution[J].ICIP,2012,21(8):3467-3478.
[10]Wang Zhou,Bovik A C,Sheikh H R,et al.Image quality assessment:From error visibility to structural similarity[J].ICIP,2004,13(4):600-612.
[11]Zhou Fei,Yang Wenming,Liao Qingming.Single image super-resolution using incoherent sub-dictionaries learning[J].IEEE Transactions on Consumer Electronics,2012,58(3):891-897.

