圆柱超声换能器的负载特性及其电声效率＊

刘世清，朱天宇，王娉婷，董 飞，杨先莉

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

0 引言

径向复合圆柱压电超声换能器辐射面积大，声辐射效率较高，在超声清洗、降解及声化学反应等液体超声处理技术领域获得广泛应用［1-4］.目前，在功率超声技术领域，换能器的共振频率方程通常是在假定无负载的情况下得出的，原因是换能器实际工作时的负载情况相当复杂，如在超声振动切削、焊接及超声钻孔等超声加工领域，随着工具头的不断磨损，换能器的负载阻抗是时变的，负载阻抗的变化势必影响换能器的输出特性及效率.由于负载阻抗变化的复杂性，且难以确定，因此，目前对有负载换能器的振动特性研究较少［5-6］.

换能器通常工作在有负载的情况下，负载阻抗不同，换能器的输入阻抗及谐振频率会随之发生改变.因此，研究有载换能器的振动特性更具有工程实际意义.径向复合圆柱压电超声换能器主要应用于液体超声处理领域，其在液体介质中的负载特性相对容易确定.

本文以前期研究工作中的径向复合压电超声换能器为研究对象，对其在液体介质中的负载特性进行了研究，探讨了其在液体介质中的声辐射阻抗及其共振频率随负载的变化规律，并对其在液体负载下的电声效率进行了初步的实验研究.

1 液体介质中的声辐射阻抗

如图1 所示，设圆柱超声换能器置于柱形容器中央.换能器沿径向辐射柱面声波，其辐射声压是轴对称的，声压p 仅是坐标r 及时间t 的函数，其在柱坐标系中的波动方程为

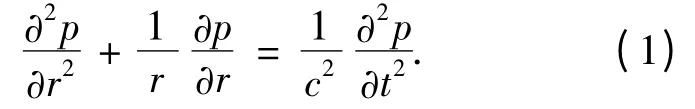
方程式(1)的通解可表示为

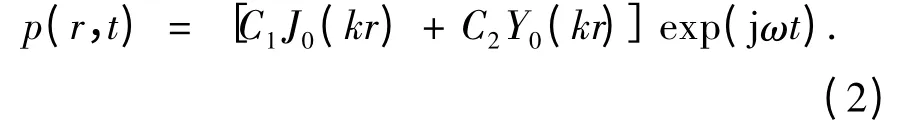
图1 柱形容器内液体介质中声辐射示意图

式(2)中:C1，C2分别为待定系数，由边界条件确定;J0(kr)，Y0(kr)分别为零阶一类和二类贝塞尔函数;k=ω/c 为波数;c 为介质中的声速.质点径向振速为

式(3)中:ρ 为液体密度;J1(kr)，Y1(kr)分别为一阶一类和二类贝塞尔函数.利用式(2)、式(3)得换能器在液体中的径向辐射声波阻抗为

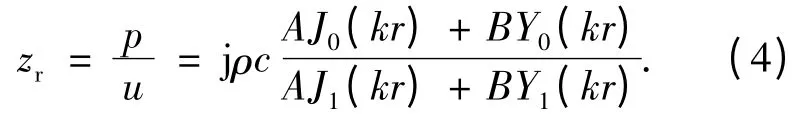
容器通常为金属材料，声波在液体与容器壁界面产生反射形成驻波声场.将容器壁近似地看作刚性边界，则分界面处始终为振速波节.设柱形容器的半径为R0，边界条件可写为

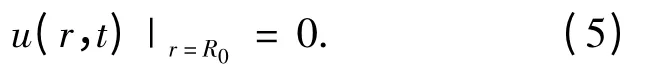
由式(3)、式(5)可得待定常数之比为

将式(6)代入式(4)，可得波阻抗表达式为

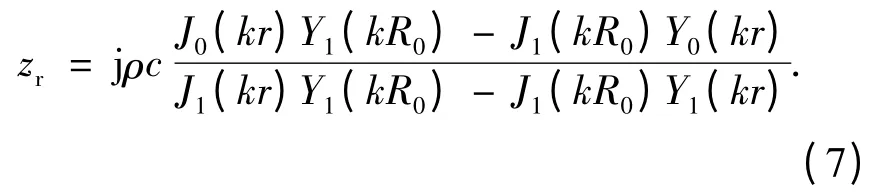
若圆柱换能器的半径为a，长为l，则可得到换能器辐射面处的声辐射阻抗为

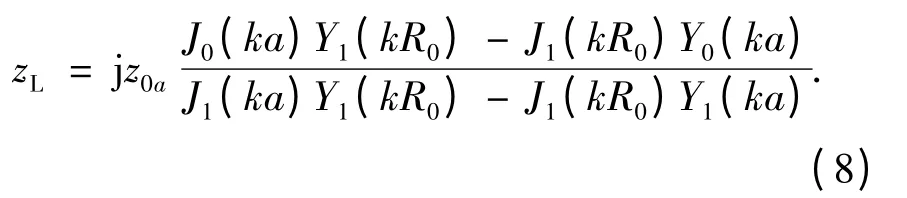
式(8)中，z0a=2palρc.以水介质为算例，并取参数ρ=1 000 kg/m3;c=1 480 m/s;a=30 mm;l=40 mm，计算得辐射阻抗zL随半径R0(或液面半径)的变化关系如图2 所示.

图2 负载阻抗与容器半径的关系

从图2 可以看出，辐射阻抗随容器半径在－∞～∞周期性变化.阻抗为零相当于“短路”;阻抗为无穷大相当于“开路”，后者将导致换能器制动而停止声辐射.这是在工程设计中必须注意的问题.

2 有载圆柱超声换能器的频率方程

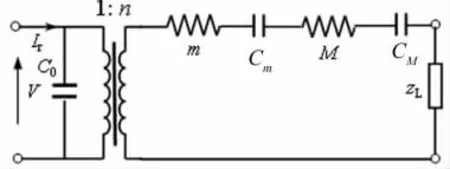
图3 有负载圆柱压电超声换能器等效电路

由图3 得，有负载时换能器的电输入阻抗为

式(9)中:

由式(9)可得，有负载的圆柱压电超声换能器的径向共振频率方程为

作为算例，利用频率方程式(12)计算了水介质中换能器的共振频率及阻抗特性，结果如图4所示.换能器参数如下.

2)预应力管:材料为硬铝，ρ=2 700 kg/m3;υ=0.34;E=71.5 GPa;内径52 mm;外径60 mm;长为40 mm;w=4 mm.

图4 是圆柱形容器直径为180 mm 时，圆柱换能器在水介质中的输入阻抗与频率之间理论关系.从图4 可以看出，当超声频率为20～40 kHz时，换能器的输入阻抗出现若干“零”点，每个零点对应一个谐振频率.但空载换能器在此频率范围内只有单一理论谐振频率(24.69 kHz).说明换能器在液体介质中辐射声波时会产生谐波.进一步分析表明，容器半径越大，谐波数量越多，且存在高于及低于换能器的空载谐振频率的谐波成分.这是由于液体中驻波声压起伏而导致换能器输入阻抗的周期性变化所引起的.

图4 圆柱换能器输入阻抗与频率的关系

3 实 验

3.1 液体负载下换能器的共振频率测定

首先，实验测定水负载下换能器的谐波共振频率，为此，研制了圆柱压电超声换能器如图5 所示.该换能器由2 节PZT4 压电陶瓷管沿轴向并通过热胀冷缩法嵌入预应力管中.压电陶瓷管几何尺寸为前述理论计算中给出.外部铝制应力管外径为60 mm，声波辐射有效长度为80 mm.装配后换能器空载实测共振频率为24.13 kHz.柱形容器材料为不锈钢，直径180 mm，高度300 mm.实验原理如图6 所示.依据声波的界面反射理论，金属容器壁处为声压波幅.因此，水听器安装在靠近容器壁的位置.以水为负载，实验中保持换能器的输入电功率为50 W，并将水听器的输出声压信号输入计算机处理系统进行处理.在20～40 kHz时测得水负载下换能器的各谐波共振频率如表1所示.从表1 可以看出，理论值ft和实验测试结果fm吻合较好.误差主要来源:一方面由于容器壁较薄，不完全满足刚性界面反射条件;另一方面，空化效应也会引起一定的实验误差.此外，实验发现，各谐波共振频率的强度不同，靠近换能器主共振频率的谐波共振相对较强.

图5 径向复合圆柱超声换能器照片

图6 实验原理图

表1 液体负载下换能器的谐波频率

3.2 换能器电声效率测量

电声效率是功率超声换能器的重要性能指标之一.换能器辐射功率和效率的测量一般比较复杂，目前，大功率夹心式纵向振动压电换能器辐射功率和效率的测量方法主要有瓦特计法、功率特性曲线法等［7］.由于本文研究的径向振动圆柱超声换能器主要用于液体超声处理，其辐射声场分布具有柱对称性.因此，本文主要利用水听器对换能器在水介质中的辐射声压进行多点测量，并对换能器的电声效率进行初步计算.

实验原理如图6 所示.主要仪器:UGD 通用型功率超声电源(含阻抗匹配箱)，频率10～100 kHz 可调，最大输出功率500 W;CALTEK CA2171型声强测量仪(含水听器，带宽1～100 kHz);DF3390B 数字频率计;不锈钢容器.

测量在水介质中进行.

测量方法:多点平均法.

测试参量:远场测试某处驻波波腹的声压(仪器以电压显示).驻波场中，声强测量仪测得的电压有效值与声强的关系为

式(3)中，u 为测得的电压有效值.

实验中保持超声电源输入电压U=150 V 不变，此时电流为I=1.12 A.

3.2.1 径向辐射声场分布测试

将水听器探头位置与换能器中心置于液体中同一深度处，在距换能器轴线135 mm 的圆周上测得各点电压(声压)数据拟合曲线如图7.由图7可见，圆柱换能器的径向辐射柱对称性较好.

图7 周向声场分布

3.2.2 纵向声场分布

将水听器探头始终置于某一驻波波腹位置(实验中为距换能器中心半径100 mm 处)，此处声辐射强度最大，然后从换能器有效辐射区上端开始，逐渐改变水听器探头的深度位置d，测得相应的纵向电压数据u 如表2 所示.电压随深度d的变化曲线如图8 所示.

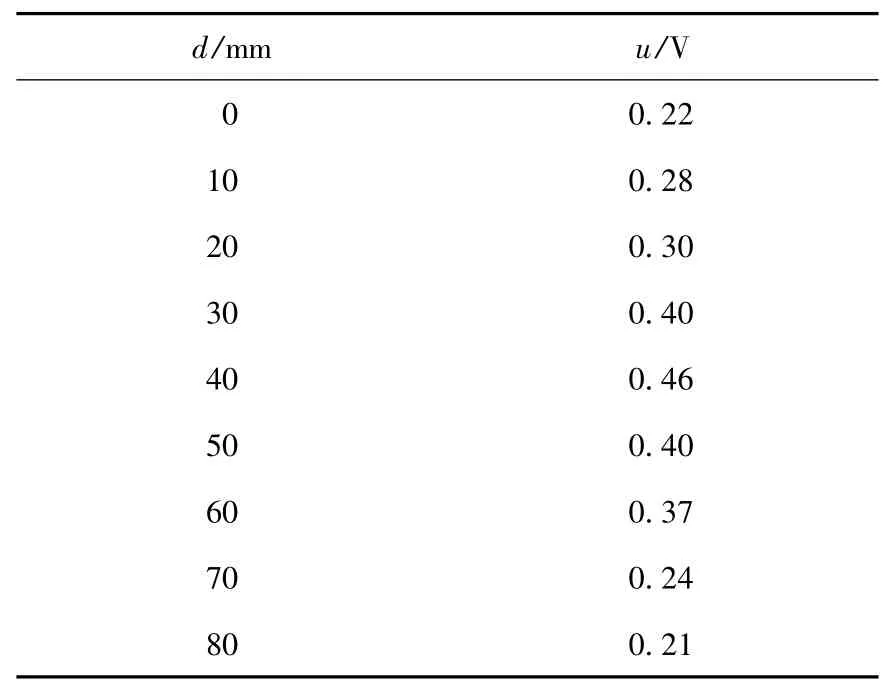
表2 不同深度处电压测量值

图8 电压随深度的分布

由图8 可以看出，声压沿纵向分布是不均匀的，圆柱换能器中部区域声辐射较强，两端辐射较弱.这与圆柱换能器的有限元模态仿真结果一致.

换能器径向辐射均匀，但在高度方向上不均匀.为此，在高度方向相邻2 点取平均值，分别求得平均电压u.一般实验采用的声强测量仪，其声强与电压关系Ia=4u2，是针对无界空间行波场标定的，而本实验测量在容器中进行，为有界驻波场.根据驻波场与行波场能量密度的关系［8］，可得声强与电压关系由式(13)给出.因此，换能器的径向辐射平均声功率为

计算得圆柱换能器在水介质中辐射时的电声效率为69.6%.

由于未加预应力，水声领域常用的圆柱压电换能器电声效率一般为40%左右.上述结果表明，带预应力管的圆柱压电换能器电声效率较高.

4 结论

1)推导出了复合管压电超声换能器在液体介质中的柱面波辐射阻抗表达式，并给出了辐射阻抗随液面半径的变化关系.计算表明，辐射阻抗随液面半径在－∞～∞作周期性变化.

2)得出了有载径向复合圆柱压电超声换能器的等效电路及径向共振频率方程.计算了在水介质中，换能器的阻抗频率特性及其共振频率随液面半径变化的理论关系.结果表明，因辐射阻抗的周期性变化，换能器在液体中会产生谐波共振.

3)通过实验测量了换能器在液体中的谐波频率，理论与实验结果符合较好.同时对换能器在液体中的电声效率进行了测量.结果表明，通过对压电陶瓷管施加预应力能较大幅度提高换能器的电声效率，以满足功率超声的应用要求.

应指出，本文对圆柱压电换能器电声效率的实验测量是粗略的.事实上，换能器电声效率的精确测量是功率超声的一个难点问题，有待进一步研究.

［1］Lin Shuyu.The radial composite piezoelectric ceramic transducer［J］.Sensors and Actuators A:Physical，2008，141(1):136-143.

［2］Liang Zhaofeng，Zhou Guangping，Zheng Yihui，et al.Vibration analysis and sound field characteristics of a tubular ultrasonic radiator［J］.Ultrasonic，2006，45(1/2/3/4):146-151.

［3］Gachagan A，Speirs D，McNab A.The design of a high power ultrasonic test cell using finite element modeling techniques［J］.Ultrasonic，2003，41(4):283-288.

［4］刘世清，姚晔.管形径向复合压电陶瓷超声换能器［J］.上海交通大学学报:自然科学版，2011，45(2):252-256.

［5］Banno H，Masamura Y，Naruse N.Acoustic load dependency of electro-acoustic efficiency in the electro-strictive ultrasonic transducer and acoustical matching［J］.Ultrasonic，1979(3):63-66.

［6］林书玉.夹心式功率超声压电换能器的负载特性研究［J］.陕西师范大学学报:自然科学版，2002，30(2):29-33.

［7］王爱玲，祝锡晶，吴秀玲.功率超声振动系统［M］.北京:国防工业出版社，2006.

［8］罗万前.驻波的能量分布［J］.四川师院学报:自然科学版，1981，9(2):47-54.