极限海况下Spar 平台系泊系统耦合动力分析
单鹏昊,任慧龙,李 辉,张 健
(哈尔滨工程大学 船舶与海洋工程力学研究所,黑龙江 哈尔滨 150001)
Spar 平台是在柱形浮标和张力腿平台概念的基础上提出的一种用于深水的生产平台,适合于500 至3 000 m 水深。经过30 多年的发展,技术不断创新,凭借良好的灵活性、优异的经济性和优良的动力稳定性等特点,成为海洋石油深水开发中极具竞争力的新一代平台。
为了研究整个Spar 平台系泊系统的耦合动力响应特性,学者们采用各种方式进行了计算分析。AGARWAL A K 和JAIN A K[1]研究了规则波作用下Spar 平台的非线性耦合动力响应特性;Xiaohong Chen、Jun Zhang[2]等采用准静态方法和动力耦合方法,并借以模型试验对Spar 系泊系统进行了计算分析;Spanos P D[3]等应用Monte Carlo 和统计线性化方法进行了耦合分析;TAHAR A 和KIM M H[4]考虑系泊缆索的材料特性,研究了聚酯纤维材料的系泊缆索和Spar 平台的耦合作用;高喜峰等[5]对Spar 平台系泊系统中立管的影响进行了计算,孙金伟等[6]对系泊方式对耦合动力响应的影响进行了分析,王兴刚等[7]考虑了不同参数对Spar 平台系泊系统的影响;刘利琴[8]研究了Spar 平台的垂荡-纵摇不稳定性;李彬彬等[9]对一种深吃水多立柱平台进行了耦合分析;张帆等[10]对一种新型立柱式平台做了实验研究。
对于不具有定位能力的Spar 平台而言,在复杂的海洋环境中,利用系泊系统进行定位是一种经济有效的方式。然而在遭遇极限海况时,平台的安全性很大程度上依赖于其系泊系统,极有可能发生一根或者多根缆索断裂的事故。当缆索断裂后,平台运动和系泊缆索张力的动力响应特性是工程上最为关注的。
1 数值方法
1.1 Classic-Spar 平台时域耦合运动方程
首先应用基于势流理论的边界元方法,考虑平台螺旋侧板对垂荡水动力特性的影响[11],在频域内计算波浪作用下平台的水动力响应,然后将频域水动力结果转换到时域,得出平台在不规则波浪和风流联合作用下的时域运动方程:
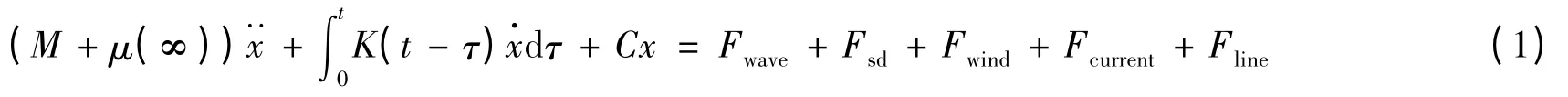
式中:M 为平台的广义质量矩阵,μ(∞)为附加质量矩阵,K(t)为平台运动的延迟函数矩阵,C 为恢复力矩阵,Fwave、Fwind、Fcurrent、Fline和Fsd分别为一阶波浪激励力、脉动风力、定常流力、系泊缆索力、不规则波有义波高和谱峰频率对应规则波的二阶平均波浪力,x 为Classic-Spar 的六自由度位移。
1.2 系泊缆索对Spar 平台的耦合作用
系泊缆索在外界激励的扰动下将产生显著的几何构型变化,同时由于其内部存在较高的张力水平,弹性变形不可忽略,杆中的拉伸应力相对于弯曲应力占主导地位,因此忽略弯曲刚度。
系泊缆索在顶部扰动、自身重量、流体外力的作用下产生运动,其动力控制方程[14]表示如下:

T'为张力对弧长的导数,W-B 为缆索净重力,F 为流体载荷,I 为惯性力。
基于完全拉格朗日格式,运用两节点等参缆索单元的几何非线性有限元方法可以解决系泊缆索的动力问题。
考虑缆索在固定的笛卡尔坐标系,在某种外力下连续的改变其位形,如图示。0xi(i =1,2,3)表示缆索处于0 时刻位形内任一点P 的坐标,用0xi+d0xi表示和点P 临近的Q 点在0 时刻的位形内的坐标。由于外力的作用,在以后的某个时刻,缆索运动并变形到新的位形,用txi和txi+d'xi表示点P 和点Q 在t 时刻位形内的坐标。
采用虚位移原理推导缆索的动力控制方程:

图1 坐标系内缆索的运动和变形Fig.1 Movement and deformation of a mooring line
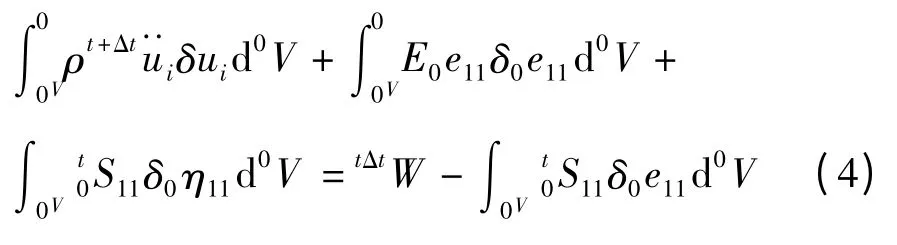
式中:
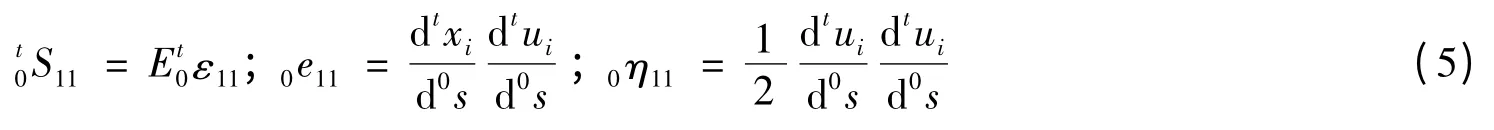
用等参缆索单元的插值函数表达离散缆索坐标和位移分量,将表达后的各分量带入式(15)得到完全拉格朗日(T·L·)格式求解缆索动力分析的方程[15]:

其中各个物理量均以0 时刻位型为参考,且为待求时刻的值,其中t+Δt为加速度列向量,t+Δtu 为位移列向量,M 为质量矩阵为附加质量矩阵为线性刚度矩阵为非线性刚度矩阵为节点载荷向量为单元应力的节点力向量。最后应用mN-R 迭代方法和Newmark 方法求解系泊缆索的动力响应状态。
在耦合模型的建立过程中,Spar 平台被视为一个位于重心处的节点,导缆孔被模拟为另一单独的节点,通过这两个节点的位置关系将平台的运动特性和系泊系统的运动特性结合起来。这样,在耦合计算时,系泊缆索的动张力是平台的外加输入载荷,平台运动是缆索上端的边界条件。由于在每个时间步里平台运动方程和系泊缆索运动方程都是同时求解的,这样就可以得到在每个时刻平台运动与缆索张力的变化特性。
1.3 近场积分法计算二阶力平均波浪力
文中采用可以给出二阶力全部六个分量的近场法计算。如果除去二阶速度势及二阶运动相关的项,并着重考虑一阶项之间的耦合,则二阶平均漂移力和力矩的表达式分别如下:
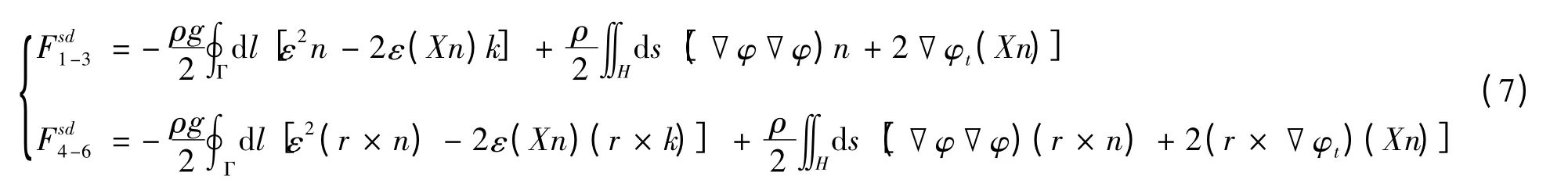
上述二阶平均漂移力都是由一阶量贡献得到,ε 是一阶自由面升高,φ 是一阶速度势,X =T +(R ×r)=(X1,X2,X3)为任意点处的位移,T=(x1,x2,x3)和R=(x4,x5,x6)分别是参考点处的平动和转动位移,r =(x -x0,y-y0,z-z0)为任意点相对于参考点处的位置向量。Γ 为平台处于平衡位置时的湿表面H 与平均自由面(z=0)的交线;法向量n 指向流体域内部。
2 Classic-Spar 平台系泊系统和环境参数
Spar 平台与系泊缆索的参数见表1 和表2。建立平台与系泊系统在极限风浪流作用下的耦合计算模型,见图2 和图3。极限海况下平台的环境参数如下:波浪谱选用JONSWAP 谱,有义波高为11.9 m,谱峰周期为12.2 s,谱峰参数取2.0,风谱选用DAVENPORT 谱,参考高度是水面以上10 m 处,平均风速取42.9 m/s,流为均匀流,流速为1.0 m/s。

表1 Spar 平台主尺度参数

表2 Spar 平台系泊缆索参数
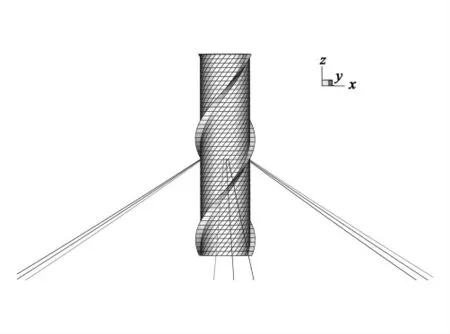
图2 Spar 平台湿表面网格划分Fig. 2 The wetted surface of the Spar platform
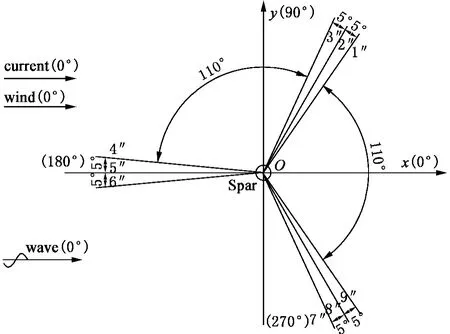
图3 Spar 系泊系统平面布置Fig.3 Sketch of the mooring system
3 计算结果分析
基于上述理论方法,平台一阶频域水动力结果由哈尔滨工程大学的WALCS 软件计算得到,编写后续的FORTRAN 程序,对极限海况下的Spar 平台系泊系统作了耦合动力分析。模拟时间3 个小时,运动方程计算的时间步长取Δt=0.05 s,每根系泊缆索划分50 个单元。
3.1 系泊缆索未断时平台运动响应谱和张力谱特性
在极限海况中风浪流的联合作用下,系泊缆索未断时,图4 为平台纵荡时程,图5 为缆索张力最大值所在的第5 根的张力时程,图6、图7、图8 分别是平台的纵荡、垂荡和纵摇谱。图9、图10 分别是每组系泊缆索中间根(2 号、5 号和8 号)的张力谱。
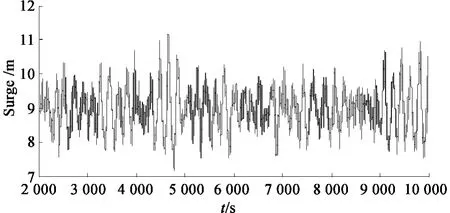
图4 缆索未断时平台纵荡时程Fig.4 Spar surge time series without broken lines

图5 缆索未断时5 号缆索张力时程Fig. 5 Line 5 tension time series without broken lines
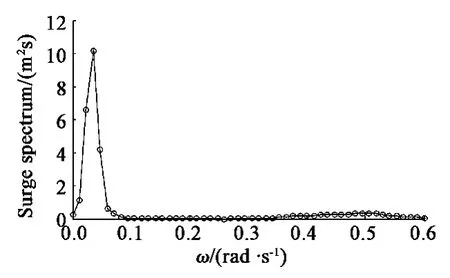
图6 缆索未断时平台纵荡谱Fig.6 Spar surge spectrum without broken lines
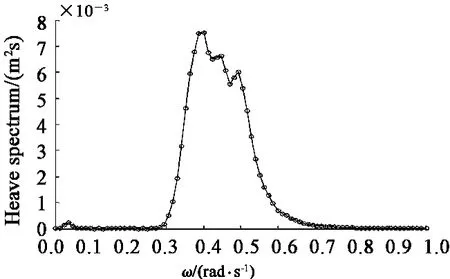
图7 缆索未断时平台垂荡谱Fig.7 Spar heave spectrum without broken lines

图8 缆索未断时平台纵摇谱Fig.8 Spar pitch spectrum without broken lines
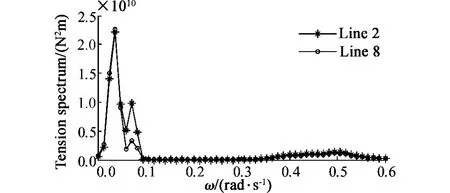
图9 缆索未断时2、8 号张力谱Fig.9 Line 2 and line 8 tension spectrum without broken lines
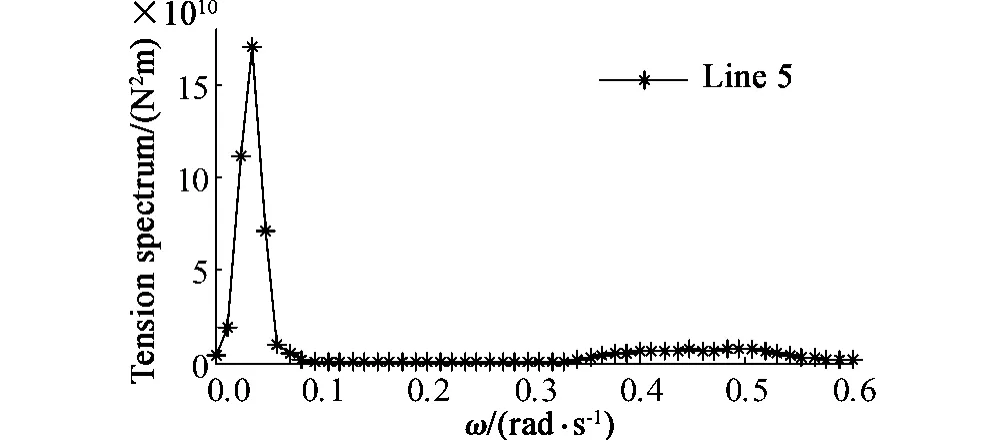
图10 缆索未断时5 号张力谱Fig.10 Line 5 tension spectrum without broken lines
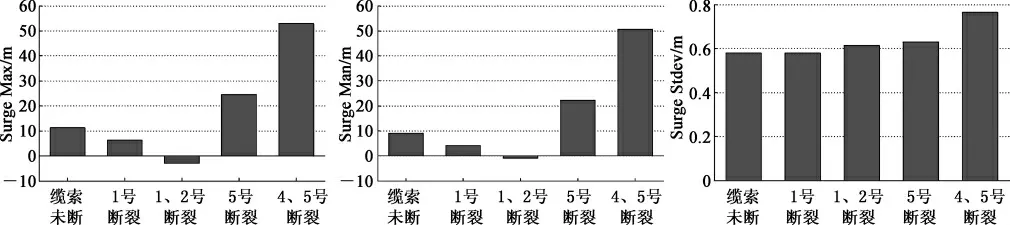
图11 不同位置缆索断裂时平台纵荡运动的最大值、平均值和标准差Fig. 11 The max,mean and stdev of Spar surge with different broken lines

图12 不同位置缆索断裂时平台垂荡运动的最大值、平均值和标准差Fig.12 The max,mean and stdev of Spar heave with different broken lines
分析图10 ~图12 可以发现:在极限风浪流联合作用下,平台纵荡和纵摇运动表现出明显的低频运动特性,而纵荡运动在ω=0.5 rad/s 的波频范围内会出现相对较小的响应峰值;平台的垂荡运动则表现出明显的波频特性,在ω=0.5 rad/s 的波频附近出现响应峰值。
该海况风浪流同向且共线,根据系泊缆索的布置特点可以得知缆索第2 根和第8 根应具有一致的张力响应特性,由图13 可以看出2 号和8 号具有大致相同的张力响应谱特性,张力谱都表现出明显的低频特性,只是在波频ω=0.5 rad/s 处有较小的峰值出现。而在迎浪侧的5 号缆索也有大致相同的谱峰分布特性,但是在峰值的大小上,5 号缆索要高出7 倍左右。经计算比较迎浪侧缆索较其他要大,其中5 号缆索张力峰值最大,而背浪侧的两组缆索相对较小。
3.2 缆索断裂时平台运动和缆索张力分析
在极限海况下,可能发生某根缆索断裂的事故,这时平台系统的动力响应是工程应用中尤其应该关注的问题。下面分别针对平台不同位置处系泊缆索有一根或多根发生断裂时平台三自由度运动和此时最大值缆索张力所在缆索的最大值、平均值、标准差等统计值的变化情况。根据上述缆索未断时的张力计算结果,这里重点考虑背浪侧缆索1 号断裂和1、2 号同时断裂,迎浪侧5 号断裂和4、5 号同时断裂,对4 种情况下的平台运动响应及系泊张力的变化作了分析。
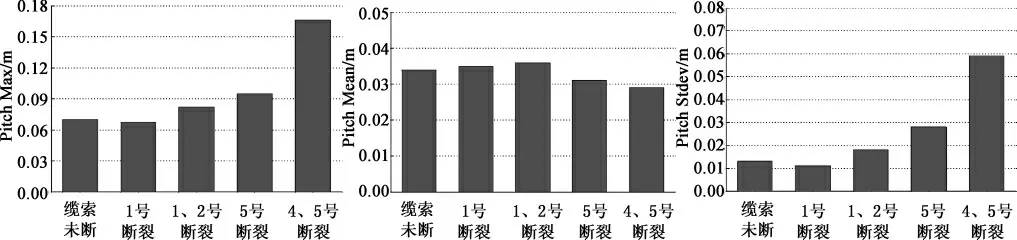
图13 不同位置缆索断裂时平台纵摇运动的最大值、平均值和标准差Fig. 13 The max,mean and stdev of Spar pitch with different broken lines
分析图11、图12、图13 和图14 可以发现:背浪侧1 号缆索断裂和1、2 号断裂两种情况会减小平台的纵荡位移的最大值和均值,对标准差的影响不大,这是因为当缆索断裂情况下,会改变平台在预张力作用下的平衡状态,平台纵荡运动会向断裂缆索的对侧偏移,恰好此时平台遭遇环境载荷的方向与上述偏移相反,进而导致了纵荡位移的减小;可以看出,当1、2 号同时断裂时,在当前的预张力水平和海况的影响下,平台纵荡位移出现了反向;此时对垂荡和纵摇运动的统计值影响相对比较小,最大缆索张力所在缆索的张力的最大值、均值和标准差都有不同程度的减小,且在此时,整个系泊系统的张力最大值只有预张力的水平。
当迎浪侧的5 号缆索断裂和4、5 号同时断裂时,与前述分析类似,但是结果完全相反,平台的纵荡位移有急剧增大的趋势,且当4、5 号同时断裂时,纵荡位移最大值达到52.9 m,是未断裂时11.61 m 的4.6 倍;平台垂荡和纵摇位移也有相应的偏移出现,而且对纵摇位移标准差的影响趋势要比其他两自由度剧烈;由于水平面内的纵荡位移对系泊缆索的张力的影响是最为直接的,图14 可以看出,5 号缆索断裂时,最大张力所在的4 号缆索的最大值和均值都有明显的影响,当4、5 号同时断裂时,此时系泊系统的张力最大值是未断裂时的2 倍左右。从平台的安全角度考虑,迎浪侧缆索的断裂对平台的安全影响较背浪侧大。
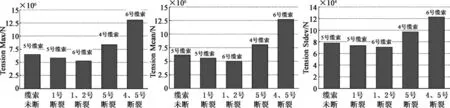
图14 不同位置缆索断裂时最大缆索张力所在缆索的最大值、平均值和标准差Fig. 14 The max,mean and stdev of the line which has the max tension with different broken lines
4 结 语
在极限海况下,考虑风浪流的联合作用,采用非线性时域耦合分析方法,分析Classic-Spar 平台及其系泊缆索的动力响应特性。通过分析Spar 系泊系统在所有系泊缆索未断裂时的平台运动和缆索张力特性,确定重点分析缆索断裂的几种情况。数值分析结果表明,几种缆索断裂情况对Spar 平台运动(尤其是水平面内的纵荡运动)和缆索张力动力响应特性都有明显的影响,但是从平台的安全角度考虑,在当前的预张力水平和海况下,迎浪侧缆索的断裂对平台影响最大。在工程实践中,针对多种海况,结合相关模型试验,并采用时域耦合的研究方法对平台系统有缆索断裂时的动力响应特性进行分析,是更具有工程应用意义的。
[1]AGARWAL A K,JAIN A K.Nonlinear coupled dynamic response of offshore Spar platforms under regular sea waves[J].Ocean Engineering,2003,30(4):517-551.
[2]CHEN X,ZHANG J,MA W.On dynamic coupling effects between a spar and its mooring lines[J].Ocean Engineering,2001,28(7):863-887.
[3]SPANOS P D.Coupled analysis of a spar structure:Monte Carlo and statistical linearization solutions[J].Journal of Offshore Mechanics And Arctic Engineering-transactions of the ASME,2005,127(1):11-16.
[4]TAHAR A,KIM M H.Coupled-dynamic analysis of floating structures with polyester mooring lines[J].Ocean Engineering.2008,35(17-18):1676-1685.
[5]高喜峰,张则青,阴宾宾.深海Spar 平台系泊系统耦合动力分析[J].海洋技术,2010,29:70-73.
[6]孙金伟,王树青.系泊模式对Spar 平台运动性能的影响[J].中国海洋大学学报:自然科学版,2010,49:147-153.
[7]王兴刚,孙昭晨,梁书秀. 深水Spar 平台在不规则波中的运动响应[J],中国造船,2011(2):16-24.
[8]刘利琴,唐友刚,王文杰.Spar 平台垂荡-纵摇耦合运动的不稳定性[J].船舶力学,2009(04):551-556.
[9]李彬彬,欧进萍. 深吃水多立柱平台的运动响应分析[J].中国造船,2010,51(2):107-116.
[10]张 帆,杨建民,李润培. 一种新型Spar 平台概念的试验研究[J].中国造船,2005,46(B11):293-298.
[11]王兴刚,孙昭晨,梁书秀,等. 水深和螺旋侧板对Classic-Spar 水动力特性的影响[J].中国海洋平台,2011(1):23-30.
[12]俞聿修. 随机波浪及其工程应用[M].大连:大连理工大学出版社,2000.
[13]Yusong Cao . A procedure for evaluation,assessmemnt and improvement of added mass and radiation damping of floating structures[C]∥OMAE.2008:163-172.
[14]缪国平. 挠性部件力学导论[M]. 上海:上海交通大学出版社,1996.
[15]王勖成. 有限单元法[M]. 北京:清华大学出版社,2003.

