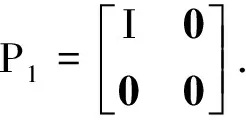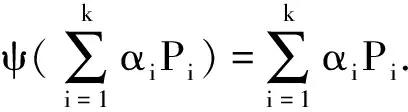自伴算子代数上保投影映射

张芳娟

(1.西安邮电大学理学院，中国 西安 710121；2.西安外事学院工学院，中国 西安 710077)

保持问题的一个重要内容是寻找一些代数或几何不变量作为算子代数的同构不变量.即，以尽可能少的代数或几何性质刻画算子代数间的同构问题.这个问题的研究最初是在线性的前提下[1-2].最近一些学者将线性条件减弱为可加或非线性[3-10].令B(H)是无限维Hilbert空间H上的所有有界线性算子全体，Dolinar[4]得到了B(H)满射满足A-λB是幂等算子当且仅当φ(A)-λφ(B)是幂等算子,或者存在有界可逆线性算子或有界可逆共轭线性酉算子T：H→H,使得对任意A∈B(H),有φ(A)=TAT-1,或者存在有界可逆线性算子或有界可逆共轭线性酉算子T：H→H，使得对任意A∈B(H),有φ(A)=TA*T-1.

设H是维数大于2的复Hilbert空间，B(H)是H上的所有有界线性算子全体；S(H)是H上的所有自伴算子全体；P(H)是B(H)中的正交投影的集合，即P(H)={P∈B(H):P=P2=P*}.设φ:S(H)→S(H)是满射，如果对λ∈C,A,B∈B(H),有A-λB∈P(H)⟺φ(A)-λφ(B)∈P(H)成立,则称φ双边保投影.取P，Q∈P(H),若PQ=QP=0，则称P与Q是正交投影；取A，B∈B(H),若AB=BA=A，则称A≤B.

S(H)是复Hilbert空间H上的自伴算子全体组成的集合.则S(H)是实线性空间.众所周知，在量子力学的框架下，Hilbert空间上的有界自伴算子即为有界可观测量.因此S(H)上的各种保持问题吸引了许多学者的关注.受文献[4]的启发，本文刻画了自伴算子空间上保投影映射.

本文的主要结论如下：

定理1设H是维数大于2的复Hilbert空间，P(H)={P∈B(H):P=P2=P*}.S(H)是H上的自伴算子代数.φ:S(H)→S(H)是满射,且对λ∈C,A,B∈B(H),满足A-λB∈P(H)⟺φ(A)-λφ(B)∈P(H)当且仅当存在酉算子或共轭酉算子U：H→H,使得对任意A∈S(H),有φ(A)=UAU*.

证充分性显然成立,分下面5步证明必要性.

1)φ(0)=0,φ(I)=I且φ是单射.

由0-λ·0=0∈P(H),λ∈C，得φ(0)-λφ(0)=(1-λ)φ(0)∈P(H).由λ的任意性得φ(0)=0.

设φ(A)=I,则A∈P(H).又φ(I)<φ(A)=I,因此φ(A)-φ(I)∈P(H)⟺A-I∈P(H).所以A=I，于是φ(I)=I.若φ(A)=φ(B),A,B∈S(H),则φ(A)-φ(B)∈P(H)⟺A-B∈P(H).又φ(B)-φ(A)∈P(H)⟺B-A∈P(H).于是A=B，因此φ是单射.

2) 对所有A∈S(H)，λ∈C,有φ(λA)=λφ(A).

当λ=0时，由于φ(0)=0,则φ(λA)=λφ(A)成立.当λ∈C{0}时，对所有A∈S(H),λA-λA∈P(H)⟺φ(λA)-λφ(A)∈P(H).令Q=φ(λA)-λφ(A).又A-(1/λ)(λA)∈P(H)⟺φ(A)-(1/λ)φ(λA)∈P(H),则-(1/λ)Q=φ(A)-(1/λ)φ(λA)∈P(H).由λ的任意性得Q=0，即φ(λA)-λφ(A)=0.

3)φ双边保投影的正交性.

若P，Q是相互正交的非零投影，则φ(P),φ(Q),P+Q∈P(H),P+Q∈P(H)⟺φ(P)+φ(Q)∈P(H).进而由(φ(P)+φ(Q))2=φ(P)+φ(Q)得

φ(P)φ(Q)+φ(Q)φ(P)=0.

(1)

(1)式分别左乘和右乘φ(P)得φ(P)φ(Q)=φ(Q)φ(P)=0.

同理可得φ-1保正交投影，所以φ双边保投影的正交性.

4)φ双边保一秩投影.

设P为一秩投影，若rankφ(P)≥2,则对任意一秩投影Q，有0

同理可得φ-1保一秩投影，所以φ双边保一秩投影.

5) 存在酉算子或共轭算子U：H→H使得对任意A∈S(H)有φ(A)=UAU*.

由于φ|P(H)是作用在P(H)上的双边保正交的双射，由文献[11]或[12]可得存在一个酉算子或共轭酉算子U：H→H使得对任意P∈P(H)有φ(P)=UPU*.

令ψ(A)=U*φ(A)U,则ψ(P)=P.下面用数学归纳法证明ψ在S(H)上都是恒等算子，即对任意A∈S(H)有ψ(A)=A.

当m=1时，由2)，对α1∈R,P1∈P(H),有ψ(α1P1)=α1ψ(P1)=α1P1.

(2)

则C∈P(H)..

(3)

进而

P1-αkD+αkPk∈P(H).

(4)

由(2)得

(5)

由(3)得

(6)

由(5)和(6)可知

αkPk-αkD=P1-C.

(7)

由(4)和(7)，P1-αkD+αkPk=2P1-C∈P(H).于是(2P1-C)2=4P1-2P1C-2CP1+C=2P1-C，即

P1+C=P1C+CP1.

(8)

(9)

若α1≠0,则由2)和(9)式得

因此ψ在S(H)上是恒等算子，即对任意A∈S(H)有ψ(A)=A.则存在酉算子或共轭酉算子U：H→H使得对任意A∈S(H)有φ(A)=UAU*.

参考文献：

[2] LI C K, TSING N K. Linear preserver problems:a breif introduction and some special techniques[J]. Linear Algebra Appl, 1992,162-164(1):217-235.

[3] DOLINAR G. Maps on matrix algebras preserving idempotents[J]. Linear Algebra Appl, 2003,371(1):287-300.

[4] DOLINAR G. Maps on B(H) preserving idempotents[J]. Linear and Multilinear Algebra, 2004,52(5):335-347.

[5] SONG X F, CAO C G. A note on k-potence preserving maps[J]. Linear Algebra Appl, 2008,429(7):1579-1586.

[6] LAJOS M. Two characters of additive-automorphism of B(H)[J]. Bull Aust Math Soc, 1996,53(2):391-400.

[7] 郭志林，陆风玲.一类非线性广义神经传播方程非协调元超收敛分析[J].湖南师范大学自然科学学报, 2011,34(6):1-5.

[8] 蒋明霞.带非线性扩散项的中立双曲方程的振动判据[J].湖南师范大学自然科学学报, 2011,34(6):12-15.

[10] ZHANG J, ZHANG F. Nonlinear maps preserving Lie products on factor von Neumann algebras[J]. Linear Algebra Appl, 2008,429(1):18-30.

[11] UHLHORN U. Reprsentation of symmetry transformations in quantum mechanics[J]. Ark Fysik, 1963,23(1):307-340.

[12] 白朝芳，侯晋川.保正交性与|·|k交换的可加映射[J].数学学报， 2002,45(5):863-870.

[13] PEARCY C, TOPPING D. Sums of small numbers of idempotents[J]. Mach Math J， 1967,14(1):453-465.