谱Legendre-Galerkin方法求解线性积分微分方程的超几何收敛性分析
李气发,谢资清,,陶 霞
(1.贵州师范大学数学与计算机科学学院,中国 贵阳 550001;2.湖南师范大学数学与计算机科学学院,中国 长沙 410081)
Volterra积分微分方程广泛应用于物理、生物、控制论等自然科学领域.该类方程中的积分项反映了实际过程中的记忆或反馈性质,使得它与传统的微分方程有着本质的区别.如何快速、高效而准确地求解这类问题是科学计算中的重要问题.
早期关于积分微分方程的数值方法主要是差分方法[1].近年来,Hesthven[2],Tang[3-4], Guo[5]和Wang[6]等在用谱方法求解积分微分方程方面做了大量的工作,使得这方面研究逐渐引起了学者们的关注.事实上,谱方法具有“无穷阶”的收敛性,即如果原方程解无限光滑,那么适当的谱方法求得的近似解将以N-1的任意幂次速度收敛于精确解.特别是谱方法适合于求解非常规则而几何区域维数非常大的问题.
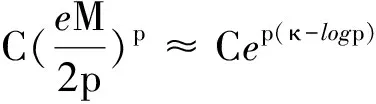
最近,Tang[14]等采用节点上的谱配点法求解带光滑核的第二类积分方程.在此基础上,Xie[15]等采用谱和伪谱Jacobi-Galerkin方法求解第二类Volterra积分方程,并进行了严格的收敛性分析.他们最近又进一步证明了M-条件,以及Galerkin谱方法求解上述积分方程的超几何收敛性.
本文采用谱Legendre-Gelerkin方法求解第二类Volterra积分微分方程,在一定的假设条件下,证明了解满足M-条件,并证明了谱Legendre-Galerkin方法在L2和L∞意义下的超几何收敛性质.事实上其结果相比文献[17]中的谱Petrov-Galerkin方法能够达到更高的收敛率.
首先考虑具有如下形式的一般线性Volterra积分微分方程(VIDEs):
(1)
y(0)=y0,
(2)
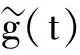
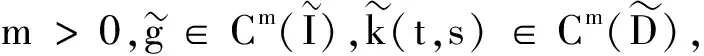
事实上,方程(2)等价于
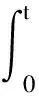
(2′)
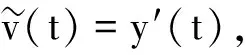
(3)
(4)
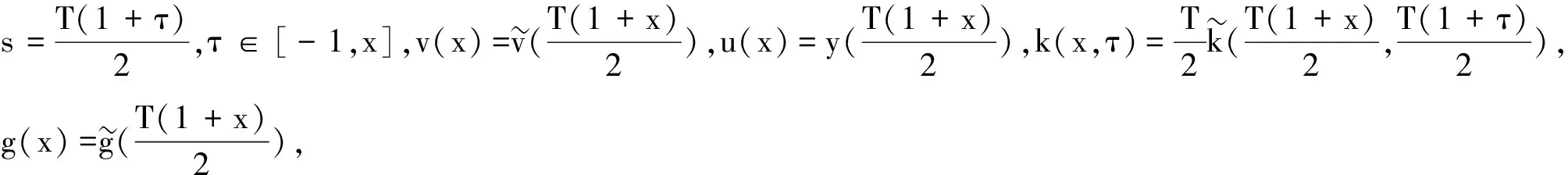
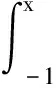
(5)
(6)
1 谱Legendre-Galerkin方法
(7)
首先讨论谱Legendre-Galerkin方法的数值实现.令PN是定义在[-1,1]上的次数不超过N的多项式构成的空间,Lj(x)是j次Legendre多项式,j=0,1,…,N.即有PN=span{L0(x),L1(x),…,LN(x)}.
谱Legendre-Galerkin方法为:对(7)式寻求uN∈PN,vN∈PN,使得
(vN,wN)-(uN,wN)-(SuN,wN)=(g,wN),∀wN∈PN,
(8)
(uN,wN)-(KvN,wN)=(u0,wN),∀wN∈PN,
(9)
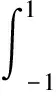
(10)
将式(10)分别代入(8)和(9),并取wN=Li(x),i=0,1,…,N,可得
(11)
(12)
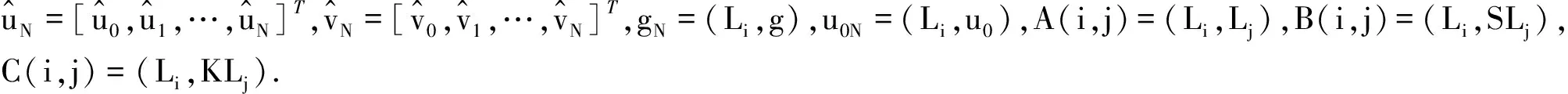
2 一些有用的引理
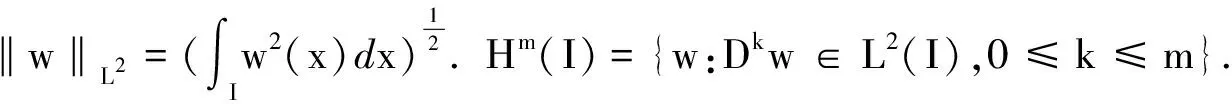
定义正交投影算子ΠN:L2(I)→PN,使得对任意的u∈L2(I)都有(ΠNu,wN)=(u,wN),∀wN∈PN.
最后,考虑方程(7),为使解满足M-条件,需要作以下假设:
令D={(x,τ):-1≤x≤1,-1≤τ≤x},I=[-1,1].
(A1)g(x)和k(x,τ)分别在I和D上充分光滑,且k(x,τ)=k(x-τ).
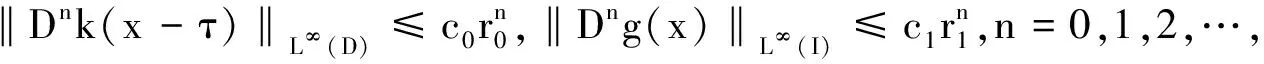
引理2(M-条件)如果条件(A1)和(A2)成立,则存在常数c和M≥max{r0,r1},使得方程(7)的解u和v满足‖u(n)(x)‖L∞(I)≤cMn,‖v(n)(x)‖L∞(I)≤cMn,n=0,1,2,….
证由文献[17]中定理3.1可直接得到.
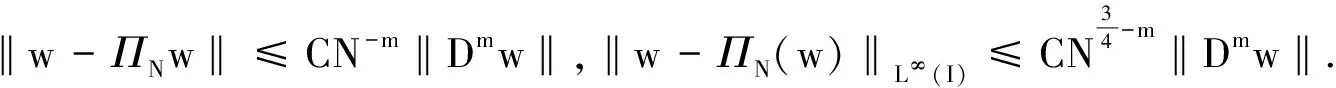
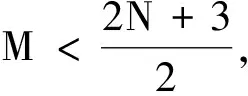
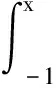
3 谱Legendre-Galerkin方法的超几何收敛性分析
根据式(8),(9)和投影算子ΠN的定义,(8),(9)等价于
vN-uN-ΠNSuN=ΠNg,
(13)
uN-ΠNKvN=u0.
(14)
定理1满足方程(8)和(9)的谱Legendre-Galerkin解存在且唯一.
证设uN,vN为(8)和(9)的谱Legendre-Galerkin解.由于解空间是有限维,且问题(8)和(9)与(13)和(14)等价,为此只要证明(13)和(14)中,当g=0,u0=0时,uN=0,vN=0即可.为此考虑
vN-uN-ΠNSuN=0,
(15)
uN-ΠNKvN=0.
(16)
将(16)代入(15)得
vN-ΠNKvN-ΠNSuN=vN-KvN+(KvN-ΠNKvN)-SuN+(SuN-ΠNSuN)=
vN-KvN+(KvN-ΠNKvN)-S[ΠNKvN]+(SuN-ΠNSuN)=0.
(17)
即有
vN=KvN+S[ΠNKvN]-(KvN-ΠNKvN)-(SuN-ΠNSuN).
(18)
对上式的第2项,根据k(x,τ)的光滑性,并运用Dirichlet公式
(19)
可得
|S[ΠNKvN]|=|S[KvN-(KvN-ΠNKvN)]|≤|S(KvN)|+|S(KvN-ΠNKvN)|≤
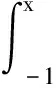
(20)
由(18),(20)可得
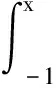
(21)
根据([6]p.239,Lemma 3.7)有
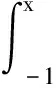
(22)
令H1=SuN-ΠNSuN,H2=KvN-ΠNKvN,由(21),(22)及引理4可得
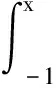
C(‖H1‖+‖H2‖).
(23)
根据引理3有
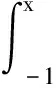
CN-1‖uN‖.
(24)
同理可得
‖H2‖≤CN-1‖vN‖.
(25)
由(23)~(25)可得,当N足够大时
‖vN‖≤CN-1‖uN‖.
(26)
由(16),(22)和(25)可得
‖uN‖≤‖KvN‖+‖KvN-ΠNKvN‖≤C‖vN‖+CN-1‖vN‖≤C‖vN‖.
(27)
从(26),(27)可以看到,当N充分大时,uN=0,vN=0.从而存在唯一性得证.
证分别将(7)中的第1,第2式与(13),(14)相减得
v-vN-(u-uN)-(Su-ΠNSuN)=g-ΠNg,
(28)
(u-uN)-(Kv-ΠNKvN)=0.
(29)
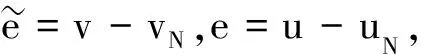
Su-ΠNSuN=Su-ΠNSu+ΠNS(u-uN)=Su-ΠNSu+S(u-uN)-{S(u-uN)-ΠNS(u-uN)}=
(-g+v-u)-ΠN(-g+v-u)+S(u-uN)-{S(u-uN)-ΠNS(u-uN)}=
-g+ΠNg+(v-ΠNv)-(u-ΠNu)+Se-(Se-ΠNSe).
(30)
同理可得
(31)
将(30),(31)分别代入(28),(29)得
(32)
(33)
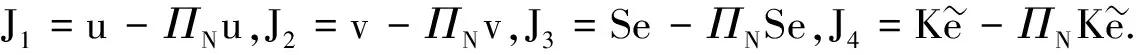
(34)
对(34)第2个等号右边第3项,运用公式(19)可得
(35)
由(34),(35)及k(x,τ)的光滑性可知,
(36)
由(36),(22)和引理4知,
‖J3‖+‖J4‖).
(37)
由假设(A1)和(A2),(7)的解满足M-条件.根据引理3,有
(38)
(39)
将(38),(39)代入(37)得到
(40)
由(33),(22)可得
(41)
另一方面,由(36)和引理4有
C(‖J1‖L∞‖+‖J2‖L∞+‖J3‖L∞‖+‖J4‖L∞‖).
(42)
再由引理3有
(43)
(44)
将(43),(44)代入(42)式并整理得
(45)
又由(33),(43)得
(46)
4 数值算例
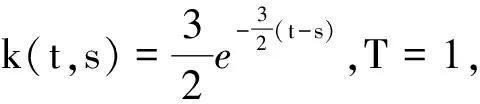
考察式(11),(12),采用谱Legendre-Galerkin方法求解算例.表1为谱Legendre-Galerkin方法近似解及近似导数解的L2和L∞误差,分别与图1(a)、(b)相对应.从误差数据和图中可以看出,该方法具有超几何收敛性.

表1 谱Legendre-Galerkin方法的误差
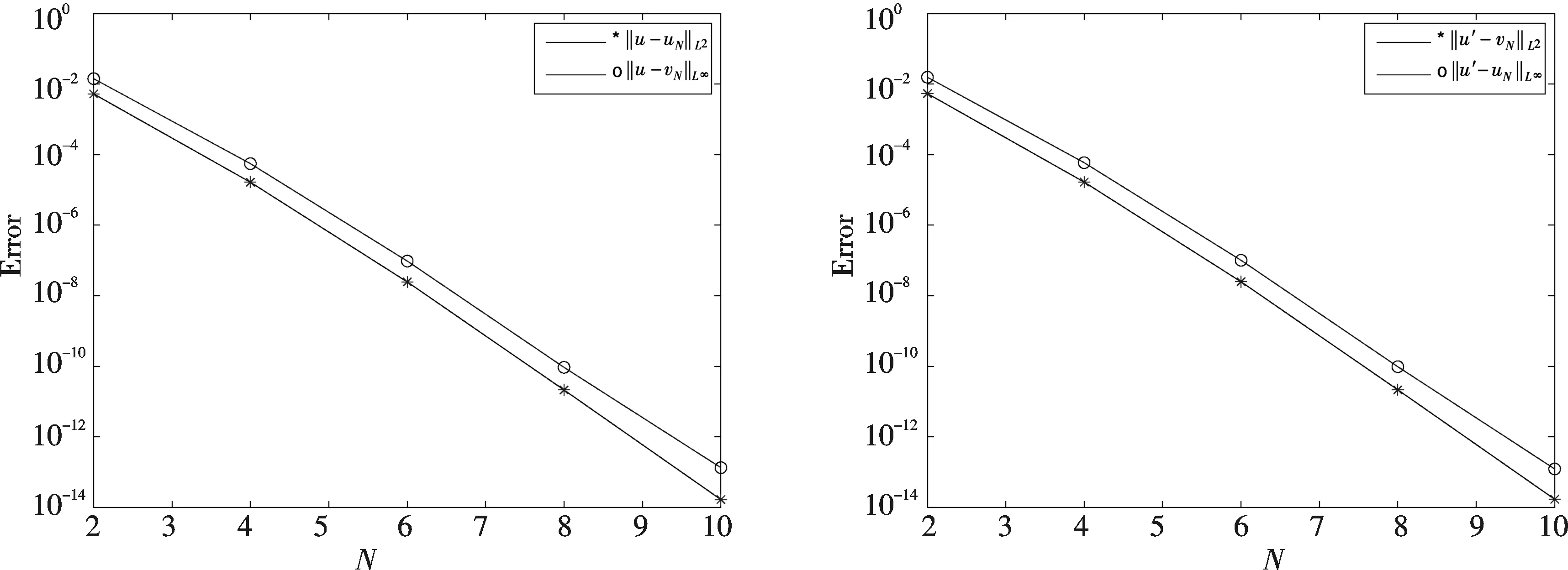
图1 (a)谱Legendre-Galerkin法近似解的误差 (b)谱Legendre-Galerkin法近似导数解的误差 Fig.1 (a) The error of approximate solution for the spectral (b) The error of approximate derivative solution for the spectral Legendre-Galerkin method Legendre-Galerkin method
参考文献:
[1] BRUNNER H. A survey of recent advances in the numerical treatment of Volterra integral and integral-differential equations[J]. J Comput Appl Math, 1982,8(3):76-102.
[2] HESTHVEN J S, GOTTLIED S, GOTTLIEB D. Spectral methods for time-dependent problems[M].New York:Cambridge University Press, 2007.
[3] SHEN J, TANG T. Spectral and high-order methods with applications[M].Beijing:Science Press, 2006.
[4] SHEN J, TANG T, WANG L L. Spectral method:algorithms, analysis and applications[M].New York:Springer, 2011.
[5] GUO B Y. Spectral methods and their applications[M].Singapore:World Scientific, 1998.
[6] GUO B Y, WANG L L. Jacobi interpolation approximations and their applications to singular differential equations[J].Adv Comput Math, 2001,14(3):227-276.
[7] BERNARDI C, MADAY Y. Handbook of Numerical Analysis:Spectral methods[J].Techniques of Scientific Computing(part 2), 1997, 5:209-485.
[8] GOTTLIEB D, ORSZAG T A. Numerical analysis of spectral methods:theory and applications[M].Philadelphia:SIAM, 1997.
[9] KARNIADAKIS G E, SHERWIN S J. Spectral/hp element methods for CFD[M].New York:Oxford University Press, 1999.
[10] TREFETHEN L N. Spectral methods in matlab[M].Philadelphia:SIAM, 2000.
[11] TAO X, XIE Z Q, ZHOU X J. Spectral petrov-Galerkin methods for the second kind volterra integro-differential equations[J].Numer Math Theor Meth Appl, 2011,4(2):216-236.
[12] WEI Y X, CHEN Y P. Legendre spectral collocation methods for pantograph Volterra delay-integro-differential equations[J].J Sci Comput, 2012,53(3):672-688.
[13] ZHANG Z. Superconvergence of spectral collocation andp-version methods in one dimensional problems[J].Math Comput, 2005,74(252):1621-1636.
[14] TANG T, XU X, CHEN J. On spectral methods for Volterra type integral equations and the convergence analysis[J].J Comput Math, 2008,26(6):825-837.
[15] XIE Z Q, LI X J, TANG T. Convergence analysis of spectral Galerkin methods for Volterra type integral equations[J].J Sci Comput, 2012,53(2):414-434.
[16] BRUNNER H. Collocation methods for Volterra integral and related functional equations[M].Cambridge:Cambridge University Press, 2004.
[17] 陶 霞.求解Volterra积分微分方程的高阶方法[D].长沙:湖南师范大学, 2012:33-36.

