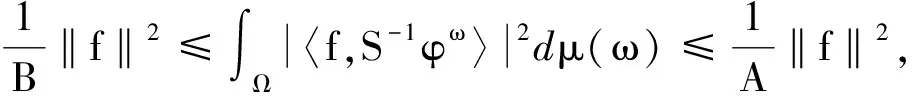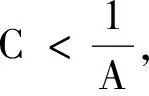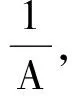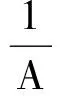连续框架的等价刻画及Riesz型框架的新结果
相中启,潘 伟
(华中师范大学数学与统计学院,中国 武汉 430079)
1952年,Duffin和Schaeffer在深入研究非调和Fourier级数时引入框架(离散框架)的概念[1].小波分析诞生以来,框架理论得到了迅速发展[2-3].它广泛应用于信号处理、图像处理和抽样理论等方面[4-7].连续框的概念由Kaiser[8],Ali等[9]分别独立引入,它是离散框架的概括,是一般化的框架.Gabardo和韩德广[10]称其为“与可测空间相关的框架”;Askari等[11]称其为“广义框架”;而在数学物理中则称其为“相干态”[9].目前,连续框架已广泛应用于连续小波变换及短时Fourier变换等方面[12-13].本文主要讨论了连续框架的等价刻画和连续框架的对偶问题.
全文组织如下:第1节列出本文所要用到的一些定义和基本事实并给出连续框架的2个等价刻画.第2节讨论了连续框架的对偶,给出了Riesz型框架的新结果.
1 连续框架的等价刻画
本文中,H,K始终指复的Hilbert空间,S指连续框架的框架算子.
定义1[10]设H是复的Hilbert空间,(Ω,μ)是赋有正测度μ的测度空间,{φω}ω∈Ω⊆H使得对所有的f∈H,

(1)
则称{φω}ω∈Ω关于(Ω,μ)是连续框架,A,B分别称为连续下、上框架界,所有上框架界的下确界称为最优上框架界,所有下框架界的上确界称为最优下框架界,显然最优框架界仍是框架界.若(1)式右端不等式成立,则称{φω}ω∈Ω是Bessel序列,B称为Bessel界.易见,若μ是计数测度,Ω:=,则{φω}ω∈Ω成为离散框架.此外,(1)式左端的不等式表明{φω}ω∈Ω是完备的,即
设{φω}ω∈Ω关于(Ω,μ)是H的界为A,B的连续框架,则
(2)
T*:H→L2(Ω,μ),(T*f)(ω)=〈f,φω〉,ω∈Ω.
(3)
由复合算子T和其共轭算子T*就得到框架算子
(4)
容易证明S有界,可逆且是自共轭的正算子.由此得到连续框架恢复公式
(5)
(6)
引理1[3]设W:K→H是有界线性算子,若其值域RW是闭的,则存在有界线性算子W†:H→K使得WW†f=f,∀f∈RW.算子W†称为W的伪逆算子.
进一步,Christensen证明了
引理2[3]设W:K→H是有界线性算子,若其值域RW是闭的,则
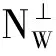
(ii) (W*)†W*是R(W*)†上的正交投影;
(iv) (W*)†=(W†)*.
下面的定理给出了连续框架的一个等价刻画.
定理1设{φω}ω∈Ω关于(Ω,μ)是H中的Bessel序列,则{φω}ω∈Ω关于(Ω,μ)是H的连续框架的充分必要条件是:(2)式所定义的算子T是满射.
证先证必要性.设{φω}ω∈Ω是H的界为A,B的连续框架,其预框架算子为T,由(2)式知
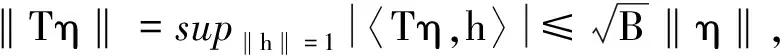
所以T*是单射,因此T是满射.
再证充分性.只需证明存在常数c1,c2(0 (7) 所以 接下来的定理同样给出了连续框架的等价刻画. 定理2{φω}ω∈Ω关于(Ω,μ)为H的界为A,B的连续框架当且仅当下面2个条件满足: (ii)预框架算子T是定义好的且 (8) 证首先假设{φω}ω∈Ω关于(Ω,μ)是H的界为A,B的连续框架,即 由Cauchy-Schwartz不等式得 因此‖Tη‖2≤B‖η‖2,于是(ii)成立. A‖T†Tη‖2≤‖TT†Tη‖2=‖Tη‖2. 即 这说明{φω}ω∈Ω满足下框架条件,上框架条件可以由(8)式右端的不等式直接得到. 定义2[10]设{φω}ω∈Ω,{ψω}ω∈Ω关于(Ω,μ)是H的连续框架,若对任意的f,g∈H 则称{ψω}ω∈Ω是{φω}ω∈Ω的对偶框架;若{φω}ω∈Ω的对偶框架唯一,则称{φω}ω∈Ω是Riesz型框架. 〈f,(TT*)-1f〉. 因此 综上可知{S-1φω}ω∈Ω是{φω}ω∈Ω的对偶框架. 下面的定理给出了预框架算子T的伪逆T†的详细刻画. 定理3设{φω}ω∈Ω关于(Ω,μ)是H的连续框架,T是其预框架算子,S是其框架算子,则 (T†f)(ω)=〈f,S-1φω〉,f∈H,ω∈Ω. 此外,若A,B是{φω}ω∈Ω的最优框架界,则A=‖S-1‖-1=‖T†‖-2,B=‖S‖=‖T‖2. 证由于{φω}ω∈Ω是H的连续框架,由定理1知T是满射,即RT=H.由引理1知,∀f∈H,TT†f=f.对任意的h∈H有 由(2)式知 因此 (T†f)(ω)=〈f,S-1φω〉,∀f∈H,ω∈Ω. 根据定义, 引理5[10]设{φω}ω∈Ω关于(Ω,μ)是H的连续框架,T是预框架算子.则{φω}ω∈Ω是Riesz型框架的充分必要条件是RT*=L2(Ω,μ). 下面给出Riesz型框架的新结果. 定理4{φω}ω∈Ω关于(Ω,μ)为H的界为A,B的Riesz型框架当且仅当下面2个条件满足: (ii)预框架算子T是定义好的且 A‖η‖2≤‖Tη‖2≤B‖η‖2,∀η∈L2(Ω,μ). (9) 推论1{φω}ω∈Ω关于(Ω,μ)为H的Riesz型框架的充分必要条件是(2)式所定义的算子T是定义好的双射. 参考文献: [1] DUFFIN R J, SCHAEFFER A C. A class of nonharmonic Fourier series [J]. Trans Amer Math Soc, 1952,72(2):341-366. [2] DAUBECHIES I. Ten lectures on wavelets [M]. Philadelphia: SIAM, 1992. [3] CHRISTENSEN O. An introduction to frames and Riesz bases [M]. Boston: Birkhäuser, 2002. [4] FEICHTINGER H G, STROHMER T. Gabor analysis and algorithms: theory and applications[M].Boston: Birkhäuser, 1998. [5] FEICHTINGER H G, STROHMER T. Advances in Gabor analysis [M]. Boston: Birkhäuser, 2003. [6] CASAZZA P G. Modern tools for Weyl-Heisenberg frame theory [J]. Adv Imag Elect Phys, 2001,115(1):1-127. [7] 王国秋,杨梦云.双正交小波的谱半径及其应用[J].湖南师范大学自然科学学报, 2011,34(1):14-18. [8] KAISER G. A friendly guide to wavelets [M]. Boston: Birkhäuser, 1994. [9] ALI S T, ANTOINE J P, GAZEAU J P. Continuous frames in hilbert spaces [J]. Ann Phys, 1993,222(1): 1-37. [10] GABARDO J P, HAN D. Frames associated with measurable space [J]. Adv Comp Math, 2003,18(3):127-147. [11] ASKARI-HEMMAT A, DEHGHAN M A, RADJABALIPOUR M. Generalized frames and their redundancy[J]. Proc Amer Math Soc, 2001,129(4):1143-1147. [12] ALI S T, ANTOINE J P, GAZEAU J P. Coherent states, wavelets and their generalizations [M].Berlin: Springer-Verlag, 2000. [13] GRÖCHENIG K. Foundations of time-frequency analysis [M]. Berlin: Birkhäuser-Verlag, 2001.

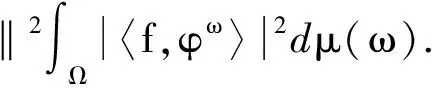


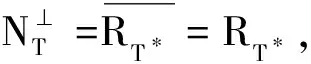


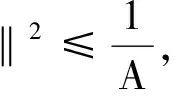
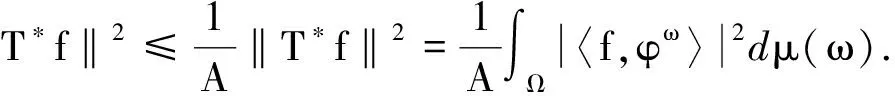

2 连续框架的对偶