基于可分辨矩阵的属性集依赖度计算方法

谢 科

(阿坝师范高等专科学校计算机科学系,中国 汶川 623002 )

粗糙集理论[1]于1982年由波兰学者Pawlak提出，现已被广泛应用于机器学习、数据挖掘等领域[2-6]，其核心研究内容就是依据决策表或者信息表的条件属性集、决策属性集以及对象集，进行知识约简从而获得最具代表性的属性约简集以及最简分类规则集[7-10]．知识约简包括属性约简和分类规则约简，目前国内外学者主要在属性约简方面进行研究[11]．

在属性约简中，衡量某个属性的重要程度一般是根据决策属性对该属性的依赖程度来做出判断，依赖度为1，则完全依赖；依赖度为0，则完全不依赖，其余则部分依赖[12]．对于那些依赖度为0的属性，一般认为并不影响决策表分类的结果，在属性约简时可以直接删除[13-14]．但是，这样不但会在某种程度上造成知识损失，而且还割断了该属性与其他属性的联系，从而造成更大程度的损失．

为此，本文在可分辨矩阵的基础上，研究属性集依赖度，提出了一种属性集依赖度计算方法，并用实例验证了该方法具有较好的有效性和较低的时间复杂度．

1 基本理论

设S=(U,A,V,f)是一个决策信息系统．其中：U是非空有限对象集，A=C∪D是属性集，C和D分别是条件属性集和决策属性，f:U×A→V是一个信息函数．

定义1[11]等价族.基于条件属性集B⊆C不可分辨关系的等价族表示为U|B=(X1,…,Xp)，其中Xj是由在属性集B上的属性值相等的对象xi构成的集合；基于决策属性D不可分辨关系的等价族表示为U|D=(Y1,…,Yq)，其中Yj(j=1,2,…,q)是由决策属性值相等的对象xi构成的集合．

定义2[11]正域.对于一个决策信息系统S=(U,A,V,f)，设根据条件属性B⊆C划分的等价族为Xi,i=1,2,…,p，根据决策属性D划分的决策属性等价族为Yj,j=1,2,…,q，则定义Yj的下近似集为：

P-(Yj)=∪{Xi∈U|Xi⊆Yj}，

(1)

其中i=1,2,…,p;j=1,2,…,q.

定义3[11]D的B正域表示为POSB(D)，即：

POSB(D)=∪P_(Yj),j=1,2,…,q.

(2)

系统的知识可以用决策属性D表达，也可以由条件属性C描述，这取决于数据库中函数之间的依赖性关系．

定义4[11]依赖度.设S=(U,A,V,f)是一个决策信息系统，A=C∪D是属性集，C和D分别是条件属性集和决策属性，基于条件属性集B⊆C描述决策属性D表达的知识，其可导性定义为知识的依赖性，表达为

(3)

称其为D以依赖度k(0≤k≤1)依赖于B，记作B⟹D，这里card()表示集合的基数．

定义5[11]可分辨矩阵.设S=(U,A,V,f)是一个决策信息系统，U={x1,x2,…,xn}为对象集,包含n条记录,A=C∪D是属性集，C={a1,a2,…,am}和D={d}分别是条件属性集和决策属性，包含m个条件属性和1个决策属性．对于任意2个对象xi和xj，定义可分辨矩阵的元素为

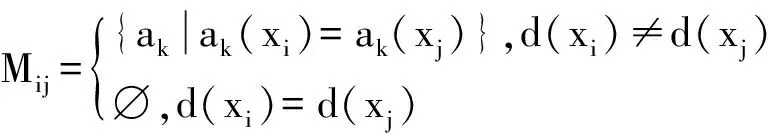
(4)

性质1当任一条件属性集B包含于分辨矩阵中的某个元素，即B⊆Mij，则决策表中的对象xi、xj∉POSB(D)．

证因为B⊆Mij，根据可分辨矩阵的定义，对象xi和xj的决策属性不同，即d(xi)≠d(xj)，但对于任意条件属性ak∈B，xi和xj的属性值相等，即ak(xi)=ak(xj)．根据正域的定义，即可得xi、xj∉POSB(D)．

定义6[11]属性集依赖度.设S=(U,A=C∪D,V,f)是一个决策信息系统，B⊂C为一个条件属性集(该属性集由1个以上的属性组成)，此时D对B的依赖度称为属性集依赖度．

2 本文所提属性集重要度评价方法

在一个决策信息系统中，如果存在多个条件属性的依赖度相等时，就无法判断哪个属性更重要．在这种情况下，就需要与其他条件属性(2个或2个以上)构成属性集并计算该属性集的依赖度，以此大小来分辨该属性的重要程度．文献[15]给出了一个属性集依赖度计算方法，具体算法描述如下：

Begin://划分等价类

for each 条件属性的组合

fori=1 ton

forj=i+1 ton

比较xi和xj的条件属性，属性值相同的归为一个等价类；

end

end

end

nCount=0；

for 每个等价簇

如果该簇中全部对象的决策属性值都相同,那么

nCount=nCount+该类对象数；

end for

return nCount/对象总数//返回属性依赖度

End

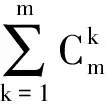
为克服上述算法的不足，本文在定义5的基础上，提出一个新的属性集依赖度计算方法，其描述如下：

Begin:

根据定义5求出分辨矩阵M；

A={x1,x2,…,xn}； //生成对象集

对于任意的属性集B

for eachA中的对象xi

if 分辨矩阵的第i行存在一个元素Mij，使得xk⊆Mij；

从A中删除xi和xj；

end if

end for

returnA中的对象个数/对象总数； //返回属性依赖度

End

如果有m个条件属性，n个对象，本文方法时间复杂度由以下2个部分组成：①分辨矩阵时间复杂度为O(m×n2)；②其余时间复杂度为O(m2×n)．则总的时间复杂度为O(m×n2+m2×n)，这同文献[15]方法的时间复杂度相比具有一定的优势．

3 实例验证

实验运行环境为2.00 GHz，1.99 GB RAM，Windows XP操作系统．为了全面地验证本文算法，选择如下6个实验数据集进行实验：①文献[15]中的1个决策信息表，具体如表1所示，共有8个对象，条件属性集C由属性{a,b,c,d}组成，决策属性为D．

表1 取自文献[15]的决策表

②California大学提供的UCI知识库中的Chess End-Game数据集，该数据集包括36个条件属性，1个决策属性，共3 196项记录．③California大学提供的UCI知识库中的Diabetes数据集，该数据包括8个条件属性，2个决策属性，共798项记录．

④California大学提供的UCI知识库中的Segmentation数据集，该数据集包括19个条件属性，7个决策属性，共2 932项记录．

⑤California大学提供的UCI知识库中的Breast数据集，该数据集包括9个条件属性，2个决策属性，共817项记录．

⑥California大学提供的UCI知识库中的Bupa数据集，该数据集包括6个条件属性，5个决策属性，共428项记录．

为了便于表达，本文算法简称NM，文献[15]算法简称OM，其实验结果如表2所示：

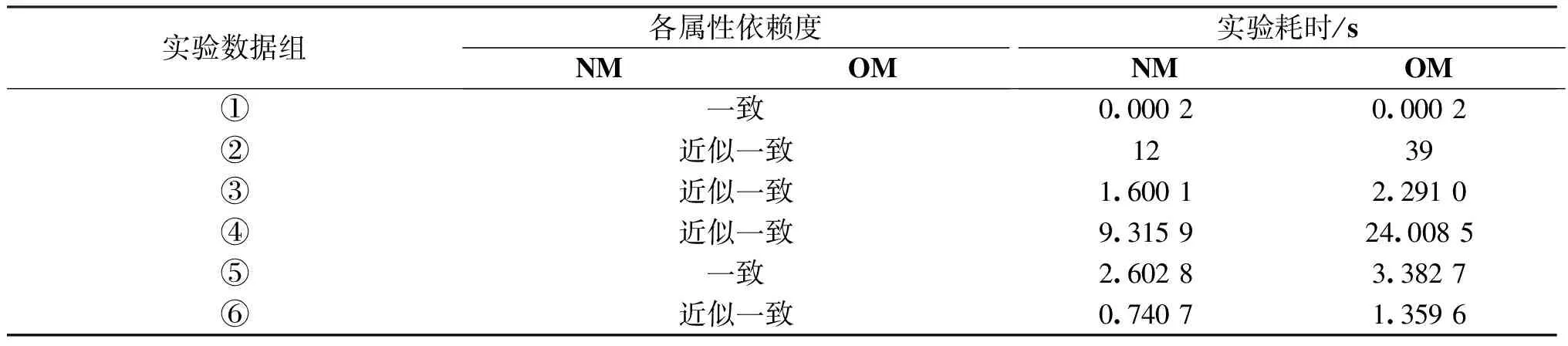
表2 NM和OM算法实验结果对比

从表2可以看出，对于本文算法和文献[15]算法，在各个实验数据集上，各属性依赖度的计算结果都近似一致，但本文算法的耗时较低，尤其是数据集较大的时候，这个优势更加明显．

4 结束语

在信息表中，那些依赖度等于0的属性也可能对其他属性产生影响.在这种情况下，属性集依赖度就更能反映现实情况．为此，本文提出了一个新型基于辨识矩阵的属性集重要度评价方法，实例验证了该方法的有效性和较低的时间复杂度，从而使得本文方法在属性约简中有一定的实用价值．

参考文献：

[1] 朱颢东,钟 勇.基于优化的文档频和粗糙集的特征选择方法[J].湖南师范大学自然科学学报, 2009,32(3):27-31.

[2] CHEN D G, HU Q H, YANG Y P. Parameterized attribute reduction with Gaussian kernel based fuzzy rough sets[J]. Int J Inform Sci, 2011,181(23):5169-5179.

[3] 黄媛玉,毛 弋.基于主成分分析法的遗传神经网络模型对电力系统的短期负荷预测[J].湖南师范大学自然科学学报, 2011,34(5):26-31.

[4] 胡 强.优化的互信息特征选择方法[J].湖南师范大学自然科学学报, 2010,33(3):28-31.

[5] KIYOSHI H, MICHAUD K, MASAMOTO A. Application of data mining to quantitative structure-activity relationship using rough set theory[J].Int J Chem Intell Lab Sys, 2009,99(1):66-70.

[6] MICHAEL N, GUDRUN S, GERHARD S. Adapted variable precision rough set approach for EEG analysis[J].Int J Artif Intell Med, 2009,47(3):239-261.

[7] 马建敏,张文修,朱朝晖. 基于信息量的序信息系统的属性约简[J]. 系统工程理论与实践, 2010,30(9)：1679-1683.

[8] FAN T F, LIAU C J, LIU D R. A relational perspective of attribute reduction in rough set-based data analysis[J].Eur J Opera Res, 2011,213(1):270-278.

[9] QIAN Y H, LIANG J Y, PEDRYCZ W. An efficient accelerator for attribute reduction from incomplete data in rough set framework[J].Pattern Recog, 2011,44(8):1658-1670.

[10] HE Q, WU C X, CHEN D G,etal. Fuzzy rough set based attribute reduction for information systems with fuzzy decisions[J]. Knowledge-Based Sys, 2011,24(5):689-696.

[11] 胡寿松,何亚群. 粗糙决策理论与应用[M]. 北京:北京航空航天大学出版社, 2006.

[12] YAO Y Q, MI J S, LI Z J. Attribute reduction based on generalized fuzzy evidence theory in fuzzy decision systems[J].Fuzzy Sets Sys, 2011,170(1):64-75.

[13] QIAN Y H, LIANG J Y, PEDRYCZ W. Positive approximation: an accelerator for attribute reduction in rough set theory[J].Artif Intell, 2010,174(9):597-618.