半导体中深能级的晶格弛豫效应
张 跃
(湖南师范大学物理与信息科学学院,中国 长沙 410081)
大量的实验结果表明,杂质缺陷在半导体的带隙中产生深能级,引起半导体材料的电学及光学等性质发生变化,因而是制作半导体器件需要考虑的重要因素之一.计算半导体中深能级的理论有待进一步完善,原因是有些理论计算结果与实验测量数据之间还存在较大的误差,这是因为在计算过程中忽略了某些应该考虑的影响,例如,杂质在半导体中引起的晶格弛豫效应.晶格弛豫效应引起的能级变化一般比较小,但是在处理一些半导体问题时,计及其影响,可以显著地改进理论计算结果与实验测量数据之间的偏差.关于考虑晶格弛豫效应对深能级影响的半导体缺陷问题,长期以来一直是半导体领域感兴趣的研究课题[1-6].
近似估算半导体深能级的晶格弛豫效应,可以在Hjalmarson等人提出的理论基础上[7],利用Harrison提出的与键长的平方成反比例的规则来进行[1,8].这种方法便于进行数值计算,但是只能够计算最近邻晶格弛豫效应.1984年,Baranowski提出了一个近似估算模型[9],可以计算包括替位杂质的最近邻以及次最近邻原子在内的晶格弛豫效应,从理论上作了更加完善的处理,适合于原子簇团的计算.本文将在有关研究的基础上,对于含各种杂质的几种常用半导体的晶格弛豫效应,进行一些数值计算和理论研究.
1 理论计算
1.1 Harrison 模型计算
考虑一个杂质原子替位于闪锌矿或者金刚石结构中的阴离子位置,由于杂质原子的能量与主体原子(不含杂质时,完整晶体的原子)的能量不相同,以及杂质原子的键长与主体原子的键长不相等,在晶体中产生一个缺陷势能,可以表示为[1]
(1)
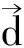
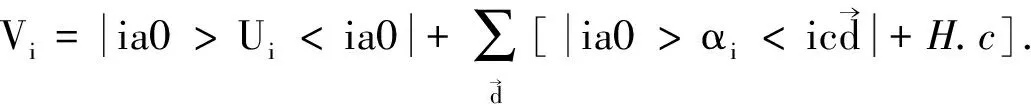
(2)
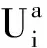
(3)
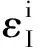
根据Harrison模型,由替位杂质原子在晶体中引起的最近邻晶格弛豫效应与原子的键长的平方成反比例,即:
(4)
式中的dI和dH分别表示杂质原子和最近邻主体原子的键长;Ci为比例常数,Ci前面取负号仅仅是为了计算方便.根据实验测量和经验分析,Ci(i=s,p)的数值分别取:CS=10.5 eVÅ2和CP=-3 eVÅ2[1].
采用(4)式计算晶格弛豫效应,我们规定:当dI>dH时,称为偏外弛豫,根据(4)式可以判断出相应的αS为正值,αP为负值;当dI dI=rI+rH, (5) 式中rI和rH分别表示杂质原子和最近邻主体原子的共价半径. 对于含各种杂质的Si,Ge和GaP,本文利用(4)式分别计算了它们的最近邻晶格弛豫效应(见表1). 从表1中的数据可以归纳出以下两点: (1) Harrison模型所考虑的最近邻晶格弛豫效应,是由于杂质原子的大小与最近邻主体原子的大小不同,因而杂质原子的键长与最近邻主体原子的键长不同,引起含杂质半导体体系中原子的键长发生变化所致. (2) 从本文计算得到的数据可以发现,对于所有杂质原子的键长大于最近邻主体原子的键长的半导体,它的A1对称态的最近邻晶格弛豫是偏外弛豫(αS>0),而它的T2对称态的最近邻晶格弛豫效应则必定是偏内弛豫(αP<0);对于所有杂质原子的键长小于最近邻主体原子的键长的半导体,它的A1对称态的最近邻晶格弛豫是偏内弛豫(αS<0),而它的T2对称态的最近邻晶格弛豫效应则必定是偏外弛豫(αP>0). 此外,从表1中可以发现,Pauling公式,即(5)式不适用于GaP:O(dI>dH),文献[12]中对此作了修正说明. 表1 含各种替位杂质的GaP,Si和Ge的共价半径,杂质原子的键长,最近邻主体原子的键长,以及根据Harrison模型计算得到的最近邻晶格弛豫效应的数值(本文计算) 注:a见参考文献[8];b见参考文献[10];c见参考文献[12]中未考虑修正的杂质的键长;d见参考文献[12]中经过修正之后的杂质的键长. 对于一些要求高精确度的半导体计算问题,计算晶格弛豫效应需要考虑包含大数量原子的原子簇团.这一点是Harrison模型所不能够做到的.Baranowski在1984年提出的近似估算公式,把计算晶格弛豫效应扩展到考虑次最近邻的主体原子.在Baranowski模型中,以Δd作为变量,Δd表示杂质原子与最近邻主体原子之间的键长的变化.我们规定:当Δd>0时,为偏外弛豫;当Δd<0时,为偏内弛豫. 晶格弛豫效应引起的系统的总能量的变化可以表示为 (6) (7) (8) 在应用Baranowski模型进行计算时,遇到一个困难问题,因为Δd和Δd′都可以大于或者小于零,会出现最近邻主体原子的键长和次最近邻主体原子的键长同时变长或者同时变短,这是违背实验结论的.为了避免这一点,可以将(7),(8)两式修正为 (9) 以及 (10) (11) 由(6),(9)和(10)式得到一个方程: (12) 主体-杂质系统k εh/eVb,ck′ ε′h/eVa,b,cV3/eVbV′3 /eVcΔd/nmΔd′/nmGaP:N(d0=0.235 8 nm)19.97 12.54 2.00 -0.041 5 0.013 8GaP:C 16.00 12.54 2.00 -0.024 30.008 1GaP:Sb 9.94 12.54 2.00 0.021 7-0.007 23GaP:O(d0>dI) 26.30 12.54 2.00 -0.065 1 0.021 7GaP:O(d0 注:a见参考文献[8];b见参考文献[2];c见参考文献[9]. 关于表2中的计算结果,作以下几点解释: (3) 表2中的Δd的数值显然不等同于表1中dH-dI的数值,这是因为相对于Harrison模型,Baranowski的理论考虑了更多影响最近邻主体原子键长变化的因素. 本文利用表2中的数据,代入(9)式和(10)式,对于最近邻晶格弛豫效应为偏内弛豫的几种含各种杂质的半导体,计算出了它们的最近邻和次最近邻晶格弛豫效应分别引起的总能量的变化.计算结果列于表3. 表3 含各种杂质GaP, Si和Ge的以及的数值计算结果(本文计算) 关于表3中的计算结果,作以下几点解释: (1) 对于含各种杂质的GaP,本文仅计算了次最近邻晶格弛豫效应引起的能量变化,这是因为作者暂时没有查找到相应于各种杂质的参数V3的实验测量数据. (2) 与表1中的数据相比较,可以发现,表3中的最近邻晶格弛豫效应引起的能量变化的数值与表1中的数值有微小的差别,原因是,对于Baranowski模型,引起键长变化的主要原因是平均杂化,而不是因为杂质原子和主体原子的大小不同. (3) 对于Si:Te和Ge:Te,晶格弛豫效应引起的能量变化都非常小,在半导体问题中可以忽略不计. 对于含杂质半导体,如果要求严格计算晶格弛豫效应产生的能级偏移,应该考虑对系统的总能量进行计算.晶格弛豫效应引起系统的总能量变化,使半导体的深能级向导带或者价带移动.但是,计算晶格弛豫效应与计算系统的总能量必须在理论上自洽.对于含各种杂质的Si,Ge和GaP的总能量,表4中列出了几种不同的计算结果,以及实验测量数据. 表4 含各种杂质的GaP, Si和Ge半导体的深能级 注:a见参考文献[13]和[14];b见参考文献[2];c见参考文献[7];d见参考文献[1]. 从表4中列出的数据可以发现: (1) 与Hjalmarson等人的计算结果相比较,计及Harrison的最近邻晶格弛豫效应,得到A1态的深能级的数值显然更加接近实验测量值.计及Baranowski的最近邻和次最近邻晶格弛豫效应,得到的A1态的深能级的值与实验测量数据也比较接近,但仍然存在一定的偏差,其原因目前尚未确定.表4中的实验数据全部是1982年以前测量获得的[2].所以,一方面,我们可以进一步改进对晶格弛豫效应的近似估算模型以及计算总能量的理论;另一方面,还可以与以后发表的实验测量数据进行比较. (2) 对于Si和Ge两种半导体材料,Te杂质引起的晶格弛豫效应对A1态的深能级影响非常小.尤其是,对比Hjalmarson等人的计算结果和计及Baranowski最近邻和次最近邻晶格弛豫效应的计算结果,并没有发现含Te杂质的Si的晶格弛豫效应对深能级产生任何影响,这一点与表3中的结果完全一致.而Te也是一种超导元素,因此,作者推测Te杂质在某些应用领域具有特殊的意义. 本文利用Harrison提出的与原子键长的平方成反比例的规则以及Baranowski的近似估算模型,对含各种杂质原子的几种常用半导体Si,Ge和GaP的晶格弛豫效应作了深入的研究,作了大量具有应用价值的计算工作(见表1~4).对于Baranowski模型,考虑到如果最近邻晶格弛豫效应偏外(Δd>0),则次最近邻晶格弛豫效应必然偏内(Δd′<0);反之亦然.本文对Baranowski的公式作了修正.表4中的计算结果表明,计及围绕杂质原子的最近邻和次最近邻的偏外或者偏内晶格弛豫,得到的数值结果更加接近实验测量数据. 但从表4中发现,利用几种理论计算的深能级的数值结果,尤其是计及Baranowski的最近邻和次最近邻晶格弛豫效应的深能级与实验测量值之间仍然存在一定的偏差,导致产生偏差的原因可能由于:电荷态分裂[15],应用于计算中的能带结构不精确,共价半径模型中出现断裂,也可能是其他目前尚不清楚的原因所致. 参考文献: [1] LI W G, MYLES C W. Effects of lattice relaxation on deep levels in semiconductors [J]. Phys Rev B, 1991,43(3):2192-2200. [2] TALWAR D N, SUH K S, TING C S. Deep levels due to chalcogen defects in Si-Ge solid solutions[J]. Phil Mag B, 1986,54(2):93-111. [3] RINKE P, JANOTTI A, SCHEFFLER M,etal. Defect formation energies without the band-gap problem: combining density-functional theory and the GW approach for the silicon self-interstitial[J]. Phys Rev Lett, 2009,102(2):206402. [4] LEE S, HWANG G S. Theoretical determination of stable fourfold coordinated vacancy clusters in silicon[J]. Phys Rev B, 2008,78(12):125310. [5] CARVALHO A, COUTINHO J, JONES R,etal. First-principles study of Fe and FeAl defects in SiGe alloys[J]. Phys Rev B, 2008,78(12):125208. [6] BUTORAC B, MAINWOOD A. Symmetry of the phosphorus donor in diamond from first principles[J]. Phys Rev B, 2008,78(23):235204. [7] HJALMARSON H P, VOGL P, WOLFORD D J,etal.. Theory of substitutional deep traps in covalent semiconductors[J]. Phys Rev Lett, 1980,44(12):810-813. [8] HARRISON W A. Electronic structures and the properties of solids[M]. San Francisco: Freeman, 1980. [9] BARANOWSKI J M. Bond lengths, force constants and local impurity distortions in semiconductors[J]. J Phys C, 1984,17(35):6287-6300. [10] KITTEL C. Introduction to solid state physics[M].6th ed. New York: Wiley,1986. [11] PAULING L. The nature of the chemical bond[M]. Ithaoa: Cornell University Press, 1967. [12] MORGAN T N. Electronic states of oxygen in gallium phosphide, an example of weak bonding[J]. Phys Rev Lett, 1982,49(2):173-176. [13] MILNES A G. Deep impurities in semiconductors[M]. New York: Wiley, 1973. [14] PANTELIDES S T. Deep centers in semiconductors[M]. New York: Gordon and Breach, 1973. [15] LEE S, DOW J D, SANKEY O F. Theory of charge-state splitting of deep levels[J]. Phys Rev B, 1985,31(6):3910-3914.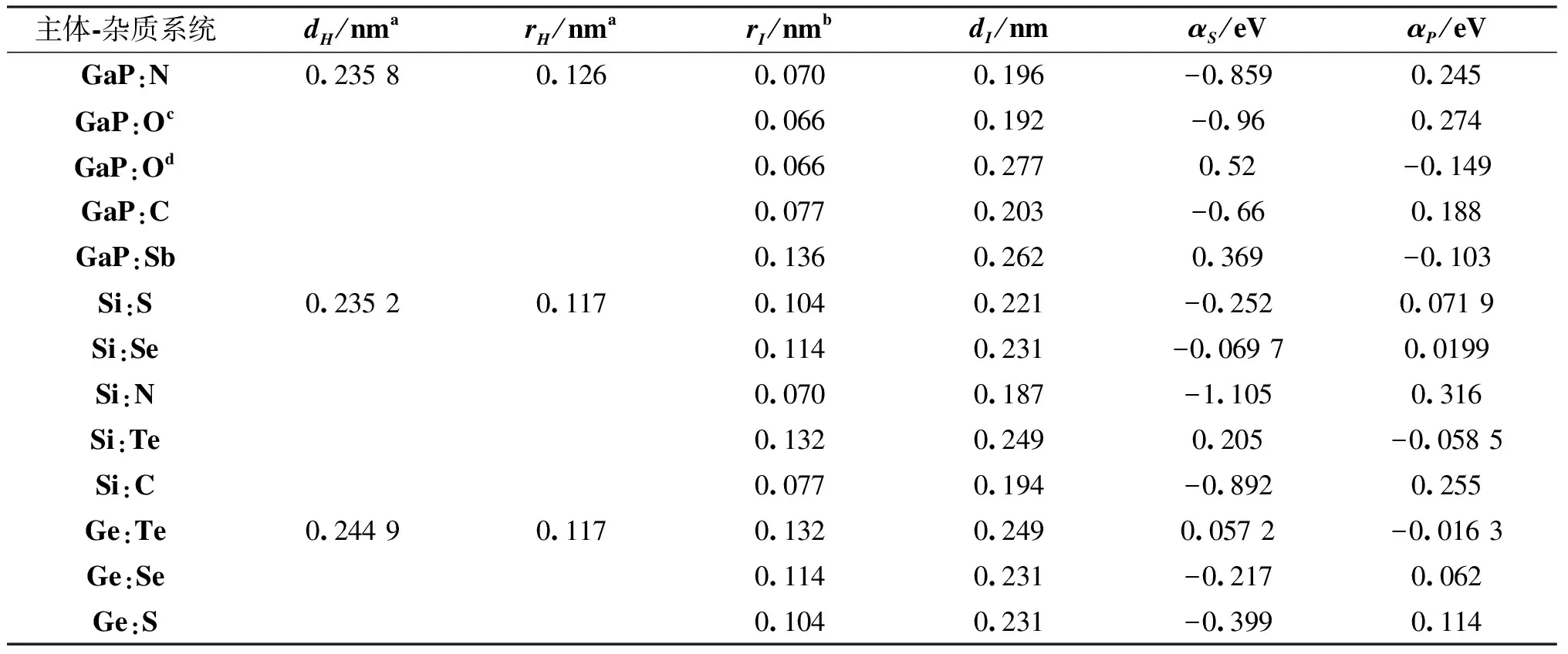
1.2 Baranowski模型
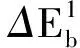
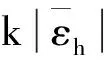
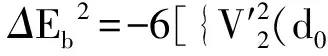

1.3 修正的Baranowski模型计算
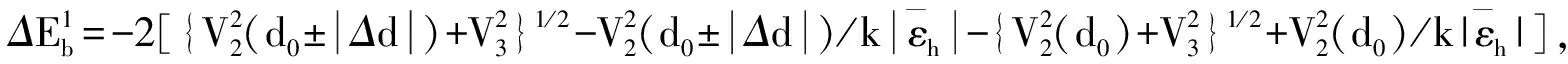
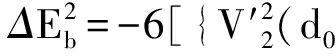
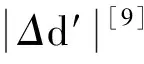
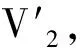

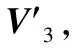

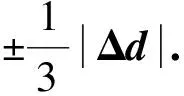
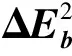
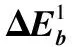

2 总能量

3 结束语

