Duffing方程在两类共振条件下的周期解分支与混沌
蔡美香
(中南林业科技大学数理所,中国 长沙 410004)

(1)
这里δ为阻尼或耗散系数,ηcosΩt为周期阻尼扰动,γx+βx3+αx5为非线性恢复力,fcosωt为周期外力.

本文研究Duffing方程(1)的周期解分支与混沌.与只具有1个周期外力的Duffing方程相比,方程(1)具有3个频率Ω,ω和ω0,当加入第3个频率Ω后,系统的动态有了很大的变化.下面分别在两类共振条件Ω∶ω∶ω0=2∶3∶1和1∶1/2∶1下,研究方程(1)的周期解及其分支存在的充分条件,并应用数值模拟,验证理论分析结果的正确性,以及发现新的动态.
1 在共振条件 Ω∶ω∶ω0=2∶3∶1下的周期解及其分支

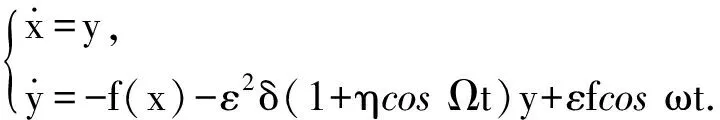
(2)

(3)

(4)


(5)
方程(5)有1个平凡不动点(0,0),非平凡的不动点满足如下方程


由sin2θ+cos2θ=1,令x=r2可得1个关于x的9次方程.由伽罗华理论,5次以上的方程一般不能得出解的解析表达式,因此,令γ=-1,β=2,α=-0.36,f=1,δ=1,Γ=1,可得x0=0.745 356,ω0=1.333 33 ,a2=2.981 42,a3=2.22×10-16,A=-3.416 67,B=-3,C=-2.5,σ=0.093 75,这个9次方程可近似表示为
18 570.4x9+44 278.8x8+(57 607.1-1 414.04η2)x7+(47 950.5-2 512.78η2)x6+
(28 103-2 526.74η2+26.92η4)x5+(11 629.4-1 537.64η2-8.01η3+29.05η4)x4+
(3 388.5-634.69η2-9.64η3+19.31η4)x3+(631.68-161.93η2-6.81η3+5.66η4)x2+
(64.25-24.66η2-2.35η3+0.93η4)x-0.8η2-0.48η3-0.12η4=0.
(6)

图1 当η变化时,方程(6)不动点的分支图Fig.1 Bifurcation diagram of fixed points of Eq.(6) when η varies
图1为方程(6)不动点的分支图,它显示了方程(6)的不动点是如何产生和消亡的.
由平均定理,可得到如下定理.
定理1对方程(2),有
(1)方程(2)无非共振解;
(2)当ηA≤η≤ηB时,方程(2)有1个稳定的共振解;
(3)当η≤ηA和η≥ηB时,方程(2)有3个稳定的共振解;
(4)随着η的增大(减小),当η=ηB时(当η=ηA时),在超临界(次临界)鞍-结分支附近,2个稳定的共振解出现了(消失了);
2 在共振条件Ω∶ω∶ω0=1∶1/2∶1下的周期解及其分支

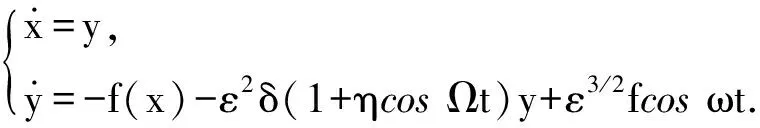
(7)

(8)
令k=1,l=2,同时考虑共振条件Ω∶ω∶ω0=1∶1/2∶1,对方程(8)应用Van Der Pol变换和二阶平均方法,可得二阶平均方程为

(9)


(10)
方程(10)的不动点满足如下方程
(11)


(12)

(i)若Δ′>0,方程(12)有4个实根分别为
(ii)若Δ′<0,方程(12)没有实根;
(iii)若Δ′=0,方程(12)有2个实根分别为
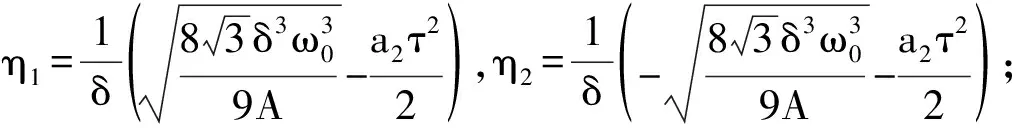
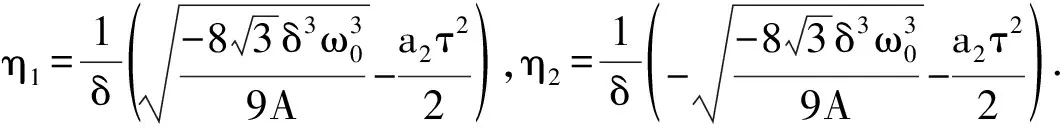

由以上分析可得如下定理.
定理2对方程(7),有


(3)方程(7)的共振解可近似表示为x(t)=x0+εrscos(2ωt+θs)+ε3/2τcosωt+O(ε2),其中(rs,θs)为方程(10)的不动点.
在图2(a)中当Γ=-4时,方程(11)的不动点分支图如图2(b),它显示了共振解的超临界与次临界鞍-结分支以及方程(11)的不动点是怎样出现和消失的.

图2 (a) 共振解的超临界与次临界鞍-结分支;(b) Γ=-4时,方程(11)的不动点分支图Fig.2 (a) Super and subcritical saddle-node bifurcations for resonant solutions;(b) Bifurcation diagram of fixed points of Eq.(11) for Γ=-4
3 对方程(1)的数值模拟
本节分2种情形对方程(1)应用数值模拟,验证理论分析的正确性并发现新的动态.
情形(i):令Ω∶ω∶ω0=2∶3∶1,γ=-1,β=2,α=-0.36,f=1.2,δ=0.2,取未扰动系统的中心(x0,0)=(0.745 356,0)附近的点(0.7,0)为初始值,方程(1)在(η,x)平面的分支图和与之相对应的最大Lyapunov指数图分别如图3(a)和(b).从图上可以看到来自周期3轨的周期2分支到混沌,以及无周期窗口的混沌区域.当η=0.2时的周期3吸引子,当η=2.32时的周期9吸引子,当η=3时的混沌吸引子的相图与Poincare映射图分别如图4(a)~(c)与(d)~(f).

图3 (a) 方程(1)在(η,x)平面的分支图;(b) (a)的最大Lyapunov指数图Fig.3 (a) Bifurcation diagram of Eq.(1) in (η,x) plane; (b) Maximum Lyapunov exponents corresponding to (a)
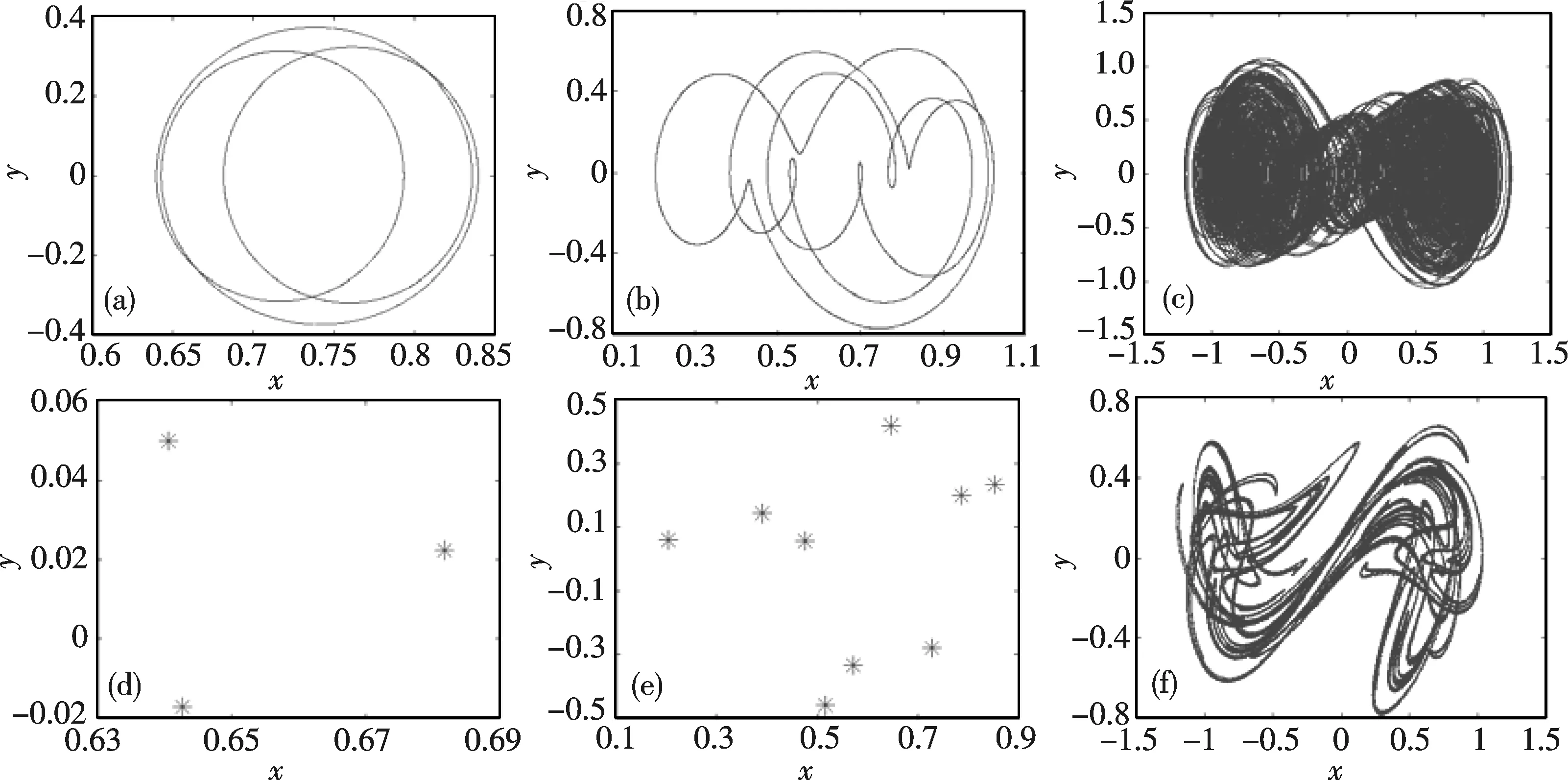
图4 (a)~(c) η=0.2,2.32,3时的相图; (d)~(f) η=0.2,2.32,3时的Poincare映射图Fig.4 (a)~(c) phase portraits for η=0.2,2.32,3; (d)~(f) Poincare map for η=0.2,2.32,3
情形(ii):令Ω∶ω∶ω0=1∶1/2∶1,γ=-1,β=2,α=1,f=1,δ=0.5,取未扰动系统的中心(x0,0)=(0.643 594,0)附近的点(0.6,0)为初始值,方程(1)在(η,x)平面的分支图和与之相对应的最大Lyapunov指数图分别如图5(a)和(b).从图上可以看到当η=0.65和η=5.62时,周期1轨的跳跃行为;当η∈(2.10,2.68),η∈(4.018,4.028)和η∈(4.5,4.58)时,由周期2分支到混沌的过程;当η∈(2.74,2.78)时,由逆周期2分支到混沌的过程;当η≈2.835时,周期2轨突然转变为混沌行为;当η≈3.138时,混沌行为突然收敛到周期3轨;当η≈5.85时,混沌行为突然收敛到周期1轨;当η=2.7,η=5.3,η=6.7时的混沌吸引子的相图与Poincare映射图分别如图6(a)~(c)与(d)~(f).

图5 (a) 方程(1)在(η,x)平面的分支图;(b) (a)的最大Lyapunov指数图Fig.5 Bifurcation diagram of Eq.(1) in (η,x) plane; (b) Maximum Lyapunov exponents corresponding to (a)

图6 (a)~(c) η=2.7,5.3,6.7时的相图; (d)~(f) η=2.7,5.3,6.7时的Poincare映射图Fig.6 (a)~(c) phase portraits for η=2.7,5.3,6.7; (d)~(f) Poincare map for η=2.7,5.3,6.7
4 结论
本文应用常规扰动方法与二阶平均方法,讨论了在2类共振条件下,Duffing方程的周期解及其分支的存在性,并应用数值模拟验证理论分析结果和发现新的动态.结果显示,当加入第3个频率Ω后,二阶平均方程、共振解的近似表达式以及分支情况更为复杂;阻尼扰动项ηcosΩt对方程(1)的整个动态变化有很大的影响.
参考文献:
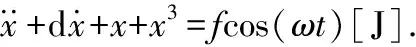
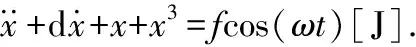
[3] YAGASAKI K. Second order averaging and Melnikov analysis for forced non-linear oscillators [J]. J Sound Vibration, 1996,190(4):587-609.
[4] YAGASAKI K. Detecting of bifurcation structures by higher-order averaging for Duffing’s equation[J]. Nonlinear Dynamics, 1999,18(2):129-158.
[5] LI G X, MOON F C. Criteria for chaos of a three-well potential oscillator with homoclinic and heteroclinic orbits [J]. J Sound Vibration, 1996,136(1):17-34.
[6] HUANG J, JING Z. Bifurcation and chaos in three-well Duffing equation with one external forcing [J]. Chaos, Soliton and Fractal, 2009,40(3):1449-1466.
[7] LAI S, WU B, WANG C,etal. Newton-harmonic balancing approach for accurate solutions to nonlinear cubic-quintic Duffing oscillators [J]. Apply Math Modelling, 2009,33(2):852-866.
[8] NAYFEH A H, BALACHANDRAN B. Applied nonlinear dynamics-analytical, computational, and experimental methods [M]. America: John Wiley and Sons, Inc, 1995.
[9] CHACON R, BEJARANO J D. Homoclinic and heteroclinic chaos in a triple-well oscillator [J]. J Sound Vibration, 1995,186(2):269-278.
[10] CAI M, YANG J. Bifurcation of periodic orbits and chaos in Duffing equation[J]. Acta Math Appl Sinica(English Series), 2006,22(3):495-508.
[11] JING Z, XU P. Chaotic behaviors for Duffing’s equation with two external forcing terms [J]. Progress in Natural Sci, 1999,9(3):171-179.
[12] JING Z, WANG R. Complex dynamics in Duffing system with two external forcing [J]. Chaos, Soliton and Fractals, 2005,23(2):399-411.
[13] JING Z, HUANG J, DENG J. Complex dynamics in three-well Duffing system with two external forcings [J].Chaos, Soliton and Fractal, 2007,33(3):795-812.

