脉冲成形网络负载电磁参数静态分析

杨玉东，王建新

(1. 淮阴工学院 电子与电气工程学院， 江苏 淮安 223001；2.南京理工大学 电子工程与光电技术学院，江苏 南京 210094)

脉冲成形网络(Pulsed Forming Network, PFN)是脉冲功率电源组成的一部分，其主要功能包括能量传输、脉冲整形、功率匹配和调节[1-3]。从脉冲成形网络角度来看，轨道和电枢是其负载，轨道的电感梯度与电阻梯度是负载的两个重要参数，它们的大小与电磁发射效率紧密相关。对负载特性的研究国内外有众多文献涉及[4-6], 它们针对不同的研究目的对负载做不同的等效，文献[4]分析了轨道和电枢中的热能损耗，主要考虑轨道和电枢的电阻分布；文献[5]研究了分布式馈电装置对系统效率的影响，把轨道中的电阻线性化处理；文献[6]分析了电路参数与发射效率之间的关系，把轨道的电感梯度和电阻梯度当作一个定值。上述文献都是从“路”的宏观角度来对待负载特性的，实际上在电磁发射过程中，轨道的电感和电阻随着频率变化也会呈现非线性变化。另外高电压、大电流通过轨道和电枢，其内部的温度、电流密度和电磁场的分布都是不均匀的，这些变化仅靠宏观的电路分析显然远远不够, 对轨道和电枢中物理变化参数求解继续沿袭传统的“路”的模型显得误差过大。为了解电流幅度、频率的变化对负载参数的影响，考虑引入“场”分析方法，以得到较为精确的负载变化模型。

笔者首先建立轨道的二维模型，采用有限元法对轨道中电磁场参数进行求解，然后通过计算轨道中的磁能和热损耗分别计算轨道的电感梯度和电阻梯度随频率变化情况，再通过与经验公式进行比较，寻求获得较高电感梯度的方法。

1 理论和控制方程

从电源角度来看脉冲成形网络的负载是轨道和电枢，电路结构如图1所示。图中PFN为脉冲成形网络，负责给负载提供电能；轨道和电枢为负载，均采用电导率较高的金属(或合金)加工而成，轨道采用高强度绝缘材料进行封装加固做成炮膛，要求轨道和电枢接触面尽可能光滑，电枢与轨道间有一定的机械过盈力以保证彼此之间接触良好。轨道和电枢在频率变化的激励电流作用下，会呈现自感效应、涡流效应、频率趋肤效应、邻近效应等电磁现象。

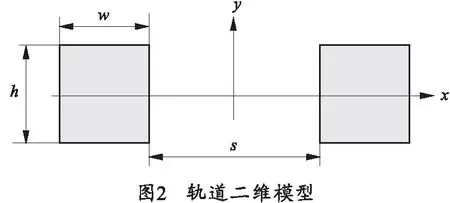
轨道的电感梯度和电阻梯度反映的是单位长度轨道所呈现的电感和电阻，如果轨道材料均匀、形状尺寸规则，则轨道的电感梯度和电阻梯度与轨道的长度无关，因此轨道的模型可以简化为二维模型，如图2所示，图中二维区域即为轨道的轴向横截面，设轨道的尺寸和材料如下：轨道宽w=10 mm，高h=20 mm，轨道间距为s=20 mm，轨道材料为铜。负载的激励电流从轨道的一端加入，流经电枢后从轨道的另一端流出，轨道和电枢采用铜、铝合金等良导体金属材料，在电流传导过程中无自由电荷积聚，因此可以不计位移电流。轨道电磁参数分析基于Maxwell的电磁场理论。脉冲成形网络输出的大多为脉冲电流，由傅里叶分析可知非周期信号可以分解为不同幅度和频率正弦波信号的无限叠加，因此激励电流在负载中形成的电磁场可以用正弦涡流场进行处理。

麦克斯韦方程组涡流场的微分形式为：

(1)

×H=J

(2)

电磁场的本构关系为：

B=μH

(3)

J=σE

(4)

上述各式中，H、B、E、J、σ、μ分别为磁场强度、磁感应强度、电场强度、电流密度、电导率和磁导率。在涡流场中各点场量应满足电磁场的基本方程组。本节考察二维电磁场，即考察轨道横截面中场参数分布情况，设轨道所在的横截面为xy, 激励电流流向为z方向，即垂直于纸面方向，选取矢量磁位A作为未知函数进行求解。引入矢量磁位A的旋度，即：

B=×A

(5)

根据矢量运算法则和库伦规范，经整理得：

(6)

写为时谐场的形式为：

(7)

式中:Js为源电流密度，Js=-σφ；Je为涡流密度，Je=-σ∂A/∂t。上式即为求解涡流场参数的控制方程，加上适当的边界条件和初始条件即构成二维平面定解问题。当求得矢量磁位后即可计算出B和J的分布。求解区域二维网格如图3所示。

2 算法分析

2.1 二维有限元算法分析

设矢量磁位A只有z轴方向分量，即：

A=ezAz

(8)

此时电流密度也只有z轴方向分量，可写为：

J=ezAz

(9)

因此式(7)写成二维偏微分方程形式为：

(10)

式中:Jsz为源电流密度的z向分量，S为求解区域。

求解区域可分为涡流区S1和空气区S2两部分。用有限元法分析的方法之一是根据具体的物理问题构造一个泛函，在定义域内进行剖分插值, 把泛函的变分问题转化为多元函数求极值的问题, 从而得到电磁场定解问题的数值解。式(10)所对应的泛函为：

(11)

式中，F(az)对Az的变分δF(Az)取极小值的解就是所要求的物理解。

2.2 边界条件

上述求解区域S包含涡流区S1和空气区S2。如图3所示，在区域S1内磁导率为4π×107H/m，电导率为1.7×10-8Ω·m；在区域S2内磁导率为1 H/m，电导率为0。涡流区的边界条件为连续条件。对于空气区的边界条件设置，常规分析需要设置Mur或PML吸收边界条件，使场在截断边界无反射，但该问题中轨道间距远小于求解区域尺寸，轨道中电流方向相反，在边界处产生的场相互抵消，可以认为边界上场值为0，即：

ΓS2∶Az=0

(12)

后续仿真结果与文献资料比较证明了该近似方法的可行性。编程即可解得计算区域内Az的分布情况。

2.3 轨道电感梯度求解

设激励电流的方向为z方向，由于求解轨道的电感梯度与激励电流幅度无关，因此为了求解方便，设置流入流出两轨道的电流最大值分别为-1 A和1 A，相位为0，激励频率范围设定为20 Hz～20 kHz。编程求解得到轨道内各点的磁矢位Az，就可以求出各节点的H、B的值，再相应地求解其他需要的参数。

上述二维有限元方法求解得到轨道横截面及周围空间中的场参数分布，沿轨道方向单位长度内轨道及周围空间储存的平均电磁能量WAV可表示为[7]：

(13)

式中:V为二维计算区域在轨道方向单位长度的体积，平均电磁能量WAV与轨道电流的最大值Im、电感量L的关系为：

(14)

则电感梯度为：

(15)

式中:l为单位轨道长度。

3 求解结果与分析

3.1 电磁效应分析

图4和图5分别是激励电流频率为200 Hz和20 kHz时的磁感应强度和电流密度分布图。图中轨道内部电流密度和磁感应强度从内至外逐渐增强，且分布不均匀，两轨道的相邻一侧密度较大。当电流频率为200 Hz时，轨道横截面中心电流密度为9.7×103A/m2，磁感应强度为4×10-8T，最外层边界处的电流密度为1.0×104A/m2，磁感应强度为4×10-5T；当频率达到20 kHz时电流密度分布在轨道的最外层边缘附近，其内部的电流密度几乎为零，在轨道内侧边缘和拐角处磁感应强度达到了6.8×10-5T，电流密度达到了1.36×105A/m2，这是受趋肤效应和邻近效应共同作用的结果。此时激励电流的幅度仅为1 A，而实际电磁发射器的激励电流最大值可以达到105～106A数量级，在轨道的内侧和拐角处的磁感应强度和电流密度将是一个非常大的值，高的电流密度将使轨道内侧的热损耗急剧增加，甚至能达到其材料的熔点引起轨道内侧表面熔解和汽化，进而破坏轨道的平滑度使得轨道变得凹凸不平导致无法再使用。

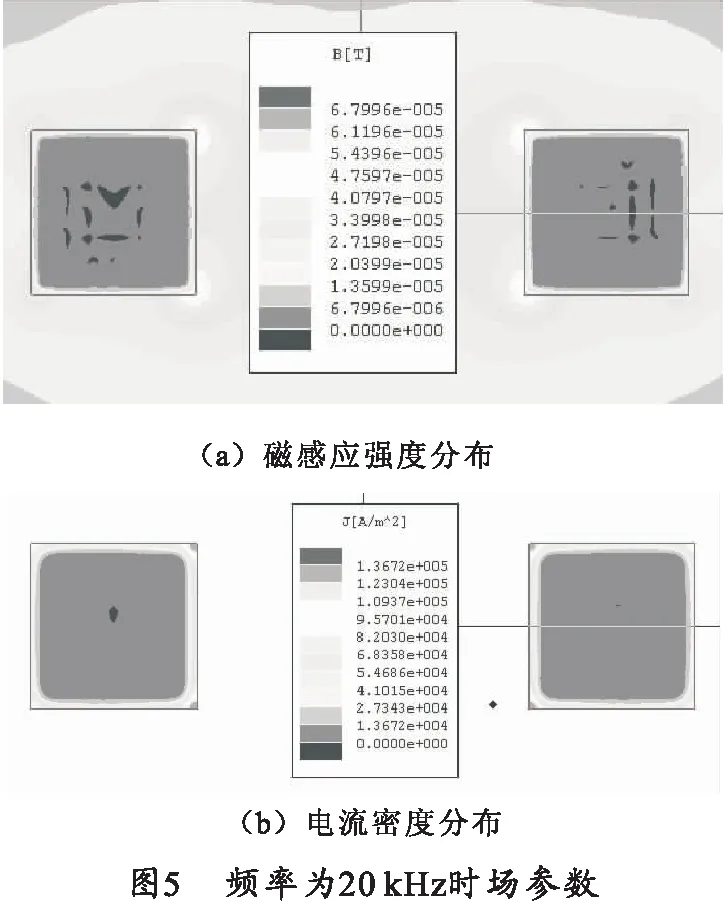
图6是在轨道尺寸一定情况下(参数如图2所示)，根据式(15)求得的电感梯度随频率变化分布情况，结果与文献[8,9]中电感梯度变化的趋势是一致的。

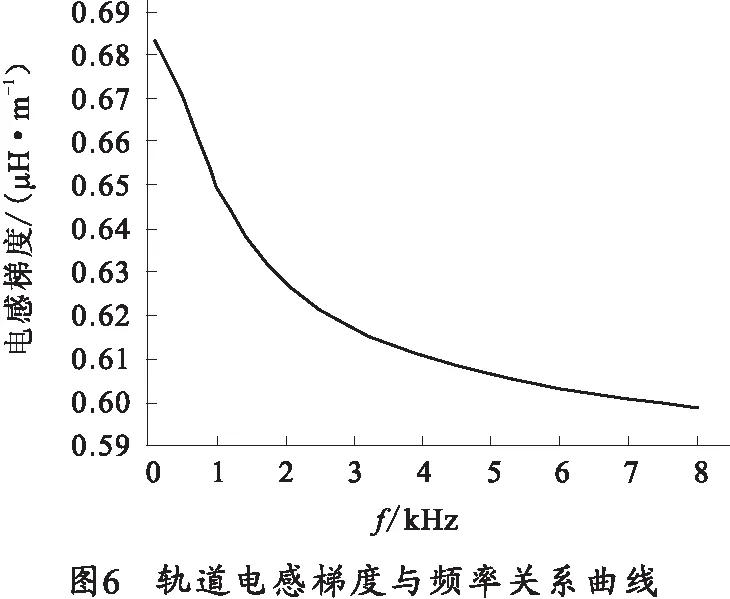
由图6可以看出，频率对电感梯度影响较大。低频(0～1 kHz)电流激励下电感梯度在0.69～0.65 μH/m范围内变化，且随着激励电流频率的升高电感梯度持续下降，当频率为8 kHz时电感梯度下降为0.6 μH/m。上述电感梯度的变化原因也可用电流的趋肤效应来解释，当频率增加时电流趋向于导体的表面流动，内部的磁场减弱，磁场仅围绕在导体的表面使得电感量减小。由前述可知电感梯度下降会造成电磁发射系统效率的降低，因此可以得出如下结论：要提高电感梯度，激励电流应该是平稳无变化的，即恒流激励可使得电感梯度为最大，此时电枢受力均匀、速度增加平稳。但是恒流激励会造成轨道电感储能过大，同样会降低电磁发射系统的效率。因此在脉冲成形网络电路设计时需要考虑激励电流波形的变化，既要得到能够保持较高电感梯度所需要的恒定电流，又要设法使末电流尽可能地降低以便减少电感储能。

3.2 轨道电感梯度与几何尺寸的关系

Asghar Keshtkar 等人提出了一种电感梯度的智能估算公式 (IEM)[6-10]，该方法适用于频率较低的情况，而电磁发射系统中的激励电流频率是变化的，因此IEM近似估计式在频率变化时会存在误差。本文采取有限元计算方法(FEM)，为了与IEM进行比较，激励电流取较低的频率200 Hz。以下是分别采用FEM和IEM方法得到的电感梯度和轨道尺寸的关系。电感梯度与轨道的几何关系如图7所示。

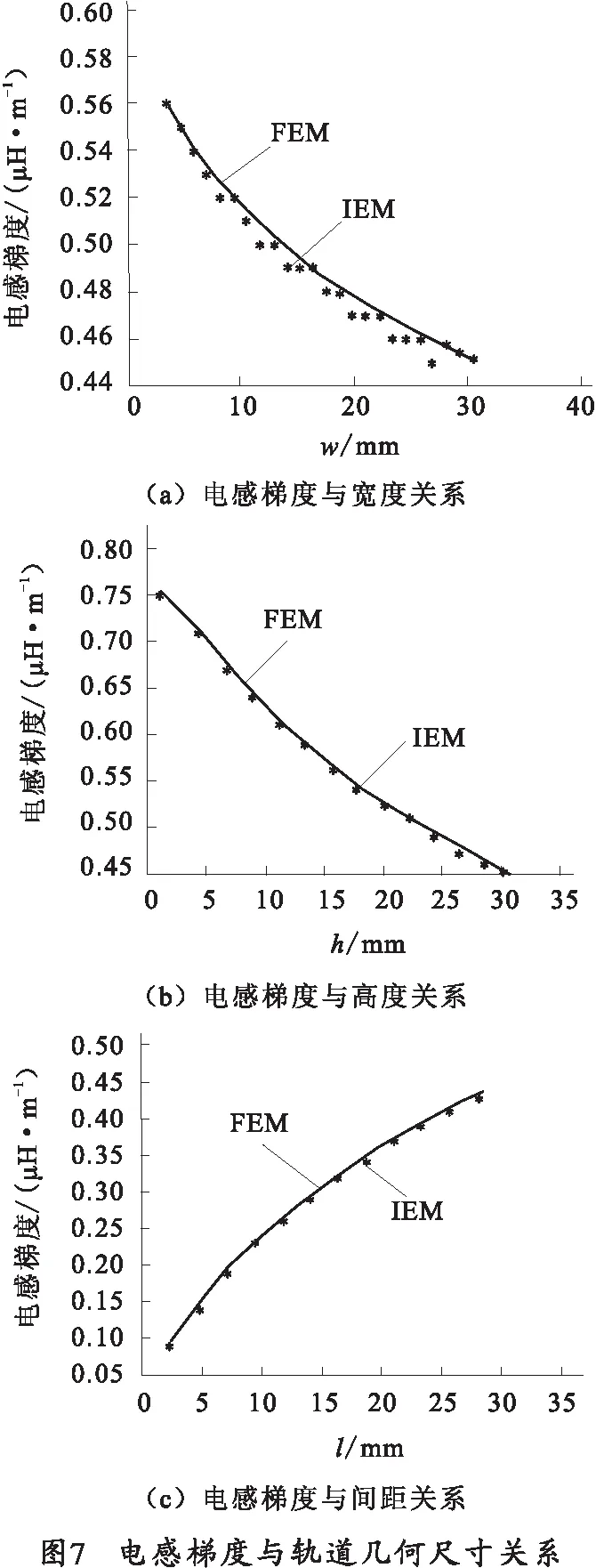
图7中计算的轨道参数与图2参数相同，变化的分别是宽度、高度和间距。由图7可看出，轨道的电感梯度与轨道的尺寸有关系。在轨道高度和间距不变情况下，轨道的电感梯度随着宽度增加而减小；在轨道宽度和间距不变情况下，轨道的电感梯度随着高度增加而减小；在轨道宽度和高度不变情况下，轨道的电感梯度随着轨道间距增加而增加。因此为了获得较高的电感梯度，可以通过减小轨道的宽度和高度、增大轨道间距来获得。当然轨道的高度和宽度不能无限制地减小，考虑到轨道在通过极大激励电流时会受到极大的电磁力，为了有足够的强度，轨道的高度和宽度有一定的限制。另外考虑轨道是电枢滑动的载体，轨道的尺寸还要取决于电枢的尺寸。虽然增加轨道间距也可以增加轨道的电感梯度，考虑到电枢与发射体的尺寸，轨道的间距也不可能做得过大。本文采用FEM方法对轨道电感梯度计算，与此同时计算过程也与IEM方法进行了比较，结果表明两种方法在结果上十分接近，因此在低频电流作用下，可以采用IEM方法进行电感梯度的估算，同时通过此例也证明了有限元法计算电感梯度等负载参数的有效性。

4 结 论

本文主要分析了脉冲成形网络负载静态参数的分布情况。首先推导了轨道的二维涡流场参数求解方程, 建立了轨道的二维有限元模型，求解涡流场中的矢量磁位，再通过计算涡流场的能量求解出轨道的电感梯度随频率变化的分布，同时计算出轨道中磁感应强度、电流密度随频率变化的分布。接着分析了电感梯度与轨道几何尺寸的关系，计算结果与工程经验公式进行了比较，分析得到如下结论：轨道的电感梯度随着频率增加而减小，在较低频率范围内，计算结果与经验公式相吻合。 为提高电感梯度，驱动电流的波形需要尽可能保持平稳。 适当减小轨道的宽度、高度，增加轨道间距，可增加轨道的电感梯度，便于提高电磁发射效率。

[1] 范长增,王文魁.发展中的电磁轨道炮[J].燕山大学学报，2007,9(5):377-379.

FAN Chang-Zeng, WANG Wen-Kui. Review on the electromagnetic railgun[J]. Journal of Yanshan University，2007,9(5):377-379.(in Chinese)

[2] POWELL J D,ZIELINSKI A E.Observation and simulation of solid-armature railgun performance[J]. IEEE Transactions on Magnetics, 1999, 35(1): 84-89.

[3] 李强，范长增.电磁轨道炮轨道和电枢中的焦耳热分析[J].弹道学报,2006, 12(4):39-40.

LI Qiang, FAN Chang-zeng. Rail and Armature Joule Heating of an Electromagnetic Rail Gun[J]. Journal of Ballistics, 2006, 12(4):39-40.(in Chinese)

[4] MANKOWSKI J, Dickens J, et al. A bench top railgun with distributed energy sources[J]. IEEE Transactions on Magnetics, 2007, 43(1):167-169.

[5] THOMAS G,ENGEL J,NERI M, et al. Efficiency and scaling of constant inductance gradient DC electromagnetic launchers[J]. IEEE Transactions on Magnetics, 2006, 42(8): 2044-2047.

[6] KEEFER D,CRAWFORD R,TAYLOR J. Inductance gradient scaling experiments in an augumented railgun[J].IEEE Transactions on Magnetics, 1995, 31(1): 326-331.

[7] KESHTKAT A. Effect of rail dimension on current distribution and inductance gradient[J]. IEEE Transactions on Magnetics, 2005, 41(1): 383-386.

[8] ASGHAR K,SADJAD B,AHMAD K.Derivation of a formula for inductance gradient using intelligent estimation method[J].IEEE Transactions on Magnetics,2009,45(1):305-308.

[9] KEEFER D,CRAWFORD R,TAYLOR J. Indu ctance gradient scaling experiments in an augumented railgun[J]. IEEE Transactions on Magnetics, 1995, 31(1): 326-331.

[10] LANDEN D,SATAPATHY S. Eddy current effects in the laminated containment structure of railguns[J]. IEEE Transactions on Magnetics, 2007, 43(1): 150-156.