基于RecurDyn的链式回转弹仓多边形效应分析

解凤娟,何宗颖,骆小平,孙大鹏

(西北机电工程研究所，陕西 咸阳 712009)

链条传动的多边形效应是指当链条的主动链轮以定角速度转动时，从动链轮的转速以及链条的速度均是不恒定，而是呈现出周期性变化，这主要是由于节圆和节线的多边形不重合导致的，如图1[1]所示，当主动链轮以速度vA转动时，链条水平速度v发生周期性变化，当链轮转过一个链节时，速度的变化为一个周期[2]，其计算公式为：

v=vA cosβ

式中，v为链条速度;vA为主动链轮的线速度;T为链条速度变化周期;N为主动链轮转速(r/min);n为链轮齿数。

大口径火炮由于弹丸质量较大，尺寸较长，人员不易操作，因而多采用自动供弹装置[3]。链式回转弹仓具有结构紧凑、传动效率高等优点，在大口径火炮供弹装置中应用较多。某弹仓采用链式回转原理的结构设计，结构紧凑，采用了3齿链轮，其回转运动的多边形效应比较明显[4]。

RecurDyn软件是专业的多体动力学仿真软件，非常适合于求解大规模及复杂接触的多体动力学问题[5]。

通过对比分析RecurDyn软件,计算出弹仓的不同数据和图形，选择合适的方案，减小多边形效应在弹仓运动中的影响。

1 弹仓建模

1.1 弹仓模型建立

由于RecurDyn软件建立复杂装配模型不如UG方便快捷，本文将通过UG分别建立弹仓各组成部件的三维模型，如图2所示，弹仓主要由弹筒、套箍、弹架导轨、主动和从动链轮等组成，之后按照相应的装配关系完成弹仓的装配模型，将该模型转成*.x_t格式导入到RecurDyn软件中。

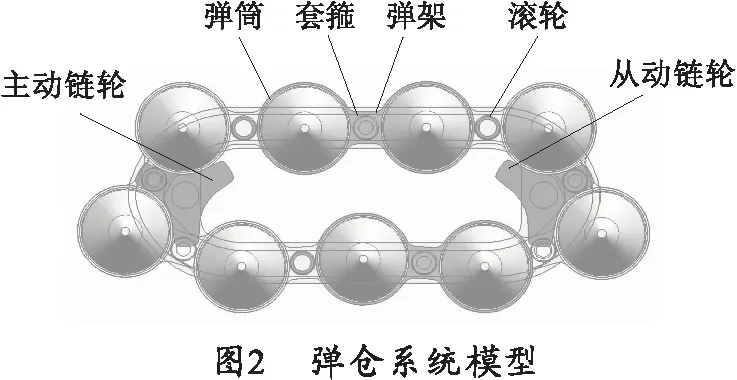
弹仓回转虽然采用的是链式传动原理，但由于弹筒和套箍的结构复杂，与标准的链节和铰接轴区别较大，因此无法直接调用RecurDyn软件中的chain(链条)模块，必须直接单独给各个组件定义约束和接触，具体定义如下：弹架定义为固定副、主、从动链轮与弹架为铰接、弹筒与套箍为铰接、滚轮与套箍为铰接、滚轮与弹架轨道为面接触、滚轮3齿面与相应的弹筒面为面接触，各接触面均设定为相同材质的材料(钢)，各组件受重力情况与实际情况相同。根据实践经验，碰撞接触参数选取如表1所示。

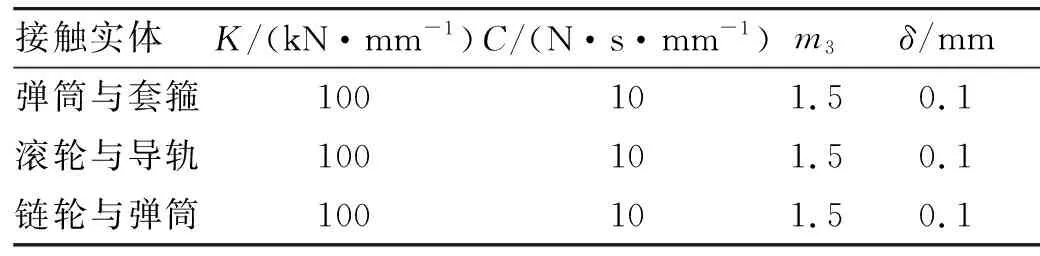
表1 弹仓模型动力学模型参数设置[5]

1.2 基于RecurDyn软件的接触力理论

在RecurDyn软件中，物体之间的接触力公式[5]为：

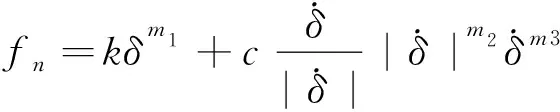
这些参数的取值取决于材料的类型和尺寸。

1.3 仿真分析

添加弹仓各组件的约束后，定义链轮转动副的驱动，之后进行运算求解，运算成功后，可直接查看弹仓的实时运动情况，应用Recurdyn软件的后处理，可输出所需要的曲线和数据，进行对比分析。

2 不同相位时的速度和扭矩变化

针对如图2所示的弹仓模型，分别按照相同相位和最大不同相位进行布置，相同相位即两链轮在回转时其3个齿的位置完全相同(即图2所示)，最大不同相位是指两链轮在回转时其3个齿处于180°的位置(如图3所示)。

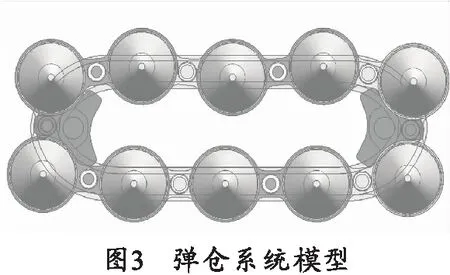
分别建立两种情况的三维模型，为了提高计算速度，简化模型，用尽量少的链节，因而装配时同相位只用9个筒子装配，不同相位时只用10个筒子装配，之后将模型输入到RecurDyn软件中，设置相同的约束和接触条件，均定义主动轮以10 r/min分的速度匀速转动，为减小仿真运算时间，只计算链轮转动2个弹距的时间，即链轮转动240°，由转速可以计算出这个时间为4 s。

经过运算，两个装配体的运动按照预想的运动轨迹运行，对运算结果进行后处理，可以分别得到链条水平速度曲线和主动链轮的输入扭矩曲线。链条水平速度曲线反应了水平轨道上弹筒的水平运动速度随时间变化的情况，输入扭矩曲线反应了主动轴运动时所需扭矩的变化情况，这两条曲线直接反应了运动的稳定性，也即多边形效应对弹仓运动的影响。

图4、图5分别为同相位和最大不同相位时的链条水平速度曲线。从图4可以看出，主、从动链轮同相位布置时弹仓运动的速度曲线变化较缓，数值波动小，周期T在2 s左右，与理论计算值相符，速度在80～180 mm/s之间呈余弦式周期变化。从图5可以看出，主、从动链轮最大不同相位布置时弹仓的运动速度波动比较大，变化的周期不易读出，速度在40～240 mm/s之间变化。

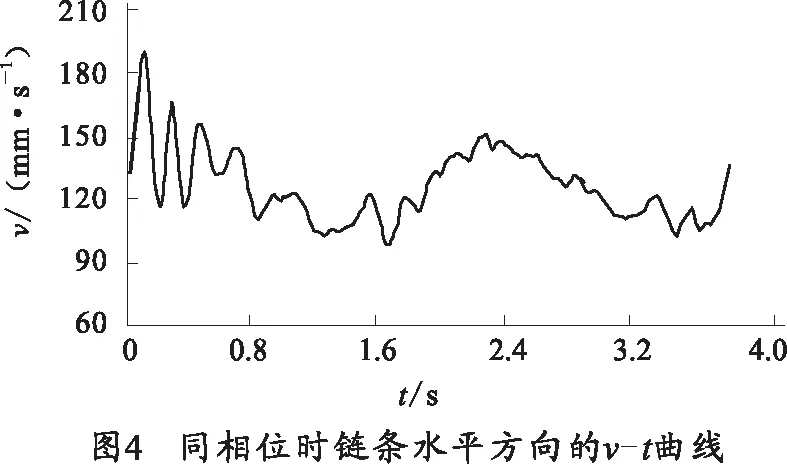
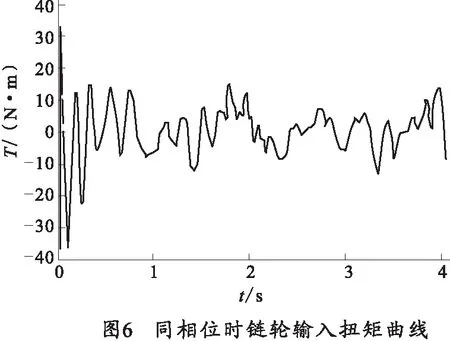
图6、图7分别为同相位和最大不同相位时的主动链轮输入扭矩曲线。从图6可以看出，同相位布置时弹仓的输入扭矩在开始时出现了1次震荡，之后逐步趋于稳定，大致在20 N·m以内波动。而从图7可以看出，最大不同相位布置时主动链轮的输入扭矩数值较大，在170 N·m以内，并且波动一直比较大。

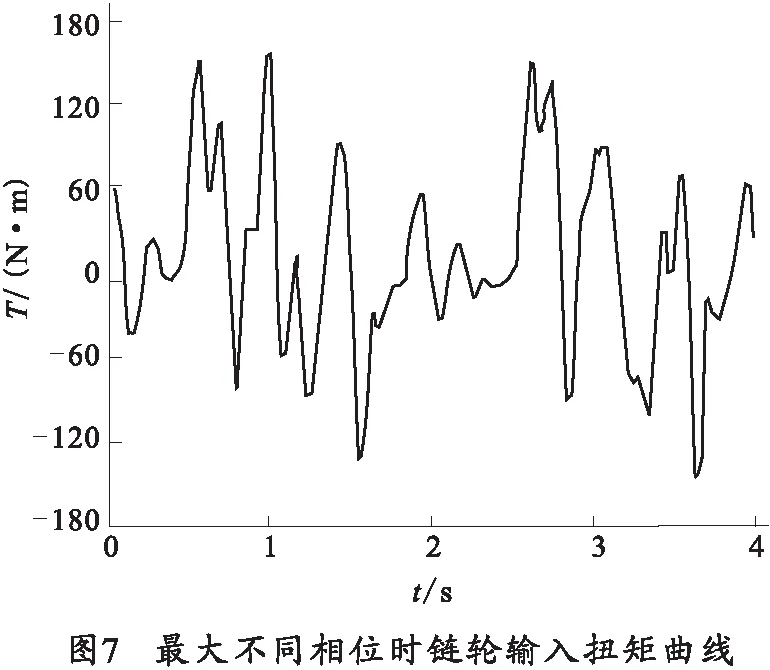
以上分析可以得出，大节距、齿数少的链式回转弹仓按照主、从动链轮相同相位的方式布置时，可减小多边形效应引起的速度波动和弹仓输入扭矩波动。

相位是否相同的选择规律是：若(n-Z)是偶数，则两链轮为同相位布置，若(n-Z)是奇数则两链轮为最大不同相位布置， 其中n是链节数即是弹筒数，Z是链轮齿数。

3 不同驱动时的速度和扭矩变化

采用上述相同相位3齿链轮传动的弹仓模型，并且定义相同的约束和初始环境，不同的是本次计算设定主、从动链轮均是以10 r/min的速度匀速转动，采用两链轮同时驱动弹仓回转。经过运算后，由于主、从动两链轮扭矩曲线和速度曲线完全相同，所以本文只列出了1个轴的扭矩和速度曲线，分别如图8和图9所示。

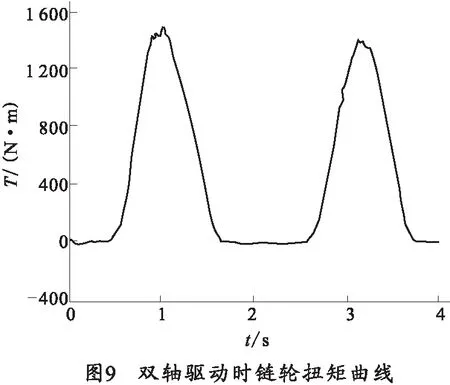
从图8和图9可以看出，双轴驱动时，弹仓转动周期T数值在2 s左右，与计算值相符，链条水平速度在60～140 mm/s之间余弦式周期变化，弹仓转动时单个链轮所需的扭矩在0～140 N·m之间变化，弹仓所需要的总扭矩是双链轮扭矩之和，即是0～280 N·m之间变化。

与同相位单轴驱动弹仓的运算曲线(图4和图6)相比，两者有如下区别：

1)对比图4和图8速度曲线可知，两者速度幅值大致相同，但是双轴驱动的速度跳动较大，运动的平稳性不如单轴驱动弹仓的平稳性好；

2)对比图6和图9扭矩曲线图可知，双轴驱动弹仓回转所需要的总扭矩远远大于单轴驱动所需要的扭矩值，其原因可能是因为双轴驱动会导致链条过紧，需要更大的输入扭矩。

通过比较可以看出，链式回转弹仓选用双轴驱动的方式并不能减小多边形效应的影响，并且会导致输入扭矩大大增加，因此在设计时，在满足动力要求的前提下，应优先选用主动链轮单轴驱动的方式。

4 结束语

本文应用RecurDyn软件对链式弹仓的运动进行仿真分析，可直观地认识链条传动的多边形效应，并且明确了主从链轮具有相同相位布置，以及采

用单轴驱动时对减小弹仓回转运动的多边形效应具有较好的效果，此结论对链式回转弹仓的设计起到了一定的指导性作用。目前仅对上述两方面进行了分析，对链轮齿数、链轮节距、弹筒总节数等方面对弹仓多边形效应的影响规律还未进行仿真分析，有待更进一步的研究。

[1] 梁志民，安宗文，李朝晖，等.链速补偿机构设计[J].甘肃工业大学学报.2003(2)：47-49.

LIANG Zhi-min AN Zong-wen LI Chao-hui et al .Design of compensating mechanism of chain velocity[J].Journal of Gansu University of Technology，2003(2)：47-49. (in Chinese)

[2] 《机械设计手册》编委会. 机械设计手册：第2卷[M].3版.北京:机械工业出版社，2005：14-81.

Editorial committee of mechanical design handbook.Mechanical design handbook:second volume[M].3rd ed.Beijing:China Machine Press，2004:14-81. (in Chinese)

[3] 梁辉，马春茂，潘江峰，等.大口径火炮弹药自动装填系统现状和趋势[J].火炮发射与控制学报，2010(3)：103-107.

LIANG Hui,MA Chun-mao，PAN Jiang-feng，et al.Current situation and development trend of autoloader in large caliber howitzer[J]. Journal of Gun Launch & Control,2010(3)：103-107.(in Chinese)

[4] 张玲玲，陆天炜， 吴鹿鸣，等. 链传动多边形效应的实验研究[J].机械工程与自动化，2010(8)：97-99.

ZHANG Ling-ling， LU Tian-wei， WU Lu-ming，et al. Experimental study on the polygon-effect of chain-transmission[J].Mechanical Engineering & Automation,2010(8)：97-99. (in Chinese)

[5] 郑建兴，张相炎.基于RecurDyn的同步带弹箱动态特性仿真研究[J].火炮发射与控制学报，2010(4)：75-78.

ZHENG Jian-xing，ZHANG Xiang-yan.Dynamic characteristic research of timing belt ammunition box based on RecurDyn[J].Journal of Gun Launch & Control，2010(4)：75-78.(in Chinese)