反后坐装置安装方式对密集度影响分析

高 波，郁永年，高 飞

(1.63961部队,北京 100012;2.西北机电工程研究所，陕西 咸阳 712099;3.驻咸阳地区军事代表室，陕西 咸阳 712099))

在火炮射击过程中，摇架的变形和运动是影响密集度的主要因素之一。

由于火炮的射击载荷通过反后坐装置传递给摇架，摇架的变形和运动又反过来又影响炮身的运动，因此反后坐装置的设计和在摇架上的安装方式的确定是火炮设计的一个重要环节[1]。降低后坐阻力，保证火炮后坐运动的一致性在国内文献中多有描述，但反后坐装置在摇架上的固定方式讨论很少。

本文通过对摇架变形及其与反后坐装置相互作用的分析，阐述了反后坐装置在摇架上不同安装方式的利弊，提出了后固定的观点，并结合测试数据进行了说明。

1 基本设计要求

摇架在火炮发射过程对后坐部分具有支撑和导向作用，可以把火药气体13 ms时间内300～500 t膛底压力通过反后坐装置转换为0.1～0.3 s时间内10～40 t的后坐阻力。假定火炮架体强度满足射后不产生永久形变的要求，要实现火炮发射对弹丸的起始扰动小、炮口点章动一致，首先要求架体(包括摇架)在弹丸膛内时期的弹性变形尽可能小，其次要求反后坐装置施加于架体的后坐阻力尽可能一致，第三要避免膛内时期高低机支反力产生换向，最后要求反后坐装置在摇架中的布置要合理[2]。

架体(包括摇架)在弹丸膛内时期的弹性变形尽可能小，一方面需要通过优化结构、增加重量来提高架体(包括摇架)刚度，另一方面可以通过调整反后坐装置设计、降低驻退机后坐阻力来减小变形。

反后坐装置施加于架体的后坐阻力尽可能一致，需要优化驻退机设计，特别是火炮连续射击，驻退液温度变化的条件下，应保证液量调节器有效、可靠工作。

避免膛内时期高低机支反力产生换向，需要通过合理设计和炮尾配重调整e值的大小和正负，做到平衡机力矩、后坐阻力矩、惯性力矩三者作用的方向一致，保证U力在膛内时期方向一致。

反后坐装置在摇架中的合理布置，既涉及到摇架本身的刚强度设计，又关系到平衡机、驻退机、复进机、炮身、上架与摇架的相互装配关系，对火炮发射落弹散布的影响不可忽视。因此，摇架设计一方面要通过优化结构保证摇架本身的刚强度足够大，在装配前后和发射过程产生的弹形变性控制在设计要求范围，保证后坐各部分运动平稳顺畅；另一方面要防止后坐阻力对摇架本体产生影响，特别是后坐阻力逆向传导至摇架的前端，前后端变形不一致使得身管指向脱离初始位置，弹丸出炮口瞬间初始扰动加剧、章动角增大，散布变差[3-5]。

2 反后坐装置与摇架连接方式对后坐运动的影响分析

图1和图2分别是某型火炮摇架本体和反后坐装置装配示意图，假定摇架主筒前后铜套和平衡机支臂刚强度足够，炮身在摇架内没有因架体变形而产生的运动阻滞，单独讨论反后坐装置与摇架连接对发射后坐的影响。

图3为简化后的摇架结构示意图，前后套箍用以连接驻退机，炮身护筒用以支撑炮身，肩部为前后套箍和炮身护筒的连接部分，在此作为重点进行分析。

驻退杆通过深孔与炮尾刚性连接，随着炮身的后坐一起运动，由于炮尾同时连接火炮身管和退机驻退杆，其刚度完全可以保证驻退杆的运动和身管保持平行，也就是说驻退杆被强制沿身管轴线运动。驻退杆后坐带动活塞压缩液体形成高达35 t的后坐阻力，作用于筒端并通过后套箍肩部传递至摇架耳轴。下面就前后套箍与反后坐装置的不同连接方式进行分析。

2.1 前后套箍同时采用固定约束

前后套箍与驻退机同时采用固定连接(见图4)，这种连接方式必须做到后套箍肩部刚度足够大以保证后套箍不产生位移变形，后坐阻力不会通过驻退机筒传递到前套箍，前后套箍相对位置保持稳定，可以保证驻退机正常运动。如果后套箍肩部受力变形，就会通过固连的驻退机筒把后坐阻力传递到前套箍，由于前套箍肩部连接刚度和后套箍存在差异，势必会引起变形不一致，导致炮身护筒前端位置发生改变，特别是前套箍刚度较弱时会通过套筒带动身管指向的变化，影响火炮射击的密集度。

因此，只有在后套箍刚度设计足够大不产生变形或前后套箍刚度相同变形一致的情况下，采用前后套箍对驻退机同时进行固定连接，可以保证驻退机工作正常且不会对身管的指向产生影响。在实际结构上，由于后套箍受力后的变形不可避免，而前后套箍因结构不同，产生的变形大小也各不相同，再加上驻退机筒刚度的影响，很难保证前后套箍变形的一致性。

2.2 后套箍采用固定约束且前套箍完全解除约束

后套箍采用固定约束且前套箍完全解除约束(见图5)，发射后坐过程中，后套箍在后坐阻力的作用下出现“仰起”现象，带动驻退机筒向上运动，如某火炮驻退机筒因后套箍变形轴线上仰计算值约0.4°，导致前端上仰最大可达11.6 mm。而参与后坐的驻退杆被强制沿身管轴线运动，与驻退机筒接触的活塞会下压限制驻退机筒的抬升，活塞与驻退筒内壁之间的压力增大，摩擦阻力增加，拆检后会发现，在驻退筒内壁下表面和活塞铜头下表面磨损大于上表面，活塞铜头下部前端磨损较后端严重。

2.3 后套箍采用固定约束且前套箍轴向解除约束

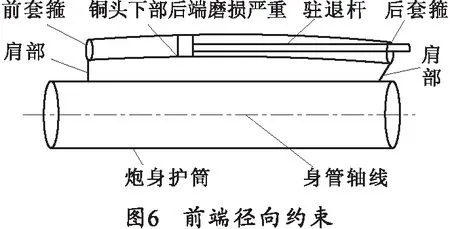
后套箍采用固定约束且前套箍轴向解除约束(见图6)，发射后坐过程中，后套箍在后坐阻力的作用下出现“仰起”现象，带动驻退机筒一方面向后运动，另一方面向上抬起。由于前套箍轴向约束解除，驻退筒后移不受限制，但前套箍径向约束使得驻退机筒向上抬升无法实现，后坐过程驻退机筒就会出现“弓背”现象，筒径水平方向变宽、垂直方向变窄，当参与后坐的驻退杆被强制沿身管轴线运动时，与驻退机筒接触的活塞会下压抚平驻退机筒的拱起并克服由此引起的变形，活塞与驻退筒内壁上下之间的压力增大，摩擦阻力增加，拆检后会发现在驻退筒内壁下表面和活塞铜头下表面磨损大于左右两侧表面，活塞铜头下部后端磨损较前端严重。

3 前后套箍同时采用固定约束以提高摇架刚度设计误区分析

由于摇架是火炮后坐运动部分的安装机构，变形量的大小与炮身运动一致性直接相关，刚强度设计显得尤为重要。为了提高摇架的刚度，设计中利用反后坐装置驻退机和复进机外筒的前后端与摇架前后套箍同时固定连接，或者另外增加反后坐装置护筒，示意见图4。这种连接必须做到后套箍肩部刚度足够大保证后套箍不产生位移变形，后坐阻力不会通过驻退机筒传递到前套箍，前后套箍相对位置保持稳定，可以保证驻退机正常运动。如果后套箍肩部受力变形，就会通过固连的驻退机筒把后坐阻力传递到前套箍，由于前套箍肩部连接刚度和后套箍存在差异，势必会引起变形不一致，导致炮身护筒前端位置发生改变，特别是前套箍刚度较弱时会通过套筒带动身管指向的变化，影响火炮射击的密集度。

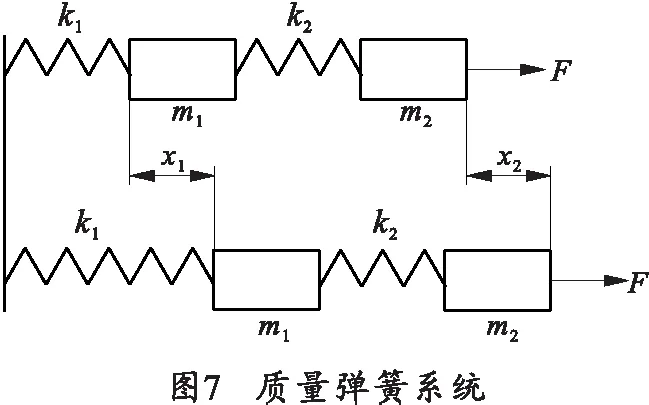
对上述结构建立力学模型说明如下。图7所示为典型质量-弹簧系统。

4 结 论

按照上述分析，改变反后坐装置与摇架连接方式，将原来的前后套箍同时采用固定约束改为后套箍采用固定约束且前套箍轴向解除约束，并在前套箍增加径向间隙，最大射程地面密集度横向散布和纵向散布基本稳定在要求范围，改进效果非常明显。作为一致性考核的密集度试验的基本要求是射击条件(包括火炮、弹药、阵地、气象等)保持一致。对火炮而言，需要重点关注反后坐装置的设计和安装方式，通过降低驻退机最大后坐阻力达到减小架体弹性变形、提高架体刚度的目的，保证驻退机液量调节器在驻退液温度变化情况下可靠而有效工作，保证每次后坐运动规律的一致性，进而实现膛内时期火炮和弹丸之间相互作用一致，尽可能做到弹丸出炮口瞬间的初始扰动稳定一致。

[1] 张月林．火炮反后坐装置设计[M]．北京：国防工业出版，1984:308-341.

ZHANG Yue-ling．Design of gun recoil mechanism[M]．Beijing：National Defense Industry Press，1984:308-341．(in Chinese)

[2] 洪嘉振．计算多体系统动力学[M]．北京：高等教育出版社，1999．

HONG Jia-zhen．Calculation multibody system dynamics[M]．Beijing：Higher Educatian press，1999．(in Chinese)

[3] 杨玉良，秦俊奇，狄长春，等．炮口强冲击条件下的身管稳定性校核研究[J]．火炮发射与控制学报，2011(2)：43-46．

YANG Yu-liang，QIN Jun-qi，DI Chang-chun，et al．Checking research on barrel stability under muzzle strong impact[J]．Journal of Gun Launch & Control，2011(2)：43-46．(in Chinese)

[4] 王靖军，赫信鹏．火炮概论[M]．北京：兵器工业出版社，1992：122-126，204-207．

WANG Jing-jun，HE Xin-Ping．Conspectus of gun[M]．Beijing：The Publishing House of Ordnance Industry．1992：122-126，204-207．(in Chinese)

[5] 王宝元，董文祥，邵小军．火炮结构结合面力学模型研究综述(Ⅰ)[J]．火炮发射与控制学报，2011(1)：89-92．

WANG Bao-yuan，DONG Wen-xiang，SHAO Xiao-jun．Review and prospect of the research on the gun structure joint surfaces in mechanical model(Ⅰ)[J]．Journal of Gun Launch & Control，2011(1)：89-92．(in Chinese)

[6] L.米罗维奇．振动分析基础[M]．上海交通大学理论力学教研室，译．上海：上海交通大学，1982：5-15．

L.Merirovitch．Elements of vibration analysis[M]．Shanghai Jiaotong university theoretical teaching and research section，translated.Shanghai:Shanghai Jiaotong University,1982:5-15.(in Chinese)

[7] 李惠彬．振动理论与工程应用[M]．北京：北京理工大学出版社，2006：130-144．

LI Hui-bing．Theory of Viberation and Engineering Application[M]．Beijing：Beijing Institute of Technology Press，2006：130-144．(in Chinese)