弹药自动装填机械手运动学分析

李郁峰，潘玉田，李魁武，李贵虎

(1.中北大学 信息与通信工程学院，山西 太原 030051；2.西北机电工程研究所,陕西 咸阳 712099；3.山西北方机械制造有限责任公司，山西 太原 030009)

弹药自动装填机器人技术的研究是无人化作战平台的关键技术之一，研究能满足大口径火炮射速要求、实现任意角度装填、弹种自动识别和选择、弹丸和装药自动供给和输送入炮膛的自动装填机器人系统，对于火炮武器系统无人化的实现具有十分重要的意义[1]。

1 结构及工作原理

1.1 总体布局

自动装填机械手安装在炮塔旋转盘或吊栏上，位于火炮后下方，确保机械手在初始位置时位于火炮后坐范围之外。机械手手抓推进器抓持弹或药后，弹药的轴线和输弹槽轴线位于同一个平面内。在这个平面上，炮尾输弹槽的运动区域是以耳轴为圆心、炮尾到耳轴距离为半径的一部分圆弧，这段圆弧上的各个位置点即为机械手的目标位置[2]。自动装填机械手在整个自动装填系统中的位置如1图所示。

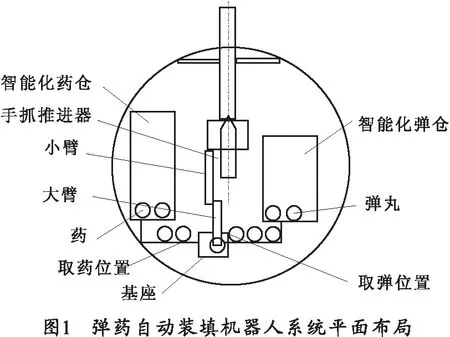
1.2 动作流程

弹药自动装填机械手的任务是完成弹和药的自动装填任务。自动装填机械手的动作流程如图2所示。当主控机给出供弹指令后，弹仓内的弹链转动，经选弹后，将弹丸输送至出弹仓口，传弹器将弹丸从弹仓传出至取弹位置，机械手手抓推进器的两个手爪同时夹紧炮弹。关节驱动电机开始驱动3个俯仰关节使机械手按规划的路径将弹送至炮尾输弹槽后端，并使炮弹轴线与炮膛轴线重合。主控机给出输弹指令，手爪推进器的液压缸驱动握持手爪进行强制输弹操作。输弹结束后，主控机给出供药指令，并通过驱动小臂中间的偏转关节将手抓推进器转换到药仓的一侧，药仓后部的传药器将药传到取药位置，机械手手抓夹紧装药后，再驱动小臂中间的偏转关节将手抓推进器转换到弹仓一侧，重复以上装填弹丸的动作完成装药的自动装填任务。整个工作过程中不允许装填机械手有大的摆动，要求它能把弹(药)准确运送到-5°～70°的任何位置[3-4]。

1.3 结构模型

自动装填机械手主要由固定基座、大臂、小臂和手爪推进器等几部分组成，为5自由度的机械手结构。基座和大臂之间的转动副联结构成了第1俯仰关节，大臂和小臂之间的转动副联结构成了第2俯仰关节，这两个转动关节由电机驱动将弹(药)从初始位置输送到炮尾输弹槽，用于控制机械手手抓推进器的位置；小臂和手爪推弹器之间也为转动副联结，构成了第3个俯仰关节，由电机驱动使炮弹的轴线和炮膛轴线相重合，用于控制机械手手抓推进器的姿态；手爪推进器上的手爪和导槽之间为平动副联结，由液压缸驱动手爪推动炮弹沿着炮膛轴线平动，用于完成输弹(药)动作。小臂中间的偏转关节，用于装填弹和药之间的转换[5-6]。所有转动关节都由步进电机经谐波减速器进行驱动。整个自动装填机械手机构、弹仓、药仓及火炮随炮塔一起转动。

1.4 连杆坐标参数

按照弹药自动装填机械手的整个动作过程的任务要求及炮塔的空间尺寸结构，定义机械手的总体尺寸，给出自动装填机械手的总体指标。弹药装填机械手的大臂、小臂和手腕恰好可视为三动杆机构，其中小臂中间的偏转关节，仅用于装填弹和药之间的转换，手爪推进器上的手爪和导槽之间的平动关节，仅用于完成输弹(药)动作。因此该自动装填机械手机构可简化为平面3自由度串联机构。根据三动杆机构的性能图谱，当L1∶L2=1～1.2且L3<0.5时,三动杆机构的灵巧性、灵活度和运动幅度较高[7-8]。按照D-H法可对机械手模型建立如图3所示的的坐标系。根据建立好的连杆坐标系，可得到如表1所示的连杆参数。

表1 弹药自动装填机械手连杆及关节参数

2 运动学分析

2.1 运动学正问题

正向运动学主要解决机器人运动学方程的建立及手部位姿的求解问题。正向运动学的解是唯一确定的，根据图3在此机器人模型上建立的连杆D-H坐标系以及表1所示连杆参数，建立运动学方程。对于平面关节机器人，由坐标系{i}到{i-l}的变换正向求解的齐次变换矩阵记作：

(1)

现在，将机器人的参数带代入式(1)，得到第3坐标系相对于基座坐标系位姿的齐次变换矩阵：

(2)

其中:c123=cos(θ1+θ2+θ3)，s123=sin(θ1+θ2+θ3)

nx=c123ox=-s123ax=0px=l1c1+l2c12+l3c123

ny=s123oy=-c123ay=0py=l1s1+l2s12+l3s123

nz=0oz=0az=1pz=0

(3)

所以

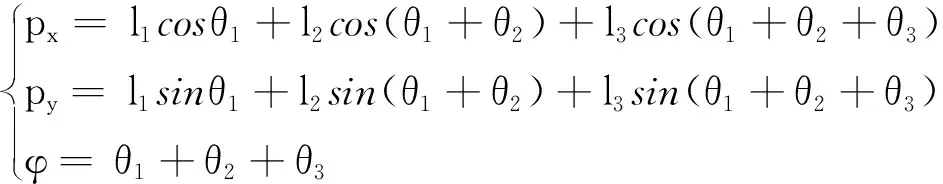
(4)

2.2 运动学逆问题

机器人运动学逆问题就是已知末端连杆的位置和方位，求得机器人的各个关节变量。在机器人控制中，只有使各关节移动或转动到逆解算出的值，才能使末端执行器达到工作所要求的位置和姿态。运动学反解的方法很多，这里用代数法求解，在求解方程时解的形式已经确定[9]。

所以已知px，py,φ,求解方程式组(4)，即可求得各关节变量。

求解关节变量的方程式如下：

(5)

其中:

(6)

式中的正负号表示有2个可能的解，这样组合起来的话，可能有许多组解，但是由于结构的限制，有些解不可能实现，所以要选1组最适合的解，来满足机械手的工作要求。

3 运动学仿真

3.1 构建模型

弹药自动装填机械手仿真模型通过手动驱动滑块或输入关节变量的值，来改变机器人末端位姿，从而直观地显示机器人的运动，可以观察生成的控制面板上末端位置是否和正运动方程计算得到的值相同，并且可拖动滑块来改变各个关节的转角来验证运动副的设置是否正确[10-11]。

3.2 正运动学仿真

利用Robotics Toolbox中的fkine函数可以实现机器人运动学正问题的求解。要实现两点之间的运动，首先要创建一个时间向量，假设在2 s内完成某个动作，采样间隔是50 ms，来实现两点之间的轨迹规划[12]。由式(4)运动学方程可计算出两组关节变量对应的机器人手臂末端点。在图5建立了机器人手臂仿真模型的基础上，编写MATLAB仿真程序来实现两点间的正运动学仿真。通过仿真，可以得出机器人手臂关节运动角位移曲线和机器人手臂末端位移曲线，如图4所示。

从仿真结果可以看出机器人手臂各关节在运动过程中情况正常，运动平稳，连杆之间没有错位冲突的情况，从而也说明了连杆参数设计的合理性和正运动学算法的准确性。

3.3 空间轨迹仿真

假设机器人从A点运动到B点，仿真其运动过程，仿真时间为2 s，采样时间为0.05 s，最终输出各关节的角位移、角速度、角加速度时间曲线如图5所示。

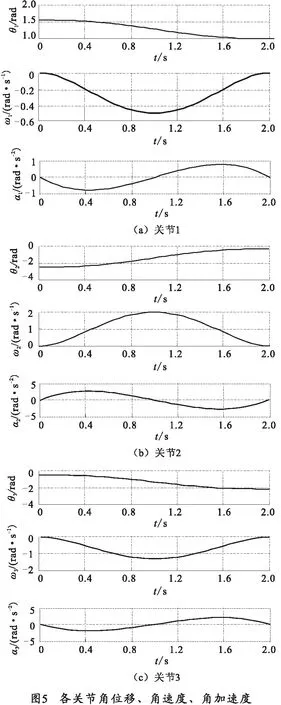
从动态运动中可以看出，机器人各个参数设计合理，连杆和关节都很灵活，可以在工作空间里任意转动。从图5中曲线可以看出，机器人角位移曲线平滑，速度和加速度曲线连续，各连杆没有运动错位，在轨迹规划过程中机器人末端执行器没有产生较大的振动，整个工作过程中运行较为平稳。这些都说明了机械机构的合理性。此外，观察曲线发现机器人在刚刚启动时，关节位移和速度在0.2 s左右才开始发生变化，这是因为驱动器的马达惯性及机械系统摩擦阻尼等因素的影响，在1 s左右达到速度极值，此时瞬时加速度接近零。

3.4 逆运动学仿真

利用RoboticsToolbox中的ikine函数可以实现机器人运动学逆问题的求解。其中ikine函数的调用格式：Q=IKINE(ROBOT,T)编写MATLAB仿真程序来实现从A点到B点两点间的逆运动学仿真。先由正运动学函T=fkine(r,q)可求得A，B点的位姿矩阵。同样可以得出机器人手臂关节运动角位移曲线和机器人手臂末端位移曲线，如图6所示。

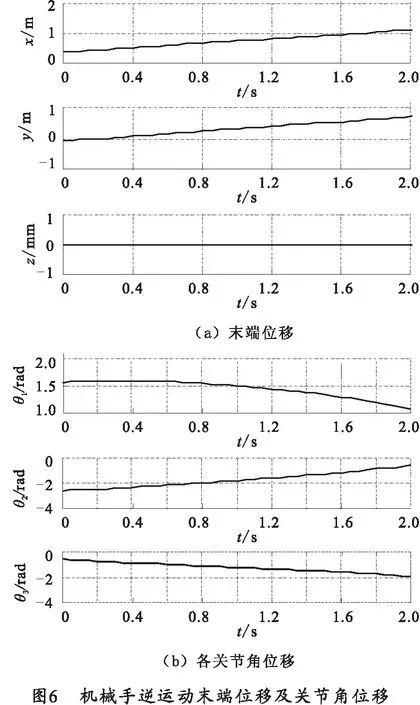
对比图4和图6，可知同是在笛卡尔空间两点间的证运动和逆运动关节角的运动范围虽然相同，但是其运动过程却不尽相同，由于空间两点的位姿是唯一的，所以机器人末端关节的位移变化量对于两种不同的运动情况也是相同的，但其运动中间点的位姿是不同的。通过对笛卡尔空间两点间正运动和逆运动仿真可以看出机器人正逆运动之间的关系，机器人正解是唯一的，而逆解并不唯一。

4 结 论

根据弹药自动装填机械手的工作环境和工作任务，对其进行了结构及参数设计，建立了三维模型、D-H参数、连杆坐标系和运动学方程并分析了它的运动学问题和运动轨迹问题。借助MATLAB对机器人手臂进行建模仿真，仿真结果显示机器人建模与理论的模型一致，运动轨迹与机器人运动学的正解和逆解方程相符，达到了预期的目的。从仿真结果可以看出机器人手臂各关节在运动过程中情况正常，运动平稳，连杆之间没有错位冲突的情况，从而也说明了连杆参数设计的合理性和正运动学算法的准确性。

[1] 徐达,张丽明,张月林.大口径火炮自动装填技术研究[J].火炮发射与控制学报,1996(4):58-62.

XU Da,ZHANG Li-ming,ZHANG Yue-lin.A study on automatic loading techniques for large caliber artillery[J].Journal of Gun Launch& Control, 1996(4): 58-62.(in Chinese)

[2] 马卫军.自行迫击炮自动供输弹机械手的设计及其动力学仿真分析[D].南京:南京理工大学,2004.

MA Wei-jun.Design and dynamic simulation analysis of automatic transfer and loader robotic manipulator for self-propelled mortar system[D].Nanjing:Nanjing University of Science and Technology,2004.(in Chinese)

[3] 孙纯杰.大口径自行火炮弹药自动装填系统方案设计[D].南京:南京理工大学,2005.

SUN Chun-jie.Design of ammunition automatic loading system scheme for large-caliber self-propelled artillery[D].Nanjing:Nanjing University of Science and Technology,2005. (in Chinese)

[4] 侯保林.大口径自行火炮弹药自动装填系统研究[D].南京:南京理工大学,2003.

HOU Bao-lin.Study on ammunition automatic loading system for large-caliber self-propelled artillery[D].Nanjing:Nanjing University of Science and Technology, 2003. (in Chinese)

[5] Willian F Milliken. Autoloading apparatus for large-caliber rapid fire[J].Jane Defence Weekly,2005,2(7):5-27.

[6] 李宗海.中大口径双管火炮自动装填系统方案研究[D].南京:南京理工大学,2009.

LI Zong-hai.Study on automatic loading system scheme of medium and large-caliber double-barreled artillery[D].Nanjing: Nanjing University of Science and Technology,2009. (in Chinese)

[7] 杨杰.供弹机器人的运动学及动力学特性分析[D].哈尔滨:哈尔滨工程大学,2008.

YANG Jie.Analysis of kinematics and dynamics characteristics for shell transfer manipulator[D].Harbin:Harbin Engineering University, 2008. (in Chinese)

[8] 陈恳,杨向东.机器人技术与应用[M].北京:清华大学出版社,2006:35-192.

CHEN Ken, YANG Xiang-dong. Robot technology and application[M].Beijing:Tsinghua University Press, 2006:35-192. (in Chinese)

[9] Srinivasan Alavandar,Nigam M J.Inverse kinematics solution of 3 DOF planar robot using ANFIS[J].Int.J.of Computers, Communications & Control,2008,3:150-155.

[10] 王倩,周一丹,周自强,等.玻璃模具型腔等离子喷焊机器人运动仿真研究[J].制造业自动化,2011,33(5):116-119.

WANG Qian,ZHOU Yi-dan,ZHOU Zi-qiang,et al. Study on the simuIation of glass mould plasma spray welding robot motion[J].Manufacturing Automation, 2011,33(5):116-119. (in Chinese)

[11] 罗家佳,胡国清.基于MATLAB的机器人运动仿真研究[J].厦门大学学报:自然科学版,2005,44(5):640-644.

LUO Jia-jia,HU Guo-qing.Study on the simulation of robot motion based on MATLAB[J]. Journal of Xiamen University:Natural Science, 2005,44(5):640-644. (in Chinese)

[12] 李健,许曼,杨杰.排爆机器人手臂的研制及运动学分析[J].机械与电子,2009(3):66-69.

LI Jian,XU Man,YANG Jie.Design and kinematics analysis of bomb-disposed robot manipulator[J].Machinery & Electronics, 2009(3):66-69. (in Chinese)