自动机缓冲器特性与动强度研究

豆 征, 刘朋科, 李睿远, 李宗贤

(西北机电工程研究所,陕西 咸阳 712099)

每发射一发炮弹,自动机要完成后坐、复进一个工作循环，在自动机停止运动和转变运动方向时,总有一些多余的能量造成机件之间剧烈撞击,尤其以自动机组件后坐到位时的撞击最为强烈.自动机口径越大、射速越高,后坐剩余能量就越多、撞击也就越猛烈,从而造成武器射击精度、零部件寿命降低以及使射手疲劳等一系列不良影响.为了消弱后坐过程的负面影响,在自动武器结构设计中都要涉及到自动机缓冲装置,尤其对中口径自动机更是不可缺少[1-3].文献[4]通过采用湍流模型的计算方法对具有气液组合式的缓冲装置特性进行了仿真分析,并探讨了温度对该缓冲装置的影响.文献[5]采用最佳后坐力控制理论对高射速自动机后坐力进行控制的思路,以某高射速小口径自动机为应用对象,对自动机后坐运动特性进行动态仿真分析.

自动机在连发射击过程中具有较大的后坐能量,这些后坐能量通过缓冲器消耗.如果缓冲器性能参数设计不合理,轻则造成严重冲击,降低射击精度和密集度,重则引发事故.现有自动机缓冲器的研究侧重于对后坐力的影响进行分析,文中从缓冲器优化结构的角度,利用运动分析软件,对各参数的变化与后坐过程的特征参数之间的关系进行分析研究.最终达到优化缓冲器结构、降低后坐冲击、提高射击精度和密集度的目的.

1 缓冲器结构与运动方程

1.1 工作原理

缓冲器结构如图1,缓冲器活塞杆与自动机相连.自动机后坐时,环簧被压缩,后坐能量一部分转化为环簧和气体势能,其余部分被环簧摩擦力、活塞摩擦力及液压阻尼所消耗.环簧和气体势能提供复进能量,复进过程中,能量再次被环簧摩擦力、活塞摩擦力及液压阻尼所消耗,未消耗完的能量再次转化为环簧和气体势能.由于液压阻尼力与自动机的运动速度的平方成正比,因此有效地消耗了后坐能量,降低了后坐力峰值.

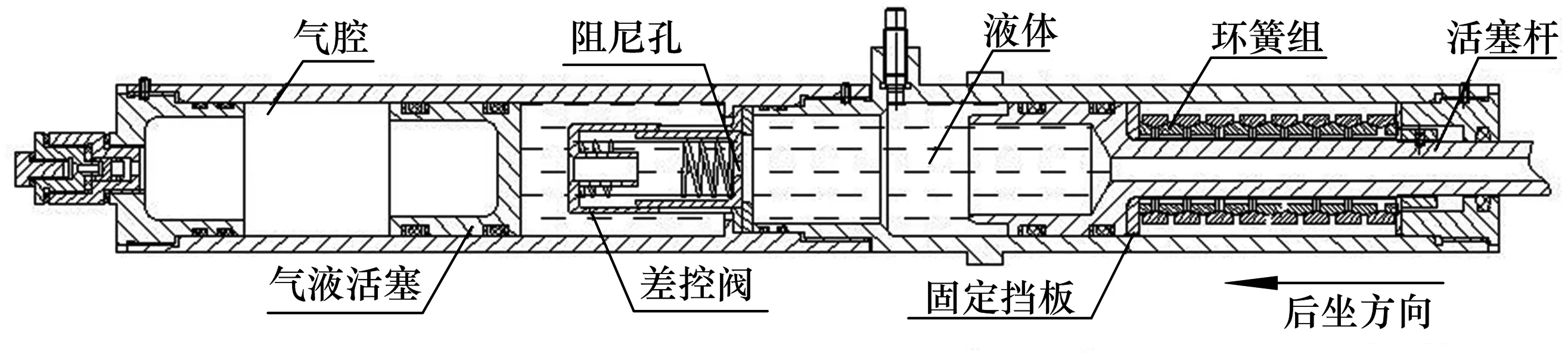
图1 缓冲器结构Fig.1 Buffer structure

1.2 运动方程及初始条件

液体对活塞工作面积所形成的压力,包括储气筒中的气体压力经过液体传递而作用于活塞上那部分压力,克服液体流动阻力而作用于活塞上的压力[6].

缓冲器运动仿真模型如图2.滑轨固定,质量块在滑轨上运动,质量块与滑轨之间有弹簧力和阻尼、摩擦力.弹簧力和阻尼、摩擦力的数值通过弹簧参数和运动副初始条件进行设定.为了使缓冲器运动仿真模型与缓冲器真实情况更为接近,缓冲器的相关参数通过数学计算和试验数据相结合进行分析确定.

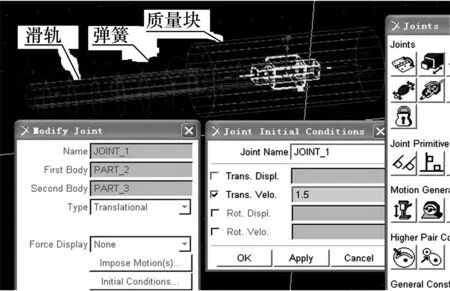
图2 缓冲器运动仿真模型Fig.2 Buffer motion simulation model

自动机后坐阻力方程

R=A1PT+T+mg(fcosθ-sinθ)+F0+kx+

(1)

式中：A1为活塞工作面积，PT为作用于活塞工作面积上的液体压力，T为环簧摩擦簧力和活塞的摩擦力，f为摩擦系数，θ为射角，F0为环簧预压力，k为环簧刚度，x为后坐行程，C为阻尼系数，ρ为液体密度，v为后坐速度，a为漏口面积，τ为气体多变指数,p为气腔内压力,V为气腔容积,A2为气液活塞面积.

在求解自动机运动微分方程时,主要是给出二阶微分方程的迭代格式,设在微小的时间间隔Δt=tn-tn-1内,对自动机运动微分方程逐步积分可得后坐速度与位移的表达式:

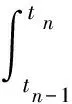
(2)

Xn=Xn-1+Vn-1(tn-tn-1)+

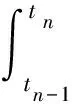
(3)

式中：m为后坐整体质量,Fpt为炮膛合力.

初始条件为自动机射速600发/min,后坐最大距离20 mm,不浮动射击,后坐质量m=0.3×103kg，后坐起始速度v0=0.8 m/s(指弹丸飞出炮口时自动机的最大后坐速度)，总刚度k=3×105N/m,阻尼系数C=3 000,预压力Fy=1.4×104N/m.

2 仿真结果分析

运用ADAMS软件对缓冲器后坐过程进行运动仿真,通过改变参数设置,得到缓冲器运动关系曲线.ADAMS软件使用交互式图形环境和零件库、约束库、力库,创建完全参数化的机械系统几何模型,对虚拟机械系统进行静力学、运动学和动力学分析,输出位移、速度、加速度和反作用力曲线.

2.1 刚度的变化对加速度的影响

在其他条件不变的情况,改变缓冲器刚度数值,加速度的变化如图3.从图中可看出,刚度减小,加速度曲线周期延长,幅值减小,走势更加平缓,这使振动变得柔和,即冲击特性好.在0.26～0.5 s之间,加速度变化率发生明显变化,这表明此刻有剧烈冲击,其原因有,一是此时正是静摩擦力刚转变成动摩擦力;二是阻尼孔处由于液体由静到动的转变,发生动力效应[7-8],导致液体压力发生变化,液体压力的变化与摩擦力变化联合作用影响加速度的变化,刚度越大,这种影响越显著，这说明减小刚度对降低冲击是有利的.另一方面,刚度的减小,在吸收同样后坐能量的情况下,会有较大的后坐距离.因此,在对冲击振动较为敏感的情况下,比如航炮,可以延长后坐距离,为缓冲吸振提供充裕的空间,减弱冲击.

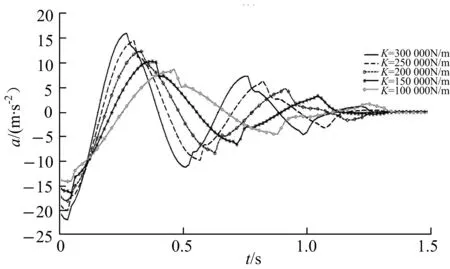
图3 刚度与加速度的关系Fig.3 Relation of stiffness and acceleration

2.2 阻尼对加速度的影响

阴尼对加速度的影响如图4，图中可看出,随着阻尼的增大,加速度曲线变得平缓，阻尼达到一定数值,加速度曲线快速趋近0,这说明,阻尼对能量的快速消耗使自动机后坐的振荡时间缩小.加速度从峰值变化到0的初始段出现的剧烈波动随着阻尼的增大逐渐缓和,这说明在从静摩擦转化为动摩擦的时间段,阻尼可以有效抑制冲击.另一方面,阻尼消耗的能量会使缓冲器温升加剧,密封效果受到破坏,可靠性下降.所以,阻尼的大小既要满足规定行程内缓冲吸振的要求,又不能使缓冲器温升太快,破坏可靠性.从图4还可看出,在加速度从0变化到峰值时,曲线导数变化率较大,而从峰值回到0的过程曲线缓和;阻尼越大,这种趋势越明显,而加速度为0时,正是速度最大时,即冲量最大,这说明冲量越小,阻尼对加速度的影响越显著.

图4 阻尼与加速度的关系Fig.4 Relation of damp and acceleration

2.3 环簧预压力对加速度的影响

环簧预压力对加速度的影响如图5，图中可看出,预压力的增大使加速度曲线幅值增大,周期不变，较小的预压力使加速度曲线快速趋于0,这说明预压力越小,环簧储存的能量越少,能量越少,环簧所起的作用越小,这种情况下,后坐能量主要被液压阻尼所消耗.由于复进过程需要环簧提供能量克服阻尼与摩擦力,所以环簧后坐过程中必需储存足够的能量用于复进.从图5还可看出,无论预压力怎样变化,到达同一加速度的时间点是一致的,这说明,阻尼不改变加速度的变化周期,但改变了加速度相同时间点对0点的偏移值.预压力越大,后坐振荡过程越长,后坐阻力越大;较小的预压力会降低冲击.在满足使用要求的前提下,为了减小振荡,应尽量降低预压力.

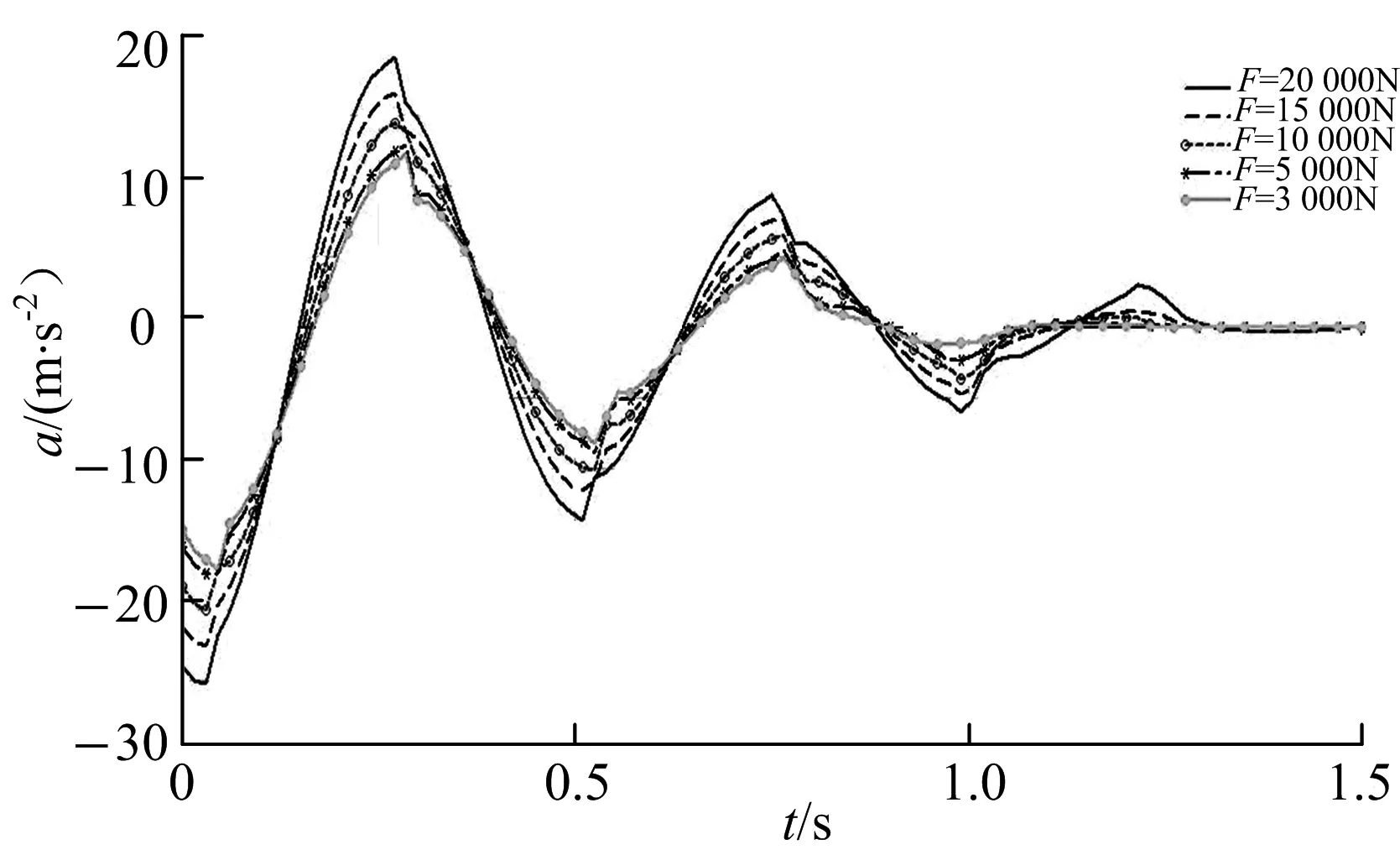
图5 预压力与加速度的关系Fig.5 Relation of preload and acceleration

2.4 不同后坐起始速度与摩擦力的关系

不同后坐起始速度与摩擦力关系如图6，图中可看出,对于不同的后坐起始速度,动摩擦力是一样的,但在不同周期,静摩擦力表现不同.在缓冲器由静到动的过程中,摩擦力经过短时间的振荡过程后趋于平稳.对不同后坐起始速度来说,摩擦力发生剧烈波动的时刻不完全相同.文中，在0～50 ms内,起始速度较低时摩擦力曲线振荡较为剧烈;在50～100 ms内,5种不同初速的摩擦力全部发生剧烈振荡;100～130 ms之间,各摩擦力曲线变化差异很大;130 ms之后,低起始速度的摩擦力趋于平稳,最高起始速度的摩擦力曲线发生两次振荡.总的说来,在整个后坐过程中,后坐起始速度较低时的静摩擦力表现最为活跃.较高的静摩擦力水平是造成振动与冲击的主要成因.

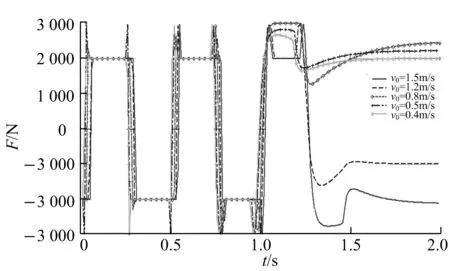
图6 后坐起始速度与摩擦力的关系Fig.6 Relation of recoil initial velocity and frictional force

2.5 多参数影响分析

阻尼系数(δ)与刚度(k)对后坐速度(v)的影响如图7(负值区域的曲面是为了分析后坐速度边界变化趋势),随着刚度和阻尼的增大,后坐速度减小,当刚度趋于0或者阻尼趋于最小时,后坐速度达到极大值,也就是说后坐部分的动能几乎没有转化或消耗;后坐阻力(F)与后坐速度(v)和阻尼系数(δ)的关系如图8(负值区域的曲面是为了分析后坐阻力边界变化趋势),阻尼系数与后坐阻力呈线性递增关系,后坐速度与后坐阻力呈抛物线递增关系,也就是说后坐动能越大,后坐阻力(可理解为后坐质量部分的反作用力)的增量越大,这对射击精度和射击平台的安全性是不利的;根据动量守恒定理,通过适当延长后坐行程,增加作用力时间,可降低对射击平台的作用力.在缓冲器设计上体现为降低刚度,增大阻尼和摩擦力.

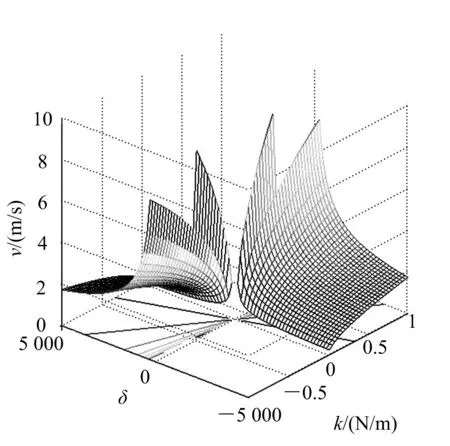
图7 后坐速度变化曲面Fig.7 Recoil velocity variations surfaces figure

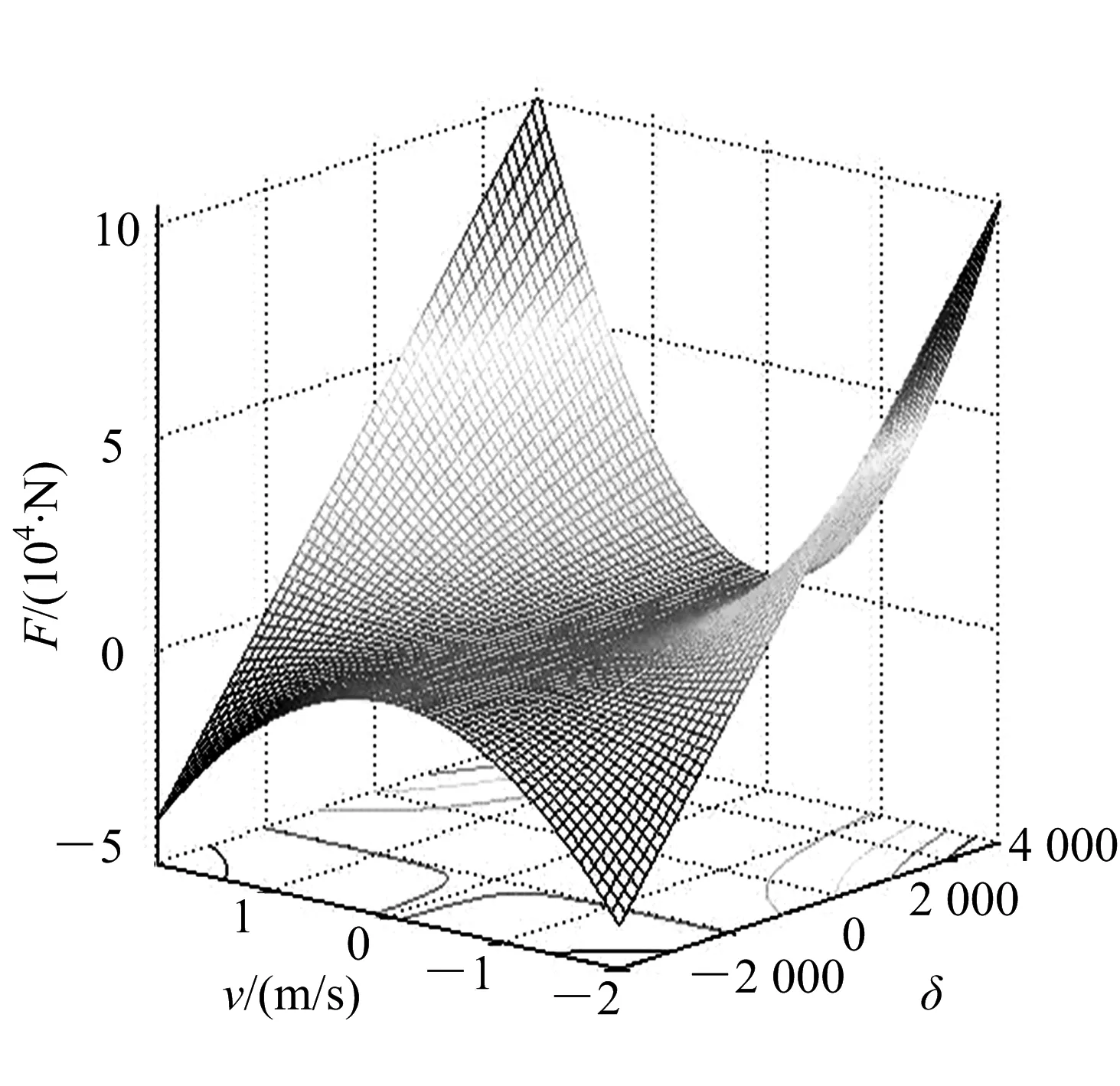
图8 后坐阻力变化曲面Fig.8 Recoil resistance variations surfaces figure

3 缓冲器动强度有限元分析

动强度表征物体抵抗共振所致形变的能力.通过研究缓冲器的共振形变(即模态)来考察其动强度的不足.有限元法的基本思路是将弹性体离散为有限多个单元,即所谓的网格划分,而后根据各个单元节点的位移协调条件和平衡条件建立振动微分方程.由于模态是系统结构的固有特性,与外载无关,所以在进行模态分析时,不需要设置外载边界条件,即总载荷向量{f(t)}=0.由于阻尼对结构的固有频率和振型影响很小,所以,不考虑系统阻尼影响.因此,无阻尼多自由度系统的自由振动微分方程为

(4)

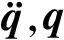
式(4)对应的特征值方程为:

(K-w2M)q=0

(5)

式中:w为系统的固有频率.

求解特征值方程式(5)就可以得到w和q,即系统的固有频率和主振型[9-11].

根据自动机实际射速范围,取前10阶模态进行研究.缓冲器左端施加约束,对缓冲器进行有限元动强度分析,各阶振型及频率如图9.

从图中可以看出,第3，4，6，7，9，10阶共振频率使活塞杆受到弯曲应力,这会使活塞摩擦力增大;第5阶共振频率使差控阀的内外环配合面出现锥形分布的应力谱,由于差控阀径向外泄量增大,液压阻尼的作用被消弱;第1，2阶共振频率使缓冲器受到整体弯曲应力,由于左端的约束,缓冲器外筒在应力作用下发生形变,气液活塞的运动阻力增大,从而消弱液压阻尼的耗能作用.由于缓冲器的受力情况可以视同二力杆,任何纵向弯曲形变都会使两端的力不同线,这就加剧了缓冲器的弯曲倾向.通过调整射速,可以规避以上共振频率;在射速确定时,也可以改进缓冲器结构使缓冲器与射击频率不发生共振.另外,图中还可看出,第3，6，7，9，10阶振型对抗弯动强度有更高的要求,在此共振频率下工作,需要对缓冲器进行动强度增强设计.

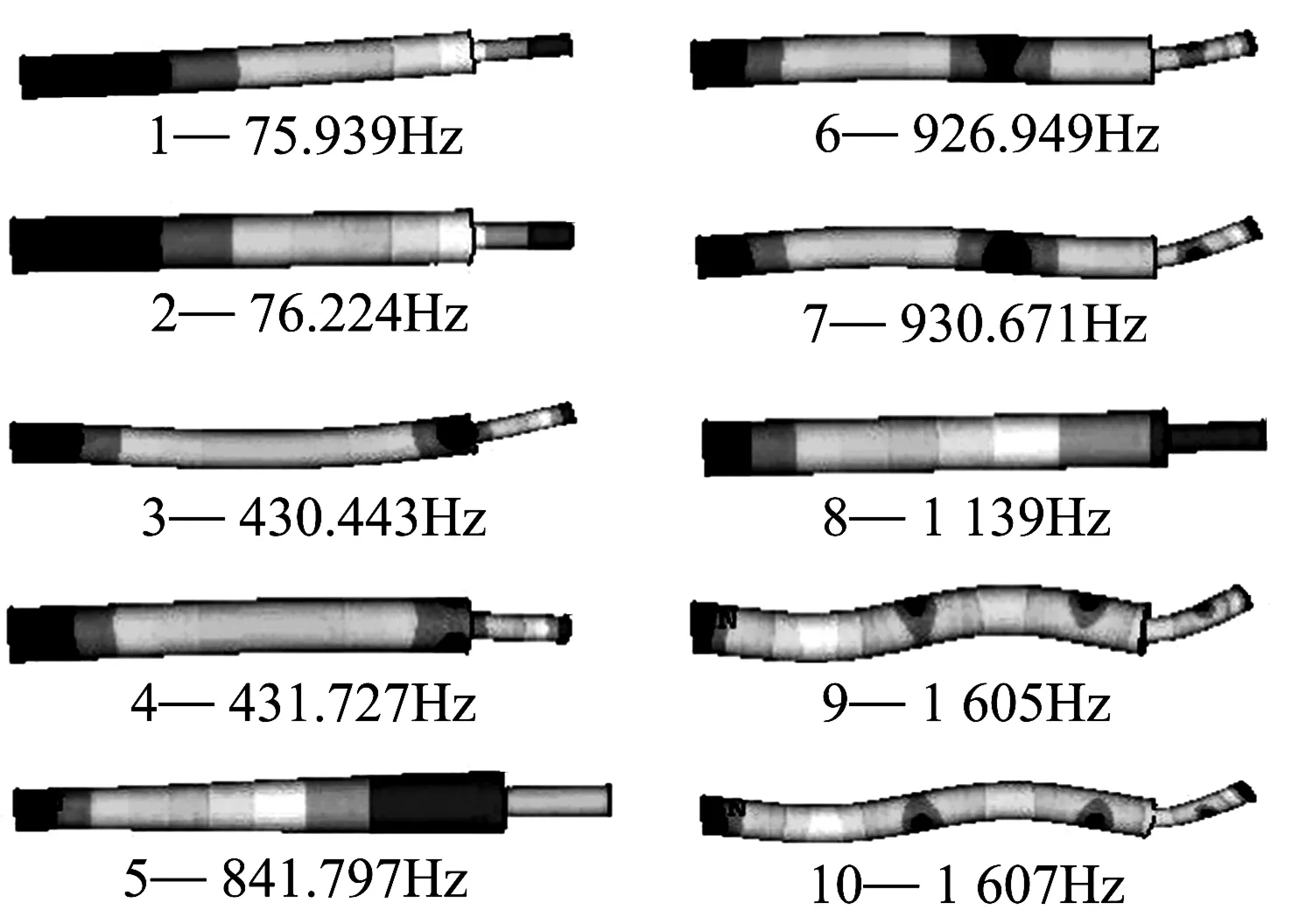
图9 各阶振型与频率Fig.9 Type and freqnency of each vibration

4 结论

1)阻尼系数每增加1%,加速度下降0.55%;刚度每下降1%,加速度降低0.96%,加速度变化率越大,冲击越大,这就是说通过提高阻尼系数比降低刚度更能缓和冲击,且不需要延长后坐行程.

2)较大的后坐起始速度使后坐部分具有较高的动能,这些动能部分转化成势能,势能越大,静摩擦力作用时间越短,引起的振动冲击越弱,在结构设计中可以使后坐过程的初始段具有较高的阻尼,阻尼在消耗能量的同时还可以吸收振动;后坐过程的末段要具有较好的弹簧可回复性,以利于缓冲器克服摩擦力和阻尼复进到位.

3)在共振频率附近工作,结构刚度不足会破坏缓冲器初始条件,进而恶化缓冲器性能.提高缓冲器结构动强度可以改善中低频振动稳定性,防止缓冲器因为过大形变丧失对后坐能量的吸收.

[1] 赵少华. 转管机枪缓冲器优化设计 [D].山西太原：中北大学,2010：4.

[2] 丁文波,赵俊利,赵凡, 基于MATLAB的曲线后坐缓冲器的仿真与研究[J]. 机械工程与自动化,2011, (2):79-82.

Ding Wenbo,Zhao Junli,Zhao Fan. Simulation study based on the the MATLAB curve of recoil buffer[J].MechanicalEngineeringandAutomation,2011 (2):79-82.(in Chinese)

[3] 刘佳,刘树华. 影响缓冲器性能的变参数分析[J]. 机械工程与自动化,2012(2):6-9.

Liu Jia, Liu Shuhua. Analysis on varying parameters affecting buffer performance[J].MechanicalEngineeringandAutomation,2012 (2):6-9.(in Chinese)

[4] 戴劲松,刘 振,王茂森,等. 高频冲击作用下高阻尼气液缓冲装置动态仿真[J].火炮发射与控制学报,1998(2):22-25.

Dai Jingsong, Liu Zhen, Wang Maosen, et al. Buffer device dynamic simulation of high-frequency shock effect of high damping gas-liquid [J].GunLaunch&Control,1998(2):22-25.(in Chinese)

[5] 戴劲松,王茂森,苏晓鹏.高射速自动机后坐力控制[J].火炮发射与控制学报, 2011(2):1-3.

Dai Jingsong, Wang Maosen, Su Xiaopeng. High rate of fire automatic machine recoil control[J].GunLaunch&Control, 2011(2):1-3.(in Chinese)

[6] 高树滋,陈运生.火炮反后坐装置设计[M].北京:兵器工业出版社,1994：5-17.

[7] 戴成勋,靳天佑,朵英贤.自动武器设计新编[M]. 北京:国防工业出版社,1990：28-30.

[8] Harrison A M, Edge K A. Reduction of axial pistonpump pressure ripple[J].ProceedingsInstitutionofMe-chanicalEngineers, 2000, 214(1): 53-63.

[9] Curadelli O,Ambrosini D,Mirasso A,et al.Resonant frequencies in an elevated spherical container partially filled with water:FEM and measurement[J].JournalofFluidsandStructures,2010,26:148-159.

[10] Ventsel E S,Naumenko V,Strelnikova E,et al.Free vi-brations of shells of revolution filled with a fluid[J].EngineeringAnalysiswithBoundaryElements,2010,34: 856-862.

[11] Xia Y,Ni Y Q,Ko J M,et al.ANCRiSST benchmark problem on structural health monitoring of high-rise slender structures-phase I:field vibration measurement[C]//Proceedingsofthe5thInternationalWorkshoponAdvancedSmartMaterialsandSmartStructuresTechnologies.Boston,USA:[s.n.],2009:30-31.