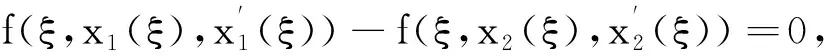无穷区间上二阶m点共振边值问题解的存在性和唯一性
禹长龙,李志广,魏会贤,王菊芳
(1.河北科技大学理学院,河北石家庄 050018;2.山西大同大学数学与计算机科学学院,山西大同 037009;3.石家庄铁路职业技术学院基础部,河北石家庄 050047)
无穷区间上的二阶微分方程边值问题起源于对非线性椭圆方程径向对称解和半无穷多孔介质气压模型的研究,并且已经取得了许多研究成果[1-12]。
1970年,LANDESMAN等研究了半线性椭圆方程边值共振问题解的存在性[13]。此后的几十年间,对于非线性微分方程共振边值问题的研究获得了大量的重要结果,特别是在共振情形下,对于非线性常微分方程2点边值问题(Dirichlet问题、Neumann问题、周期边值问题)的研究中,获得的结果更是系统[14-22]。然而,无穷区间上二阶多点共振边值问题的研究成果尚少。
在文献[15]中,LIAN等利用迭合度理论研究了无穷区间上的二阶3点共振边值问题
和
的可解性和解的唯一性,其中f:[0,+∞)×R2→R,e:[0,+∞)→R是连续的,且η∈(0,+∞)。
受文献[15]的启发,笔者研究无穷区间上的二阶m点共振边值问题:
(1)
和
(2)
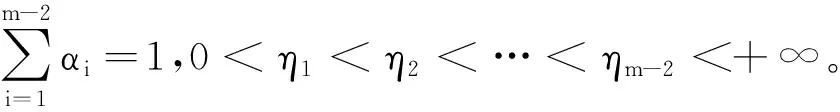
1 预备知识
定义1f:[0,+∞)×R2→R称为S-Carathéodory函数,当且仅当

1)Lx≠λNx对于∀(x,λ)∈[(domLKerL)∩∂Ω]×(0,1)成立;
2)Nx∉ImL对于∀x∈KerL∩∂Ω成立;
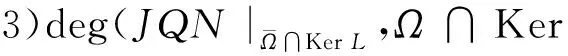
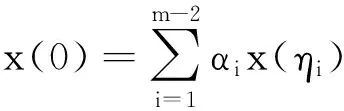

注1由引理1可知半无穷区间上的二阶m点边值问题(1)和边值问题(2)就等价为文献[15]中研究的边值问题,且η∈[η1,ηm-2]。
定义空间X,Y为
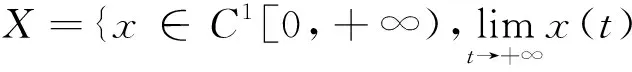
(3)

(4)
定义线性算子L:domL⊂X→Y为

(5)
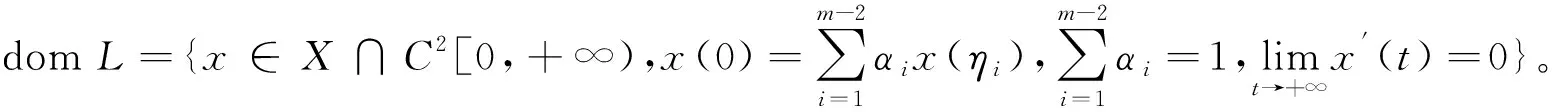

这里
记ω(t)=e-t/(1-e-ηm-2)并定义连续映射Q:Y→Y,即

(6)


定义连续映射P:X→KerL为
(Px)(t)=x(0),t∈[0,+∞),
(7)
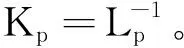
定义非线性算子N:X→Y为
(Nx)(t)=f(t,x(t),x′(t)),t∈[0,+∞),
(8)
那么,边值问题(1)就等价于
x=Px+Kp(I-Q)Nx,
(9)
JQNx=0,
(10)
其中,J:ImQ→KerL是一个同构。
为了应用定理1,需证明N是L-紧的,即要证明算子QN和Kp(I-Q)N都是全连续的。因为Arzelà-Ascoli定理对非紧区间的情形不适用,笔者将用下面的判定准则。
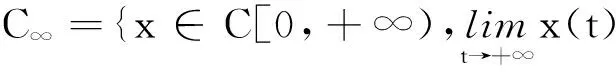
a)M中的所有函数是一致有界的;
b)M中的所有函数在[0,+∞)的任意紧区间都是等度连续的;
引理2设f是一个S-Carathéodory函数,则N是L-紧的。
证明显然,QN和Kp(I-Q)N是连续的,只需要证明紧性,即QN和Kp(I-Q)N从有界集映射到一个相对紧集。

‖QNx‖Y=max{‖QNx‖∞,‖QNx‖L1,‖QNx‖1}≤‖φr‖1·‖ω‖Y<+∞,
注意到ImQ≃R,于是QN是紧的。
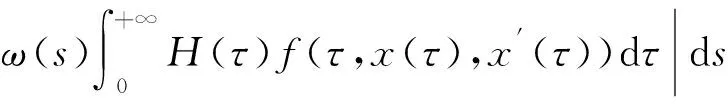
|(KP,Qx)(t1)-(KP,Qx)(t2)|≤

本期每笔已投放天数,为贷款的合同履行期限与考核期的交集。往年放款的计算起始日为本年1月1日,考核期内放款的计算起始日为放款日;考核期内到期的贷款计算截止日为贷款结清日,考核期内未到期的贷款计算截止日为考核期截止日。
和
|(KP,Qx)′(t1)-(KP,Qx)′(t2)|≤
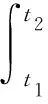
成立,则KP,QU是等度连续的。由定理2可知若KP,QU和(KP,Q)′U在无穷大处是等度收敛的,则KP,QU在X中是相对紧的。事实上,当t→+∞时,
|(KP,Qx)(t)-(KP,Qx)(+∞)|≤

和
|(KP,Qx)′(t)-(KP,Qx)′(+∞)|≤
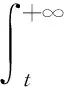
是一致成立的。证毕。
2 主要结论
2.1 边值问题(1)解的存在性定理
定理3设f:[0,+∞)×R2→R是S-Carathéodory函数。假定
H1)存在非负函数p,q,r∈L1[0,+∞)满足:

当t∈[0,+∞)时,对所有的(u,v)∈R2,|f(t,u,v)|≤p(t)|u|+q(t)|v|+r(t)几乎处处成立;
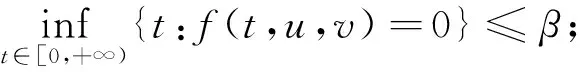
H3)存在B1,l>0,m,n≥0使得对所有的u∈R,|u|>B1,∀t∈[0,β],v∈R有|f(t,u,v)|≥l|u|-m|v|-n成立;
H4)存在B2>0使得对所有的u∈R,|u|>B2,要么对t∈[0,+∞),uf(t,u,0)≤0几乎处处成立,要么对t∈[0,+∞),uf(t,u,0)≥0几乎处处成立,则边值问题(1)至少有1个解,若
证明设X,Y,L,N,P,Q是式(3)-式(8)中定义的。下面分步来证明。
步骤1 设Ω1={x∈domLKerL:Lx=λNx,∃λ∈[0,1]},则Ω1是有界的。
易证对λ∈[0,1],函数x满足Lx=λNx当且仅当x是
x=Px+λKp(I-Q)Nx,
(11)
JQNx=0
(12)


于是有
又

即有
因此,‖x‖X≤max{M1,M2}:=M,故Ω1是有界的。
步骤2 设Ω2={x∈KerL,Nx∈ImL},则Ω2是有界的。

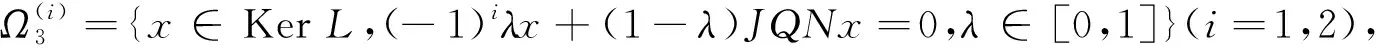
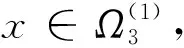
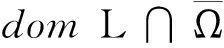

1)对于∀(x,λ)∈[(domLKerL)∩∂Ω]×(0,1),有Lx≠λNx;
2)对于∀x∈KerL∩∂Ω,有Nx∉ImL。
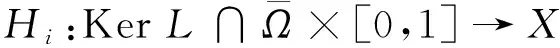
2.2 边值问题(2)解的存在性定理
因为积分中值定理对于半无穷区间的情形无效,所以文献[12]—文献[14]中对于扰动系统在有限区间上所用的方法并不适用。于是笔者将运用由边值问题(1)得到的结论来建立关于边值问题(2)解的存在性结论。


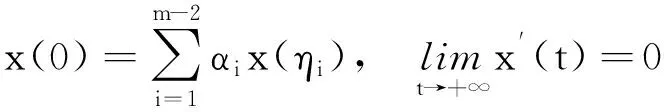
至少有1个解。选定其中一个解并表示成

(13)
令x(t)=z(t)+E(t),则
z″(t)=f(t,z(t)+E(t),z′(t)+E′(t)), 0 (14) (15) 下面证明边值问题(14)与边值问题(15)至少有1个解。设X,Y,L,P,Q是定理3中所定义的,且定义算子N1:X→Y为(N1z)(t)=f(t,z(t)+E(t),z′(t)+E′(t)),t∈[0,+∞),则边值问题(14)与边值问题(15)等价于:z=Pz+Kp(I-Q)N1z,JQN1z=0。 推论1设Ω4={z∈domLKerL,Lz=λN1z,∃λ∈[0,1]},Ω5={z∈KerL,N1z∈ImL},则Ω4和Ω5是有界的。 所以,‖z‖X≤max{M3,M4}且Ω4是有界的。 则 对f加强条件,可以得出前面研究边值问题解的唯一性定理。 定理5设f是一个S-Carathéodory函数,且定理3中的条件H2)和条件H4)成立,同时满足: H7)存在β1>0使得对所有的ui,vi∈R(i=1,2),如果f(t,u1,v1)-f(t,u2,v2)有零点,则有 H8)存在l>0,m≥0使得对所有的t∈[0,max{β,β1}]和(u1,v1),(u2,v2)∈R2有 |f(t,u1,v1)-f(t,u2,v2)|≥l|u1-u2|-m|v1-v2|, 那么,当max{α,α1}<1时,边值问题(1)有唯一解,其中α是定理1中所定义的,且 证明设X,Y,L,Z,P,Q是定理3中所定义的。因为f是一个S-Carathéodory函数,所以,r(t)=|f(t,0,0)|∈Y。由定理3知边值问题(1)至少有1个解。 假设边值问题(1)有2个解x1,x2∈X,令x=x1-x2,则x满足 (16) (17) (18) 因此, 因为并不交错,但‖x‖∞=0,所以x1=x2。则边值问题(1)有唯一的解,证毕。 同样的,可以得边值问题(2)的唯一性结论。 参考文献/References: [1] AGARWAL R P, O’REGAN D. Infinite Interval Problems for Differential,Difference and Integal Equations[M]. Netherlands:Kluwer Academic Publisher, 2001. [2] AGARWAL R P, O’REGAN D. Nonlinear boundary value problems on the semi-infinite interval: An upper and lower solution approach[J]. Mathematika,2002,49:129-140. [3] 索秀云,郭少聪,张素芬,等.二阶脉冲微分方程m点边值问题的正解[J].河北科技大学学报,2011,32(6):519-523. SUO Xiuyun,GUO Shaocong,ZHANG Sufen,et al.Positive solutions tom-point boundary value problems of second order impulsive differential equations[J].Journal of Hebei University of Science and Technology,2011,32(6):519-523. [4] BAXLEY J V. Existence and uniqueness for nonlinear boundary value problems on infinite interval[J]. J Math Anal Appl,1990,147:127-133. [5] JIANG D, AGARWAL R P. A uniqueness and existence theorem for a singular third-order boundary value problemon [0, +∞)[J]. Appl Math Lett,2002,15:445-451. [6] 董士杰.非线性离散周期边值问题的可解性[J].河北科技大学学报,2012,33(5):381-383. DONG Shijie.Sowability for nonliner discrete periodic boundary value problems[J].Journal of Hebei University of Science and Technology,2012,33(5):381-383. [7] MA R. Existence of positive solution for second-order boundary value problems on infinite intervals[J]. Appl Math Lett,2003,16:33-39. [8] LIAN H, GE W. Solvability for second-order three-point boundary value problems on a half-line[J]. Appl Math Lett, 2006, 19(10) :1 000-1 006. [9] 杨 飞,刘玉敬,郭彦平.含有一阶导数的非局部四阶边值问题正解的存在性[J].河北科技大学学报,2013,33(4):283-289. YANG Fei,LIU Yujing,GUO Yanping.Positive solutions to nonlocal fourth-order boandary value probleons with dependence on the first order derivative[J].Journal of Hebei University of Science and Technology,2012,33(4):283-289. [10] LIAN H, PANG H, GE W. Triple positive solutions for boundary value problems on infinite intervals[J]. Nonlinear Analysis, 2007,67:2 199-2 207. [11] GUO Yanping, YU Changlong, WANG Jufang. Existence of three positive solutions form-point boundary value problems on infinite intervals[J]. Nonlinear Analysis, 2009,71:717-722. [12] YU Changlong, GUO Yanping, JI Yude. Existence of solutions form-point boundary value problems on a half-line[J]. Advances in Difference Equations,2009,60:914-916. [13] LANDESMAN E M, LAZER A C. Nonlinear perturbations of linear elliptic boundary value problems at resonance[J]. J Math Mech, 1970, 19(7): 609-623. [14] 索秀云,郭少聪,张继叶,等.四阶非局部边值问题方程组正解的存在性[J].河北科技大学学报,2012,33(3):197-201. SUO Xiuyun, GUO Shaocong,ZHANG Jiye, et al.Existence of positive solutions for nonloeal forth order boundary value problem systems[J].Journal of Hebei University of Science and Technology,2012,33(3):197-201. [15] GUPTA C P. Solvability of multi-point boundary value problems at resonance[J]. Results Math, 1995,28:270-276. [16] FENG W, WEBB J R L. Solvability of three-point boundary value problems at resonance[J]. Nonlinear Anal, 1997,30:3 227-3 238. [17] 刘玉敬,郭少聪,郭彦平.带有积分边值条件的三阶边值问题正解的存在性[J].河北科技大学学报,2012,33(2):93-96. LIU Yujing, GUO Shaocong,GUO Yanping.Existence of positive solutions of the third order boandary value problems with integral boundary conditions[J].Journal of Hebei University of Science and Technology,2012,33(2):93-96. [18] LIU B. Solvability of multi-point boundary value problem at resonance (Ⅱ)[J]. Appl Math Comput, 2003,136:353-337. [19] LIAN H, PANG H, GE W. Solvability for second-order three-point boundary value problems at resonance on a half-line[J]. J Math Anal Appl, 2008,337:1 171-1 181. [20] LIU B. Solvability of multi-point boundary value problem at resonance (Ⅲ)[J]. Appl Math Comput, 2002,129:119-143. [21] 江卫华,陈志红.奇异(k,n-k)共轭多点边值问题方程组的正解[J].河北科技大学学报,2011,32(4):303-307. JIANG Weihua,CHEN Zhihong.Positive solutions to system of singular(k,n-k)conjugate multi-point boundary value problems[J].Journal of Hebei University of Science and Technology,2011,32(4):303-307. [22] MAWHIN J. Topological degree and bondary value problems for nonlinear differential equations in topological methods for ordinary differential equations[A]. Lecture Notes in Math[C].[S.l.]: Springer-Verlag, 1991.74-142.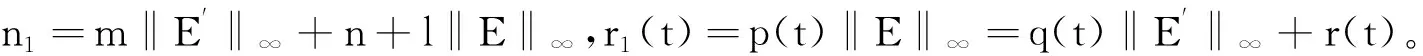

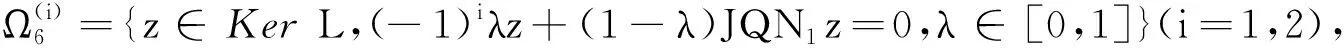

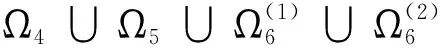
2.3 唯一性定理