用MATLAB程序预测地平类药物的熔点

李志伟，郭海谦，吴 芬

(1.河北科技大学化学与制药工程学院，河北石家庄 050018；2.石药集团欧意药业有限公司，河北石家庄 050051)

药物的性质很大程度上取决于药物分子的结构，通过分析药物分子的结构，可以发现药物的性质和结构之间存在的某种定量关系[1]。许多因素都影响药物的各种理化性质，如在化合物分子中分子的电荷分布及立体因素、官能团的位置等。许多学者也用人工神经网络或回归方程等方法对各种药物进行研究[2-14]。

1 参数及模型

根据文献[4]中的方法对地平类药物构建相似的分子参数N和T，与该药物的熔点进行关联，构建预测的数学模型，得到地平类药物的熔点计算值。普拉地平分子结构见图1。

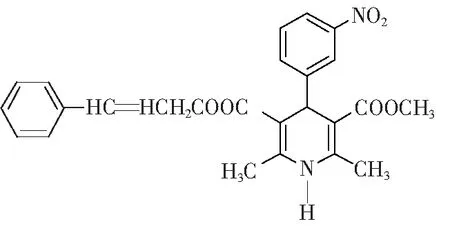
图1 普拉地平分子结构Fig.1 Molecular structure of pranidipine

例如：对普拉地平的分子参数N，T进行计算：

T=(δ0)-0.5× 6+(δNH)-0.5+(δN)-0.5+(δC)-0.5×9+(δCH)-0.5×12+(δCH2)-0.5+(δCH3)-0.5×3=1.808×6+0.280 +1.191+0.5×9+0.577×12+0.707+1×3=27.449，

N=0.2+1/3=0.533。

依照上述计算方法，将地平类药物的熔点、分子参数N和T值列入表1。

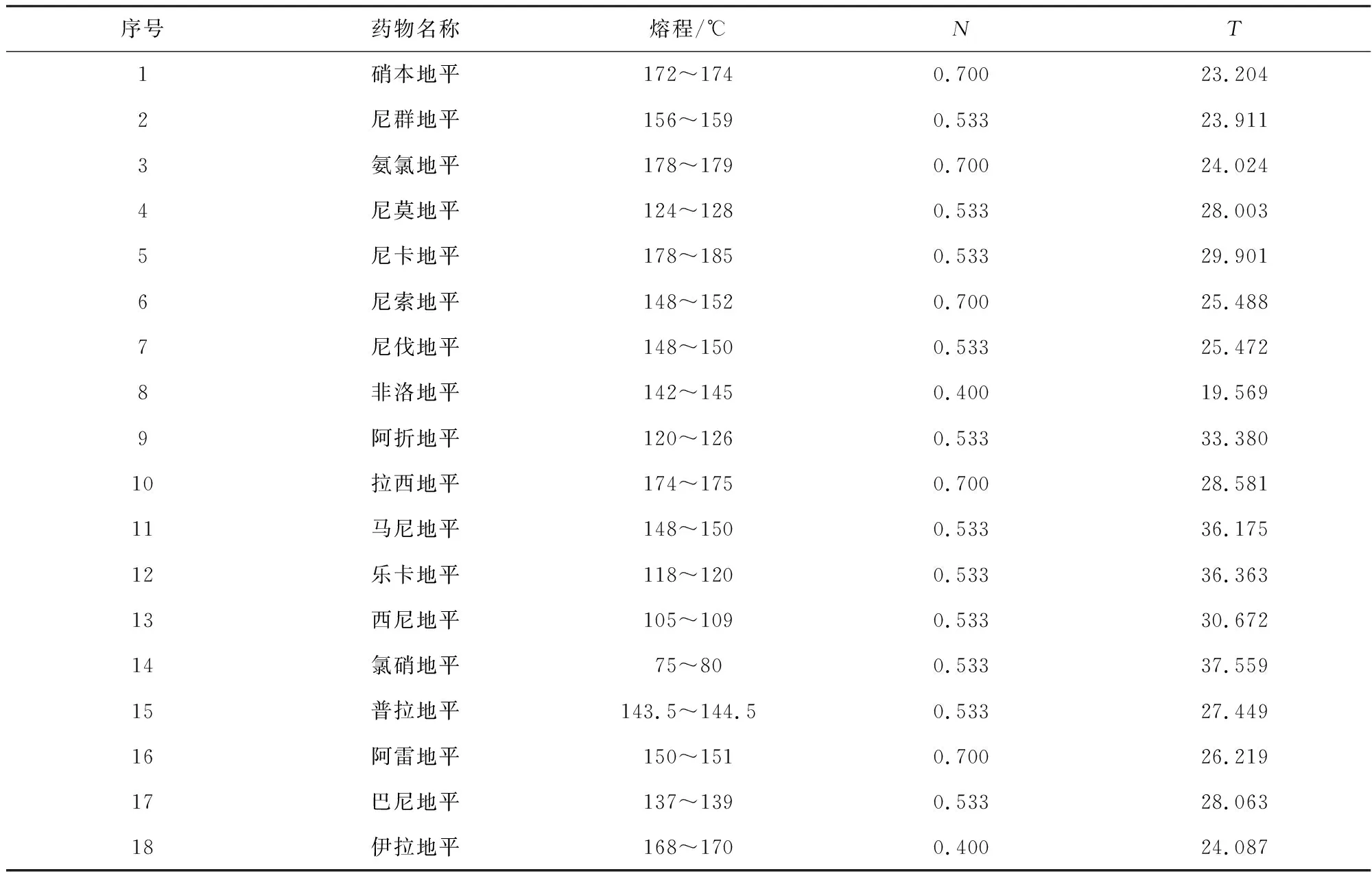
表1 地平类药物熔点实验值与分子参数N，T

2 编制程序

2.1 回归方程程序

mmin=[172 156 178 124 178 148 148 142 120 174 148 118 105 75]；

mmax=[174 159 179 128 185 152 150 145 126 175 150 120 109 80]；

format bank；

mpm=(mmin+mmax)/2%程序所用熔点均为熔程平均值

n=[0.7 0.533 0.7 0.533 0.533 0.7 0.533 0.4 0.533 0.7 0.533 0.533 0.533 0.533]′；

t=[23.204 23.911 24.024 28.003 29.901 25.488 25.472 19.569 33.380 28.581 36.175 36.363 30.672 37.559]′；

y=[mpm]′；

x=[ones(14,1) n t]; %对数据拟合新的方程，同时和文献中方程作图对比;

[b,bint,r,rint,stats]=regress(y,x);

figure；

rcoplot(r,rint)；

pre_mp=～6.393 1*t+107.425 78*n+260.080 9；

mp=b(3)*t+b(2)*n+b(1);

no=1:14；

figure；

plot(no,mmin,'ro',no,pre_mp,'*',no,mmax,'ro')；

figure；

plot(no,mmin,'ro',no,mp,'*',no,mmax,'ro')；

[t1,n1]=meshgrid(18:2:38,0.8:～0.1:0.3)；

mp3=～6.393 1*t1+107.425 78*n1+260.080 9；

mp4=b(3)*t1+b(2)*n1+b(1)；

figure；

set(gcf,'defaultlinelinewidth',1.5)；

plot3(t,n,pre_mp,'～y*'),hold on,surf(t1,n1,mp3),shading interp,hold on，…

plot3(t,n,mp,'～～m'),hold on,surf(t1,n1,mp4),shading interp，…

hold on,plot3(t,n,mmin,'o'),hold on,plot3(t,n,mmax,'v'),xlabel('T'),ylabel('N')，…

zlabel('melting point'),title('Surfaces Before and after the Curve Fitting')；

choose=input('Do you want to test 4 groups of data,input "1" to go on or"0" to stop.')；

if (choose==0),break；

else

n15=input('test 15th N: ')；

t15=input('test 15th T: ')；

Test_mp15=b(3)*t15+b(2)*n15+b(1)

Pre_mp15=～6.393 1*t15+107.425 78*n15+260.080 9

余下3个药物验证程序略去。

2.2 神经网络程序

数据输入部分略。

P(2,:)=(p(2,:)～min(p(2,:)))/(max(p(2,:))～min(p(2,:))); % p为参数T，N组成的矩阵

T=(t～min(t))/(max(t)～min(t)); % t为熔程平均值

rand('state',0)；

%net=newff(minmax(P),[6,1],{'tansig','purelin'},'trainlm')；

net=newff(minmax(P),[9,1],{'tansig','purelin'},'traingdx')；

%以上两行可交替注释屏蔽训练

net=init(net)

net.trainParam.epochs = 10 000；

net.trainParam.goal = 0.01；

[net,tr]=train(net,P,T)；

mmin=[172 156 178 124 178 148 148 142 120 174 148 118 105 75]；

mmax=[174 159 179 128 185 152 150 145 126 175 150 120 109 80]；

format bank；

mp=sim(net,P).*(max(t)～min(t))+min(t)

no=1:14；

figure；

plot(no,mmin,'ro',no,mp,'*',no,mmax,'ro')；

choose=input('Do you want to test 4 groups of data,input "1" to go on or"0" to stop.')；

if (choose==0),break；

else

N15=input('test 15th N: ')；

t15=input('test 15th T: ')；

T15=(t15～min(p(2,:)))/(max(p(2,:))～min(p(2,:)))；

Test_mp=sim(net,[N15 T15]').*(max(t)～min(t))+min(t)

余下3个药物验证程序略去。

3 运行结果

3.1 回归方程程序运行结果

程序拟合所得方程为

Test_mp= ～ 2.85T+128.79N+151.85。

(1)

文献[4]中方程为

Pre_mp= ～6.39T+107.43N+260.08。

(2)

回归方程法熔点计算值及误差见表2。

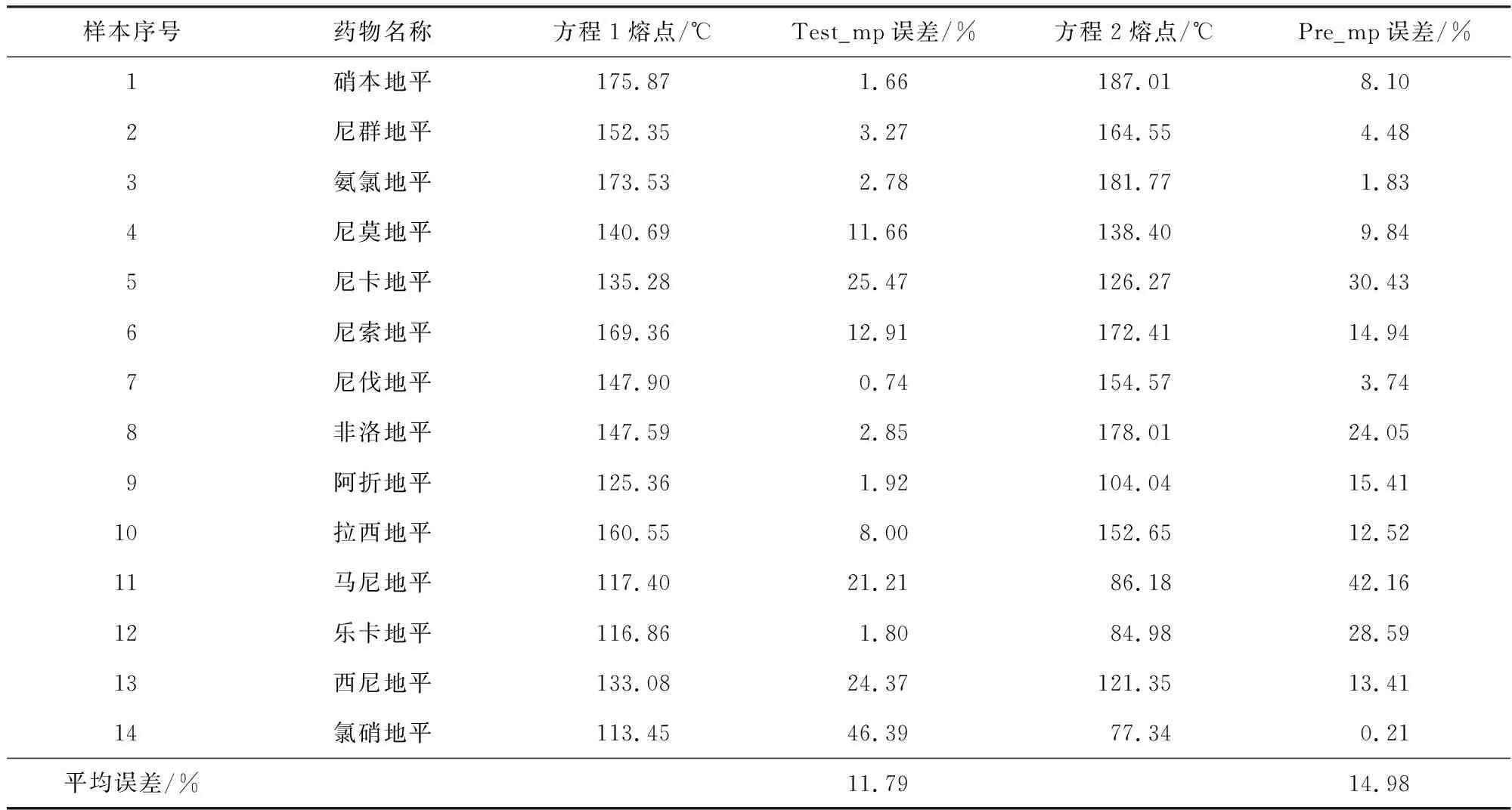
表2 回归方程法熔点计算值及误差Tab.2 Calculation values of RE method and errors

其余4组验证数据见表3。

表3 回归方程法熔点预测值及误差验证

3.2 神经网络程序运行结果

神经网络法熔点计算值及误差见表4。

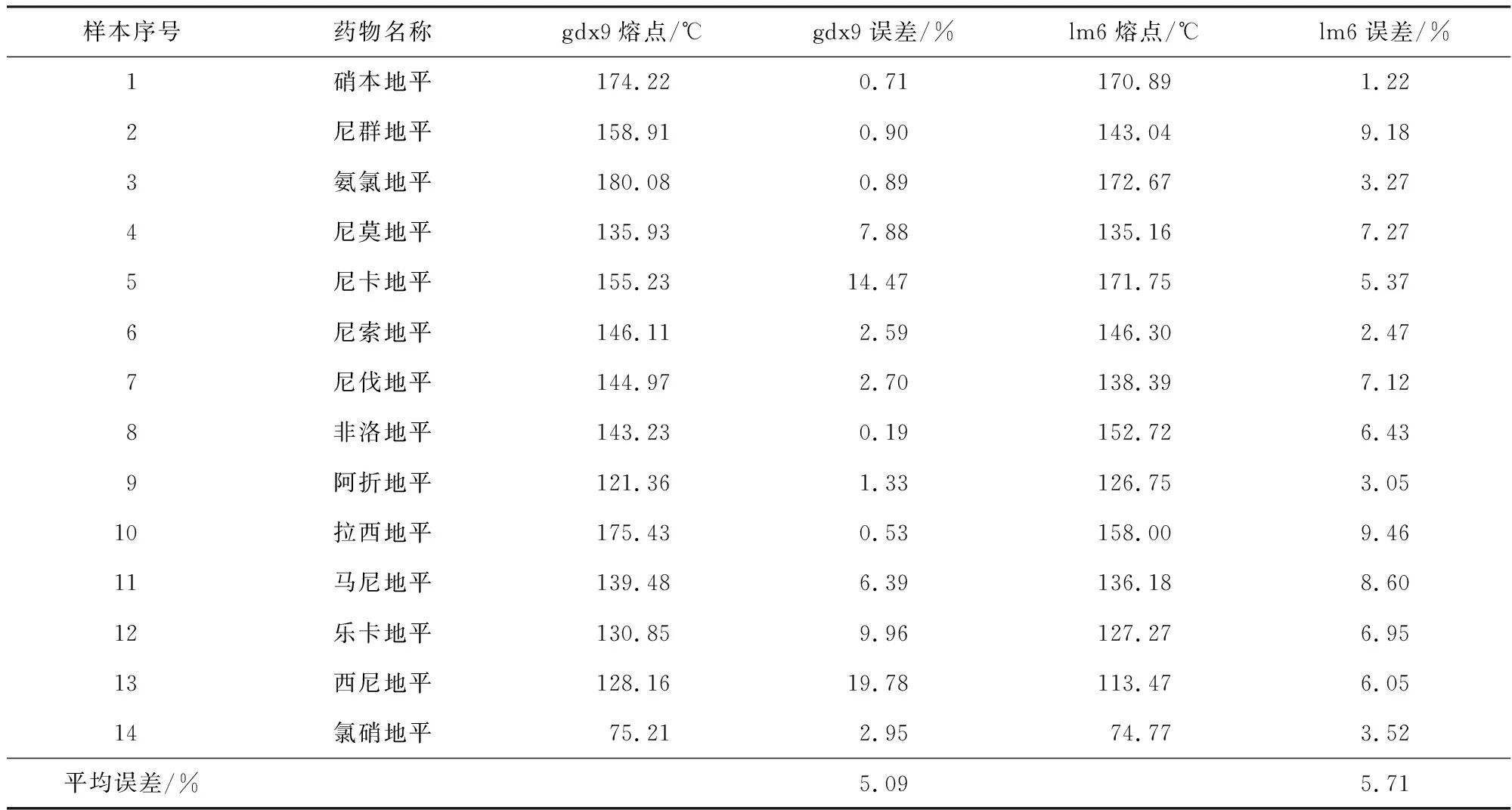
表4 神经网络法熔点计算值及误差

其余4组验证数据见表5。

表5 神经网络法熔点预测值及误差验证

4 结果与讨论

以上数据的结果表明，重新拟合的回归方程比文献[4]中方程更适合于计算地平类药物的熔点。但回归方程法预测结果与实验值比较平均误差在10%左右，而神经网络方法平均误差在5%左右，人工神经网络预测值的结果比回归方程更接近实验值。以上2个方法若进一步完善也可以对其他药物熔点进行更精准的预测，为进一步研究药物的其他理化性质及药物活性提供帮助。而其中的BP神经网络具有设计简单的优点[15]，具有较好的预测和泛化能力，为复杂、高度非线性问题的解决提供了途径。因此，BP神经网络可作为药物构效关系及计算机辅助药物设计的有效方法。

用MATLAB处理数据比较方便，而且能进行非线性拟合。作为高级计算机语言，MATLAB具有强大的计算能力，它将成为药物科研人员进行数据处理及试验设计的得力助手。

参考文献/References：

[1] 宋 倩,梅向东,宁 君. 生物电子等排原理在农药与医药开发中的应用[J]. 河北工业科技,2009,26(2):131-136.

SONG Qian, MEI Xiangdong, NING Jun. Application of bioisosterism in pesticide and medicine development[J]. Hebei Journal of Industrial Science and Technology, 2009,26(2):131-136.

[2] HECHT D, CHEUNG M, FOGEL G B. QSAR using evolved neuralnetworks for the inhibition of mutant PfDHFR by pyrimethamine derivatives[J]. Biosystems, 2008, 92(1): 10-15.

[3] FOMENKO I, DURST M, BALABAN D. Robust regression for high throughput drug screening[J]. Computer Methods and Programs in Biomedicine, 2006, 82:31-37.

[4] 周燕平, 焦 健, 周先锋, 等. 碳酸酐酶XIV抑制剂的定量构效关系研究[J].华中师范大学学报(自然科学版), 2010, 44(4): 618-622.

ZHOU Yanping, JIAO Jian, ZHOU Xianfen, et al. QSAR studies of sulfonamides as the carbonic anhydrase XIV inhibitors by artificial neural network-based transformation for nonlinear partial least-square regression[J]. Journal of Huazhong Normal University (Natural Sciences),2010,44(4):618-622.

[5] LEOW J L, BARON R, CASEY P J, et al. Quantitative structure-activity relationship (QSAR) of indoloacetamides as inhibitors of human isoprenylcysteine carboxyl methyltransferase[J]. Bioorganic and Medicinal Chemistry Letters, 2007, 17(4): 1 025-1 032.

[6] HEMMATEENEJAD B, SHAMSIPUR M. Quantitative structure electrochemistry relationship study of some organic compounds using PC-ANN and PCR[J]. Internet Electronic Journal of Molecular Design, 2004, 3(6): 316-334.

[7] 周 鲁,夏昆华. 喹诺酮类化合物的定量构动关系[J].华西药学杂志, 2006, 21(5): 433-435.

ZHOU Lu, XIA Kunhua. The quantative structure-pharmacokinetic relationship of quinolones compounds[J]. West China Journal of Pharmaceutical,2006, 21(5): 433-435.

[8] 陈国华,陆 瑶,陈 虹. 基于逐步回归所得变量集的遗传反向传播神经网络的QSAR研究[J]. 计其机与应用化学,2010,27(9):1 257-1 262.

CHEN Guohua, LU Yao, CHEN Hong. The QSAR study of backpropagation neural network using genetic algrithm based on variable pool selected by stepwise linear regression[J]. Computers and Applied Chemistry,2010,27(9):1 257-1 262.

[9] 堵锡华,陈 艳,唐自强,等.抗糖尿病新药熔点的定量构效关系研究[J]. 南京工业大学学报,2006,28(2):98-100.

DU Xihua, CHEN Yan, TANG Ziqiang, et al. QSPR research for melting point of new antidiabetic drugs[J]. Journal of Nanjing University of Technology,2006,28(2):98-100.

[10] 高鸿斌,张永强,张 佳. BP-神经网络算法在分布式VOD系统流量预测中的应用[J]. 河北科技大学学报, 2001, 22(3): 23-26.

GAO Hongbin, ZHANG Yongqiang, ZHANG Jia. Applicationof BP-neural networktonetwork-flow predictionof distributed VOD system[J]. Journal of Hebei University of Science and Technology, 2001, 22(3): 23-26.

[11] HANGAN M T, DEMUTH H B, BEALE M. Neural Network Design[M].Beijing: China Machine Press,2002.

[12] KAHANER D, MOLER C B, NASH S. Numerical Methods and Software[M]. Englewood Cliffs: Prentice Hall, 1989.

[13] SMITH B T, BOYLE J M, DONGARRA J J, et al. Matrix Eigensystem Routines-EISPACK Guide[M]. 2nd ed. New York: Springer-Verlag, 1976.

[14] 郝平娇, 李士雨. 浅谈MATLAB在化工计算中的应用[J]. 计算机与应用化学, 2000,17(4): 371-374.

HAO Pingjiao, LI Shiyu. Applications of MATLAB in chemical engineering calculating[J]. Computers and Applied Chemistry, 2000,17(4): 371-374.

[15] 冯 剑. MATLAB在化工计算中的应用[J]. 化学工程师, 2008, 22(5): 25-27.

FENG Jian. Applications of MATLAB in chemical engineering calculating[J]. Chemical Engineer, 2008, 22(5): 25-27.