基于单元应变模态差和RBF神经网络的网架损伤检测方法
张丽梅,刘卫然,张立伟,,杜守军,张 扬
(1.河北科技大学建筑工程学院,河北石家庄 050018;2.中国人民武装警察部队学院基建办公室,河北廊坊 065000)
网架结构具有刚度大、自重轻、受力合理、抗震性能好等优点,被广泛用于工业和民用建筑当中。网架结构日益广泛应用的同时,倒塌事故时有发生[1-2]。例如,1978年美国康涅狄格州哈特福德市中心体育场(正放四角锥网架结构)由于突降暴雪引起压杆失稳倒塌;1997年中国深圳国际展览中心(螺栓球节点网架)由于暴雨后屋面积水过多倒塌[3]等。为了及时、准确发现结构安全隐患,减少盲目维修所消耗的大笔资金,对网架结构进行检测变得十分重要[4]。近年来,国内许多学者在网架损伤识别方面做了大量工作,如宋玉普等利用模态应变能和BP神经网络对一个正放四角锥网架结构做了单个损伤位置识别和损伤程度的判定,但BP神经网络对损伤程度判断不够准确[5];研究人员利用单元应变模态差对一个正放四角锥网架结构做了损伤位置的识别,并指出可根据损伤单元应变模态差值大小来初步判断损伤程度,但并没有对多损伤位置及其程度做出定量的判定[6-7]。
综上所述,找到一个能够进行网架结构杆单元损伤定位和损伤程度定量判断的有效方法是亟需解决的问题。美国Purdue大学的VENKAT和CHAN教授最早应用神经网络进行损伤识别[8]。通常采用的BP神经网络存在局部极小和收敛速度慢等缺点,影响到了损伤识别的效果,而径向基函数(radical basis function,简称RBF)神经网络则在一定程度上克服了这些问题[9]。因此,笔者首先用杆单元应变模态差作为损伤指标识别网架损伤位置,然后用RBF神经网络进行网架损伤程度的定量判定,并将该方法用于一个正放四角锥网架和蜂窝形三角锥网架结构的杆单元损伤检测研究。
1 基于杆单元应变模态差的损伤识别理论[6]
鉴于网架结构中杆件主要为轴向受力,而空间杆单元是仅能在垂直于横截面方向传递轴力的一种结构单元,故采用两节点空间铰接杆单元,假定杆单元处于小应变状态,由单元两端节点位移求得杆单元应变[10]。忽略非线性(即高阶项)影响,可得由两端节点i,j所组成的空间杆单元k的应变εk表达式为
εk=[(uj-ui)(xj-xi)+(vj-vi)(yj-yi)+(wj-wi)(zj-zi)]/L2。
(1)
上述各表达式中,xi,yi,zi以及xj,yj,zj分别为i,j节点在三维整体坐标系中的坐标;而ui,vi,wi以及uj,vj,wj分别为i,j节点在三维整体坐标系中的位移。
根据网架结构某阶的节点位移模态,运用式(1)即可求出相对应的杆单元应变模态。那么,损伤识别指标单元应变模态差就可以表示为
(2)
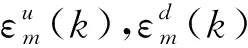
2 RBF神经网络的基本理论
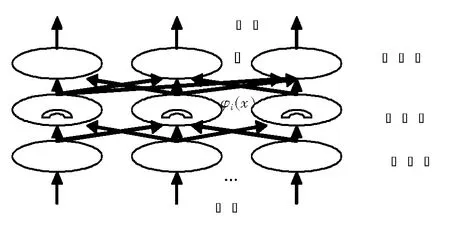
图1 RBF网络结构图Fig.1 RBF neural network structure
RBF神经网络[11]是一种具有3层单向传播的前馈网络,是20世纪80年代末由J. Moody和C. Darken提出的网络模型,它模拟了人脑中局部调整、相互覆盖感受野,是一种局部逼近网络,已经证明它能以任意精度逼近任意函数,其拓扑结构如图1所示。
RBF神经网络隐含层节点传输函数为径向基函数,即隐含层节点对输入产生局部响应,为此RBF神经网络常被称为局部感受野网络。径向基函数有多种形式,常见的是高斯函数,如式(3)所示:
(3)
式中‖xp-ci‖为欧式范数;c为高斯函数的中心;σ为高斯函数的方差;p=1,2,…,P;i=1,2,…,h。
设d是样本的期望输出值,那么基函数的方差为
(4)
学习算法具体步骤如下:
1) 基于k-均值聚类方法求取基函数中心c。
2) 求解方差σi。 该RBF神经网络的学习算法σi表达式为
(5)
式中cmax为所选取中心之间的最大距离。
3) 计算隐含层和输出层之间的权值。 隐含层至输出层之间的神经元的连接权值可以用最小二乘法直接计算得到,计算公式如下:
w=exp(‖xp-ci‖2)。
(6)
在RBF网络训练中,确定隐含层神经元数目的基本原理是通过核对输出误差使得网络自动增加神经元数量。通过不断修改权值向量,一直达到误差要求或者是最大隐含层神经元数为止。所以,RBF网络具有结构自适应确定、输出与初始权值无关等特性,因而在结构损伤识别方面和模式识别方面都体现出良好的优势。
具体的实施过程如下:首先通过有限元计算得到不同情况下的杆单元应变模态,以损伤前后的杆单元应变模态差作为参数定位损伤位置;然后以不同损伤前后的杆单元应变模态差作为训练样本,利用newrb函数作为仿真函数,进行训练直至收敛,SPREAD值取1.5。将某一种工况下的杆单元应变模态差值作为输入值,经过网络映射作用来判断结构损伤程度。
3 网架结构损伤检测的数值模拟分析
3.1 正放四角锥网架损伤检测的数值模拟
图2所示为正放四角锥网架结构,其弹性模量E=2.06×1011Pa,泊松比μ=0.3,杆件面积0.000 05 m2,钢材密度7 850 kg/m3。上弦有36个节点,下弦有25个节点,杆长1 m,高度0.7 m,分别对37,39,41,57,59,61下弦节点固定。在ANSYS中建模,选用两节点线性空间杆单元LINK8模拟网架杆件,结构共有61个节点和200个单元。进行模态分析时,采用质量集中法构造质量矩阵,忽略阻尼的影响,同时假定结构损伤不引起质量改变[12]。损伤工况见表1,其中工况1~工况6为单损伤工况,工况7为同时出现2处损伤的工况,工况8为3处损伤同时存在的工况。

图2 网架结构模型Fig.2 Model of space truss

参数工况1工况2工况3工况4工况5工况6工况7工况8损伤单元(连接节点)11(13~14)82(38~43)106(3~38)118210611,8211,82,106损伤程度10%10%10%30%30%30%30%,40%30%,40%,50%
应用一阶单元应变模态差对上述8种工况进行损伤识别,结果见图3。
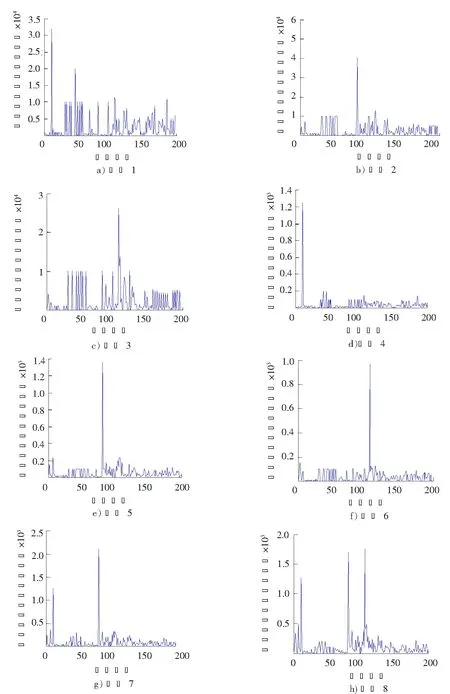
图3 8种工况下的一阶单元应变模态差Fig.3 First elemental strain mode difference of 8 damage cases
由图3可知:单元应变模态差作为网架结构损伤因子可以比较准确地识别损伤位置;由工况1和工况4、工况2和工况5、工况3和工况6对比可知,同一损伤位置不同损伤程度情况下,随着损伤程度的增大,单元应变模态差值也增大。
对于单损伤情况,利用不同损伤(损伤程度分别为5%,10%,20%,30%,40%,50%,60%,70%,80%)前后的杆单元应变模态差作为训练样本,利用newrb函数作为仿真函数,进行训练直至收敛。然后将表1中某一具体工况的杆单元应变模态差值作为输入值,经过网络映射作用来判断结构损伤程度,结果见表2。

表2 神经网络对损伤程度的输出结果(工况1~工况6)
对于多损伤情况,与单损伤情况类似,利用不同损伤前后的杆单元应变模态差作为训练样本,训练样本见表3,利用newrb函数作为仿真函数,进行训练直至收敛。然后将表1中某一具体工况的杆单元应变模态差值作为输入值,经过网络映射作用来判断结构损伤程度,结果见表4。

表3 多损伤杆件损伤程度训练样本

表4 神经网络对工况7和工况8损伤程度计算的输出结果
从表2、表4可以看出:经过RBF神经网络的学习,工况1~工况6的单损伤情况误差最大值是8.1%,多损伤工况7和工况8的误差最大值为5.2%,能够确定损伤杆件的损伤程度。并且损伤越严重,损伤程度的判定误差越小,损伤30%以上的杆件损伤程度判定误差小于2%。
3.2 蜂窝形三角锥网架损伤检测的数值模拟
图4所示的正六边形蜂窝形三角锥网架结构,网架材料弹性模量为E=2.1×1011Pa,泊松比μ=0.3,杆件面积0.000 05 m2,钢材密度7 800 kg/m3。上弦有37个节点,下弦有27个节点,杆长1 m,高度0.82 m,分别对38,41,47,52,62,63节点固定。结构共有64个节点和233个单元(建模方式及单元选取等与前述相同)。进行模态分析时,采用质量集中法构造结构质量矩阵,忽略阻尼的影响,同时假定结构损伤不引起质量改变。损伤工况见表5。
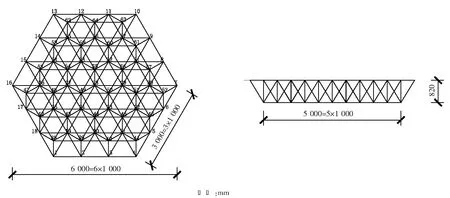
图4 正六边形蜂窝形三角锥网架模型Fig.4 Model of honeycomb-shaped triangular pyramid space truss

参数工况9工况10工况11工况12杆件号(连接节点)2(2~3)30(27~28)170(24~43)2,30,170损伤程度20%40%50%30%,40%,50%
应用式(2)得到一阶应变模态差指标,对上述工况进行损伤识别,结果见图5。

图5 4种工况下的一阶单元应变模态差Fig.5 First elemental strain mode difference of 4 damage cases
将杆件的损伤程度及其所对应的应变模态差作为训练样本,见表6。利用损伤前后的杆单元应变模态差作为输入样本,利用newrb函数作为仿真函数,进行训练。然后将表5中某一工况的杆单元应变模态差值作为输入值,经过网络映射作用来判断结构损伤程度,结果见表7。

表6 杆件损伤程度训练样本

表7 神经网络对损伤程度计算的输出结果
从表7可以看出:经过RBF神经网络的学习工况1~工况3的单损伤情况误差最大值为5%,多损伤工况4的误差最大值为1.72%。因此,结果基本能够确定杆件的损伤程度,并且损伤越严重,损伤程度的判定误差越小,如损伤30%以上的杆件损伤程度判定误差小于2%。
4 结 论
建立了基于应变模态差和RBF神经网络的网架结构损伤识别方法,并将该方法应用于一个正放四角锥网架和一个蜂窝型三角锥网架的损伤识别。结果表明:应变模态差对杆单元的单损伤和多损伤均具有较好的定位能力;经过RBF神经网络对应变模态差的学习,各个单元损伤程度的判定也比较准确,故该方法可以为实际网架结构的损伤检测提供很好的参考。
参考文献/References:
[1] 陈长征,罗跃纲,白秉三,等.结构损伤检测与智能诊断[M]. 北京: 科学出版社, 2001.
CHEN Changzheng, LUO Yuegang, BAI Bingsan, et al. Structural damage detection and intelligent diagnosis[M].Beijing: Science Publisher, 2001.
[2] ZHANG Limei, LI Qilian, ZHANG Yue, et al. Element damage detection of steel truss structure based on the method of wavelet transformation[A]. The 1st International Conference on Electrical and Control Engineering[C]. Wuhan:[s.n.], 2010.6-10.
[3] 张 悦, 杜守军, 张丽梅. 小波奇异性在钢结构损伤检测中的应用[J].河北科技大学学报, 2010, 31(2): 151-157.
ZHANG Yue, DU Shoujun, ZHANG Limei. Application of wavelet singularity to steel structural damage detection[J]. Journal of Hebei University of Science and Technology, 2010, 31(2): 151-157.
[4] MANOJ K, SHENOI R A, COX S J. Experimental validation of modal strain energies based damage identification method for a composite sandwich beam[J].Composites Science and Technology, 2009, 69:1 635-1 643.
[5] 宋玉普,刘志鑫, 纪卫红.基于模态应变能与神经网络的钢网架损伤检测方法[J]. 土木工程学报, 2007, 40(10): 13-18.
SONG Yupu, LIU Zhixin,JI Weihong. Damage diagnosis of spatial trusses based on modal strain energy and neural network[J]. China Civil Engineering Journal, 2007, 40(10): 13-18.
[6] 李永梅, 高向宇, 史升炎,等. 基于单元应变模态差的网架结构损伤诊断研究[J]. 建筑结构学报, 2009, 30(3): 152-159.
LI Yongmei,GAO Xiangyu,SHI Shengyan, et al. Damage diagnosis of space truss based on change of elemental strain model[J]. Journal of Building Structures, 2009, 30(3): 152-159.
[7] 董石麟. 六边形平面蜂窝形三角锥网架的机动分析、受力特性和计算用表[J]. 空间结构, 1995, 1(1):15-23.
DONG Shilin. The kinematic analysis,load-carrying behaviour and design table for triangular pyramid space grids of hex-plane honeycomb pattern[J]. Spatial Structures, 1995, 1(1):15-23.
[8] VENKAT A V, CHAN K. A neural network methodology for process fault diagnosis[J]. Journal of AICE, 1989, 35(12): 1 993-2 002.
[9] 饶文碧, 吴代华. RBF神经网络及其在结构损伤识别中的应用研究[J]. 固体力学学报, 2002, 23(4):477-481.
RAO Wenbi, WU Daihua. RBF and its application for structural damage recognition[J]. Chinese Journal of Solid Mechanics, 2002, 23(4):477-481.
[10] 沈祖炎, 陈扬骥. 网架与网壳[M]. 上海:同济大学出版社, 1997.
SHEN Zuyan, CHEN Yangji. Grid and Reticulated[M].Shanghai: Tongji University Publisher, 1997.
[11] 刘 永, 张立毅. BP和RBF神经网络的实现及其性能比较[J]. 电子测量技术, 2007(4): 77-80.
LIU Yong, ZHANG Liyi. Implementation of BP and RBF neural network and their performance comparison[J]. Electronic Measurement Technology, 2007(4): 77-80.
[12] CAWLEY P, ADAMS R D. The location of defects in structures from measurements of natural frequencies [J]. Journal of Strain Analysis, 1979, 14(2): 49-57.

