周期三对角矩阵求逆的快速算法

唐 达

(上海电机学院 数理教学部， 上海 201306)

周期三对角矩阵求逆的快速算法

唐 达

(上海电机学院 数理教学部， 上海 201306)

利用t向量来求周期三对角矩阵之逆。求逆的运算量为2n2+O(n)乘除法及n2+O(n)加减法。该算法计算量小且计算精度高。若对t向量进行截断、快速求逆，则求逆的计算量仅与n成正比。与现有快速算法相比，清除了电脑内存溢出的情况。文末列出了部分数值算例。

周期三对角矩阵； 逆矩阵； 溢出；t向量； 快速求逆

矩阵

(1)

称为周期三对角矩阵。式中，n为矩阵的阶；在许多科学与工程计算中，如在3次样条周期边界插值、某些抛物型方程差分解、常微分方程周期边值问题的差分解、时间序列分析、图论的特征值分析等领域中，常会使用周期三对角矩阵。因此，对这类矩阵的计算一直是学术界的热点之一；周期三对角阵求逆[1-13]也不例外。文献[1]中所述的解析逆，若用于计算逆阵的全部元素，则其计算量较大；文献[2]中所述的求逆方法，其计算量为3n2+O(n)乘除法及2n2+O(n)加减法；文献[3]中所述求逆方法，其计算量为3n2+O(n)乘除法及n2+O(n) 加减法；文献[5]中提出了4种求解T-1的算法，其最小的计算量也与文献[3]中的相同；文献[6]中所述求逆的计算量为2n2+O(n)乘除法及n2+O(n)加减法，但此算法可能引起电脑计算溢出；文献[7]中提出的算法计算量与文献[6]中的相仿，但亦可能引起电脑计算上溢或下溢；文献[8-9]中三对角矩阵求逆的算法同样可能溢出。

本文利用t向量来求周期三对角矩阵之逆，其计算量为2n2+O(n)乘除法及n2+O(n)加减法，釆用了防止电脑计算溢出的措施。在上述诸多算法中，本文的算法计算量小，算法稳定，且具有较高的精度。若将t向量截断，进行快速求逆，则求逆的计算量仅与n成正比。

1 周期三对角阵求逆

1.1方法概述

在式(1)中，若a1=cn=0，则周期三对角矩阵退化为三对角矩阵，令其为T1。现讨论以下方程的解：

T1t=ej

(2)

式中，ej为n阶单位阵的第j列；t为n维解向量。

为了求解方程(2)，可令

(3)

(4)

(5)

式中，B的第1列为t(1)的尾分量；B的第2列为t(2)的尾分量。B的行相应位于T1的第j及j+1行上。解二阶方程(x1、x2为方程的未知数)：

(6)

为了求T的逆阵，令

T1t(3)=en，T1t(4)=e1

(7)

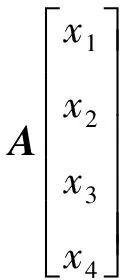
(8)

解出式(8)后，向量

(9)

就是T-1的第j列列向量。令j=1～n，即可求出T-1。

1.2计算量估计

求解式(9)的计算量最大，基本上为整个求逆的计算量。t(1)为t(3)的一段(或一部分)，它们间仅相差一个比例常数。令t(3)与t(1)对应分量之比为k1。计算式(9)时，t(3)可与t(1)对应分量合并计算：

(k1x1+x3)t(1)

同理，t(4)可与t(2)对应分量合并计算：

(k2x2+x4)t(2)

其中，k2为t(4)与t(2)对应分量之比。

上述2段的计算量共需n2+O(n)次乘法；t(3)剩下的一段乘以x1，t(4)剩下的一段乘以x2，共需n2乘法；两者相加需n2+O(n)加减法；因此，计算T-1共需2n2+O(n)乘除法及n2+O(n)加减法。

1.3误差分析

利用式(3)或式(4)计算t向量时，相当于解具有3条对角线的下三角或上三角方程，而解三角形方程组具有较高的相对精度[15-16],故利用式(3)或式(4)计算t向量具有较高的相对精度。求T逆的导出方程只有4阶，其解不会产生太大的误差，故利用本文方法求T-1具有较高精度。

2 防止内存溢出的方法

(10)

(11)

令

(12)

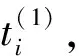
(13)

(14)

用s(1)、s(2)代替t(1)、t(2)后，求T逆的导出方程的系数阵为

(15)

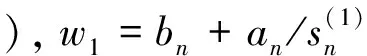
(16)

(17)

从而可求出

如果矩阵T1可均，则根据文献，用本文算法亦可方便地求出T-1，且其计算量比不可约的矩阵小。

3 快速求逆

绝大多数常见的三对角矩阵，其t(1)向量之分量的绝对值是按行序增大的方向递增的；则按行序减小的方向，其绝对值就是衰减的(对t(2)向量也有类似结论)；因此，T-1的元素也具有衰减的性质。文献[17-19]中从不同角度也阐述了逆矩阵元素的衰减性质。在利用式(9)计算T-1的元素时，当t向量之分量衰减到非常小(如相邻两分量的绝对值均小于10-18)时，就对t向量进行截断，将其以后的分量视为零而不予计算，这样做不会影响求逆的精度。因此，求逆的计算量就由与n2成正比减少为与n成正比。此时，T-1是一稀疏矩阵，其非零元的数目不是n2，而是与n成正比。文献[20]中也提出用截断方法来快速求解周期三对角线性方程组，但对截断的条件要求比较苛刻，其实只要t向量具有衰减性，就可根据情况截断。

4 算法歩骤

周期三对角矩阵求逆算法如下：

(1) 输入矩阵T；

(2) 根据式(11)计算s(1)及s(2)；

(3) 根据式(16)计算ui及vi，i=1，2,…,n；

(4) forj=2 step 2 ton-1；

(5) 列出式(15)求逆的导出方程的系数阵，其右端项为(0,1,0,0)T及(0,0,1,0)T；

(6) 计算导出方程之解x1,x2,x3,x4；

(7) 按照式(9)及1.2节所述方法计算T-1的第j及j+1列，其中t向量的各分量根据式(13)、(14)递推求得。在递推时，若检测到相邻两个t分量之值均小于10-18，则进行截断，结束递推；否则，对t(1)、t(3)按行序减小方向一直递推到T的第1行，对t(2)、t(4)按行序増大方向一直递推到T的第n行；

(8) nextj；

(9) 计算T-1的第1列及n列，其导出方程只有二阶，算法与上相仿；

(10) 输出T-1。

5 数值算例

本文算例用PC机CPU为AMD 2.59GB，内存2GB。用Matlab 7.1语言编程计算。每一算例均列出本文算法、文献[3]与文献[7]中算法、Matlab内部函数Inv求逆算法的比较。若令

εi,j=TT-1-I

(18)

式中,I为n阶单位阵；ε为算法误差。则

ε=max|εi,j|，i,j=1,2,…,n

(19)

各例的计算时间及算法误差如表1所示。

表1 算例的计算时间及精度

注： *有2例溢出

例1T的元素为正态分布N(0,1)中之随机数。共计算10次，计算误差及时间t为10次的平均值。

例2式(1)中的T为Toeplitz周期三对角阵，ai=1,bi==6(i=1,2,…,n),ci=5(i=1,2,…,n-1),cn=1。本例取自文献[3]中。

例3Toeplitz周期三对角阵，a1=0.5,cn=0.5,ai=1(i=2，3,…,n)，bi=2.01(i=1,2,…,n),ci=1(i=1,2,…,n-1)。

例4Toeplitz周期三对角阵，a1=1,cn=1,ai=2(i=2,3,…,n),bi=2(i=1,2,…,n),ci=-3(i=1,2,…,n-1)。

在表1中，利用MATLAB Inv函数计算T-1时，T应是稀疏矩阵；其求逆的时间与文献[3]中有较大差别，原因如下： ① 文献[3]中是采用满阵求逆的；② 由于所用Matlab版本不同，故计算的时间差别较大。另外，利用Matlab语言编制的程序是解释程序；若计算量相同，利用Matlab语言编制的程序运行要比其内部函数运行慢得多。

6 结 语

在当今诸多求T-1的算法中，本文的算法计算时间较短，特别对于大型矩阵是这样；计算精度也较高；同时，消除了电脑计算溢出的弊端。因此，本文的算法是一种较好的求T-1的实用算法。

[1] EI-Shehawey M A,EI-Shreef Gh A,AI-Henawy A Sh.Analytical inversion of general periodic tridiagonal Matrices[J].Journal of Mathematical Analysis and Application,2008,345(1): 123-134.

[2] 余承依，陈耀辉，赵立群.求三对角和周期三对角矩阵逆阵的-种新算法[J].长江大学学报： 自然科学版,2010,7(1)： 126-128.

[3] 余承依,陈耀辉.周期三对角矩阵逆的一种新算法[J].数学的实践与认识,2010,40(22)： 192-198.

[4] 陈耀辉,赵立群,余承依.周期三对角矩阵行列式和逆矩阵新算法： 英文[J].数学研究,2011,44(1)： 27-35.

[5] 赵立群.一些稀疏矩阵的逆和行列式的计算[D].漳州： 漳州师范学院，2011.

[6] 袁志杰.有关特殊矩阵的计算问题及性质[D].西安： 西北工业大学，2005.

[7] 杜永恩,陆 全,徐 仲.求分块周期三对角矩阵逆矩阵的新算法[J].计算机工程与应用，2012，48(17)： 41-43.

[8] 冉瑞生,黄庭祝.三对角矩阵的逆[J].哈尔滨工业大学学报,2006,38(5)： 815-817.

[9] 冉瑞生,黄庭祝,刘兴平,等.三对角矩阵求逆的算法[J].应用数学和力学,2009,30(2)： 238-244.

[10] 车 毅,徐 仲,雷小娜.分块周期三对角矩阵逆矩阵的新算法[J].纺织高校基础科学学报,2011,24(1)： 15-20.

[11] 陈 芳,徐 仲.求分块三对角矩阵和分块周期三对角矩阵逆阵的快速算法[J].数学的实践与认识,2005,32(12)： 183-187.

[12] 黄卓红,刘建州.严格对角占优周期三对角矩阵逆元素的上下界估计[J].工程数学学报,2008,25(4)： 703-707.

[13] 袁志杰,徐 仲.严格对角占优周期三对角矩阵逆元素的上界估计[J].工程数学学报,2004,21(8)： 68-72.

[14] 唐 达.三对角矩阵计算[J].高等学校计算数学学报,1997,19(2)： 97-104.

[15] Willkinson J H.代数特征值问题[M].石钟慈,邓健新,译.北京： 料学出版社,2001： 259-261.

[16] 唐 珍.舍入误差分析引论[M].上海： 上海科学技术出版社,1987： 207-209.

[17] Nabben R.Decay rates of the inverse of nonsymmetric tridiagonal and band matrix[J].Journal on Matrix Analysis and Applications,1999,20(3)： 820-837.

[18] Meurant G.A review on the inverse of symmetric tridiagonal and block tridiagonal matrices[J].Journal on Matrix Analysis and Applications,1992, 13(3)： 707-728.

[19] 雷光耀.强主元稀疏阵的近似求逆[J].科学通报,1991,36(8)： 572-574.

[20] 季 青，王能超.解循环三对角线性方程组的追赶法[J].小型微型计算机系统,2002,23(11)： 1393-1395.

Fast Inversion of Periodic Tridiagonal Matrices

TANGDa

(Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China)

In this paper, inversion of periodic tridiagonal matrices is discussed using thetvector. Computational complexity of the inversion is 2n2+O(n) of multiplication and division andn2+O(n) of addition and subtraction. The algorithm has a low computational cost as well as high precision. The computational cost is further reduced to become proportional tonif thetvector is truncated and fast inversed. In contrast to the existing fast algorithms, the out-of-memory errors no longer occur. Numerical examples are presented.

periodic tridiagonal matrix; inverse matrix; overflow;t-vector; fast inversion

2095-0020(2013)05 -0300-05

O 241.6

A

2013-08-19

唐 达(1935-)，男，工程师，主要研究方向为工程数值计算，E-mail: tangdayouxiang@sina.cn