潜泳过程中流体动力特性的数值研究

陈志峰

(浙江建设职业技术学院,浙江 杭州 311231)

潜泳过程中流体动力特性的数值研究

陈志峰

(浙江建设职业技术学院,浙江 杭州 311231)

利用计算流体动力学软件FLUENT，对潜泳阶段水动力性能影响因素进行数值模拟。基于准静态假设得到泳者姿势、泳衣粗糙度、泳衣周围流体流型以及泳衣表面总阻力之间的关系，通过计算结果对比分析获得降低流体阻力的方法，进而提出游泳动作的优化方案，为进一步提高泳者比赛成绩奠了理论基础。

潜泳；水动力性能；FLUENT；数值模拟

1 问题提出

游泳项目研究的首要任务在于优化水的流动特性，使得泳者受到的阻力最小。早期人们主要通过实验的方法来研究泳者姿势、泳速及流体阻力对泳者的影响[1-4]。Berger[5]利用拖曳水池测得手及手臂的阻力系数。Thayer[6]和 Sanders[7]研究了非稳态流动，通过实验证明泳速增加或降低可以明显改变阻力系数的大小。Ta ar[8]通过实验建立了游泳姿势、流体阻力以及蝶泳效果之间的关系。 最近Vennell[9]深入研究了波浪阻力对游泳阻力的贡献，发现当拖曳深度超过0.7m时，波浪阻力可以忽略不计。

尽管实验研究取得了很多重要的结论，但这些结论往往受到实验条件及实验成本的限制。近年来随着计算机科学及建模技术的飞速发展，计算流体动力学(CFD)软件已成为游泳项目研究的重要工具，实践证明CFD软件可以有效地弥补实验研究的不足。Bixler and Schloder[10]利用二维模型研究了水中圆盘加速转动对周围水流的影响。Bixler and Riewald[11]通过对三维手臂模型进行稳态模拟得到手臂阻力及相应的阻力系数，并与实验结果相一致。Rouboa[12]利用二维手臂模型研究了稳态及瞬态情况下，泳者手臂阻力及相应的阻力系数。Gardano和 Dabnichki[13]通过对整个手臂进行数值模拟得到不同肘部夹角下整个手臂受到的阻力及升力，结果与实验数据相一致。Bixler[14]利用三维稳态模型，模拟了潜泳过程中泳者受到的总阻力及周围水的流动特性，通过与实验结果对比，验证了该模型的准确性。Za di[15]研究了潜泳开始阶段及调头阶段头部位置对水动力特性的影响。最近，Za di[16, 17]利用不同的湍流模型对流体流型及流体阻力进行计算，结合实验得出k-ω模型的计算结果较标准的k-ε模型更准确。

本文利用经典计算流体动力学软件FLUENT研究了潜泳过程中泳者姿势及泳衣粗糙度对水动力特性的影响。通过二维稳态及瞬态模拟得到泳者周围流体速度场分布以及总阻力随泳者姿势的变化关系。利用三维稳态模型对头部附近流体速度分布及头部所受总阻力进行数值模拟，通过与二维模拟结果的对比分析，可以看出二维模拟适用于流体特性的定性分析，最后提出潜泳过程中泳者动作优化方案。

2 物理模型及计算方法

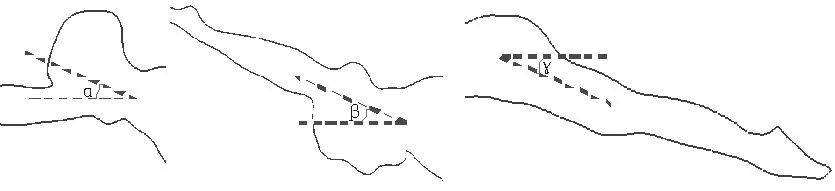
为了研究泳者姿势及泳衣粗糙度对水动力特性的影响，泳速取值为2m/s，泳装粗糙度为0mm，(以下模型如未具体说明，入口速度均为2m/s，且入口速度即为泳速)；以α，β，γ(见图2)均0°时的姿势做为参考姿势。通过改变α，β，γ值来研究泳者姿势对周围流场分布及泳者所受总阻力的影响；粗糙度取0mm和0.5mm，通过对两组数据计算结果的对比分析来研究泳衣粗糙度对泳者所受总阻力的影响。

2.1模型描述及网格划分

(a)

(b)

图1 a中蓝色线条代表泳装，数值计算过程中忽略水波阻力的影响。α，β，γ(见图1 b)分别为头部、手臂及腿部与水平方向的夹角。选取α，β，γ均0时的姿势进行瞬态模拟来研究泳衣表面流场的瞬态特性。

(a)

(b)

图2a矩形区域为计算区域，计算区域比泳者本身大得多，考虑到泳者体型比较曲折，因此采用Gambit中的非结构化网格对计算区域进行划分。为了减轻计算负荷，通过Gambit内部自带的“尺度函数”对泳者周围网格进行细化并确保紊流边界层内包含几层网格，这样划分网格有利于保证泳者周围紊流计算的精度。

进行数值模拟之前，首先要测试网格划分的精度，以确保计算结果与网格数无关。通过测试发现当网格数超过80 000时，泳者所受的总阻力几乎为一常数。这一现象说明计算结果独立于网格解析度，因此该网格划分是合理的。

2.2计算方法

模拟过程忽略自由表面的影响，牛顿型流体流动总控制方程及不可压缩紊流方程描述[19]如下：

连续性方程：

(1)

动量方程：

(2)

Boussinesq假设：

(3)

紊流方程(标准的k- ε模型)：

(4)

(5)

(6)

(7)

为了求解以上控制方程，需要对边界条件做如下设置：入口边界条件为速度入口，出口边界为岀流。计算区域的上下边界设置为对称边界(也可以设置成远场边界)。泳者身体轮廓线设置为无滑移边界，泳装表面设置为壁面并添加粗糙度。 当粗糙度为0mm时，泳衣表面为理想光滑面此时泳装表面无边界层形成。

边界条件与控制方程关联，在FLUENT 求解器中求解。采用二阶离散格式来减少数值耗散误差。紊流模型中，壁面边界条件应设置为“非平衡壁面函数”[11,14-18]。

(a)

(b)

3 结果与讨论

从图3a可以看出涡流主要分布在颈背、脚底以及下巴到胸部之间的区域。从图3b可以看出，流体最大速度主要集中在身体的突出部位，例如鼻尖，头顶以及脚尖等。入口流速对人体总阻力的影响如图4所示。从图4中可以明显地看出作用在泳衣表面的压力、总阻力以及粘滞阻力均随入口流速的增加而增大。

图4 入口流速对泳衣表面总阻力的影响

从图5a可以看出涡流的大小及位置很明显地受头部位置影响。潜泳过程中，头部抬起会在颈部周围产生一个大的回流区，回流区内水速较小，同时在上游腋窝处产生第二个回流区，这一现象与其他研究人员[15]研究结果一致。图5b为泳装所受的总阻力随α的变化关系。为便于对比分析，取壁面粗糙高度为0mm和0.5mm两组数据进行计算。结果显示，两种情况下α为5°时，泳装表面总阻力取得最小值。因此在潜泳过程中，稍微抬高头部位置对于降低流动阻力是很有效的。从图4知潜泳过程中随着泳速的增加粘滞阻力逐渐增大，导致泳装粗糙度对总阻力的影响显著增强。通过对不同粗糙度下总阻力的计算，可以看出粗糙度为0.5mm时泳装表面总阻力增加了5%。

(a)

(b)

(a)

(b)

由图6a可以看出，涡的大小及位置明显地受手臂位置影响。潜泳过程中手臂下移会在颈背、手掌、及脚板附近区域形成涡流，涡流速度较小；然而在头顶及手指附近水流速度则较大。从图6b可以看出，无论手臂抬高或者降低，总阻力随|β|的增加而增大。因此在潜泳过程中，手臂应保持水平。

与图5(b)相比，手臂位置对水动力特性的影响要比头部位置的影响更明显。这是因为手臂保持水平姿势有利于光滑流线沿手臂表面流过，而抬高或降低手臂都会引起复杂的涡流，这不仅增加了手臂的阻力而且扰乱了身体表面流体运动形态，使得身体表面阻力增加，总阻力也随之增加。从图6 (b)可以看出泳装粗糙度对泳衣总阻力的影响依然很明显。

(a)

(b)

从图7a中可以看出，涡流的大小及位置受腿部位置影响，在潜泳过程中腿部下移会显著改变身体突出部位附近流线分布。从图7b中可以看出，泳衣表面总阻力随γ的增加而迅速增大，当腿部保持水平时总阻力最小，通过对不同粗糙度下总阻力的计算，可以看出粗糙度为0.5mm时泳装表面总阻力增加了5%。

(a)

(a)

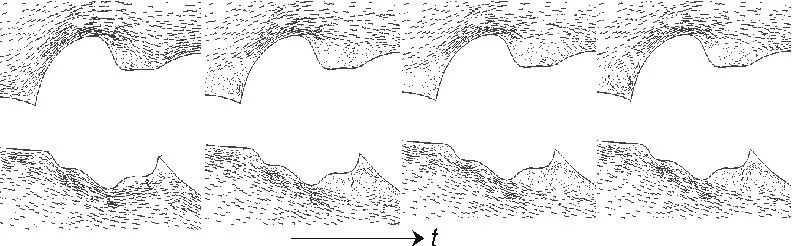
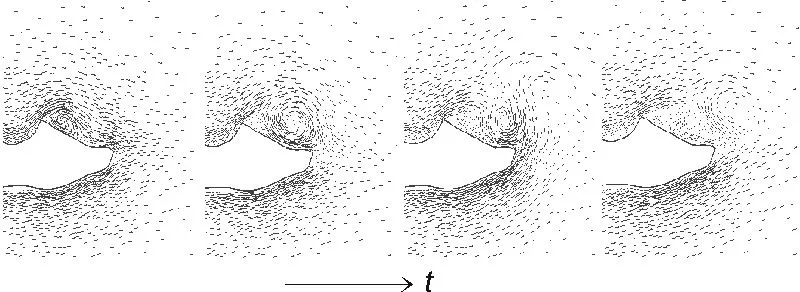
从图8a可以看出下巴及胸部周围涡流随着时间的推移向后移动。初始阶段下巴和胸部间的涡流很不明显，随着时间向右进行此处涡流开始逐渐形成、发展，最终达到稳定形态向后滑移。图8b为典型的涡流形成、发展及分离过程。从图8中可以明显地看出，涡流形成于脚跟附近，然后沿脚尖方向向前运动，强度不断增加，涡流移动的同时在脚跟周围又形成新的涡流，最终涡流从脚尖处脱离顺流而下。

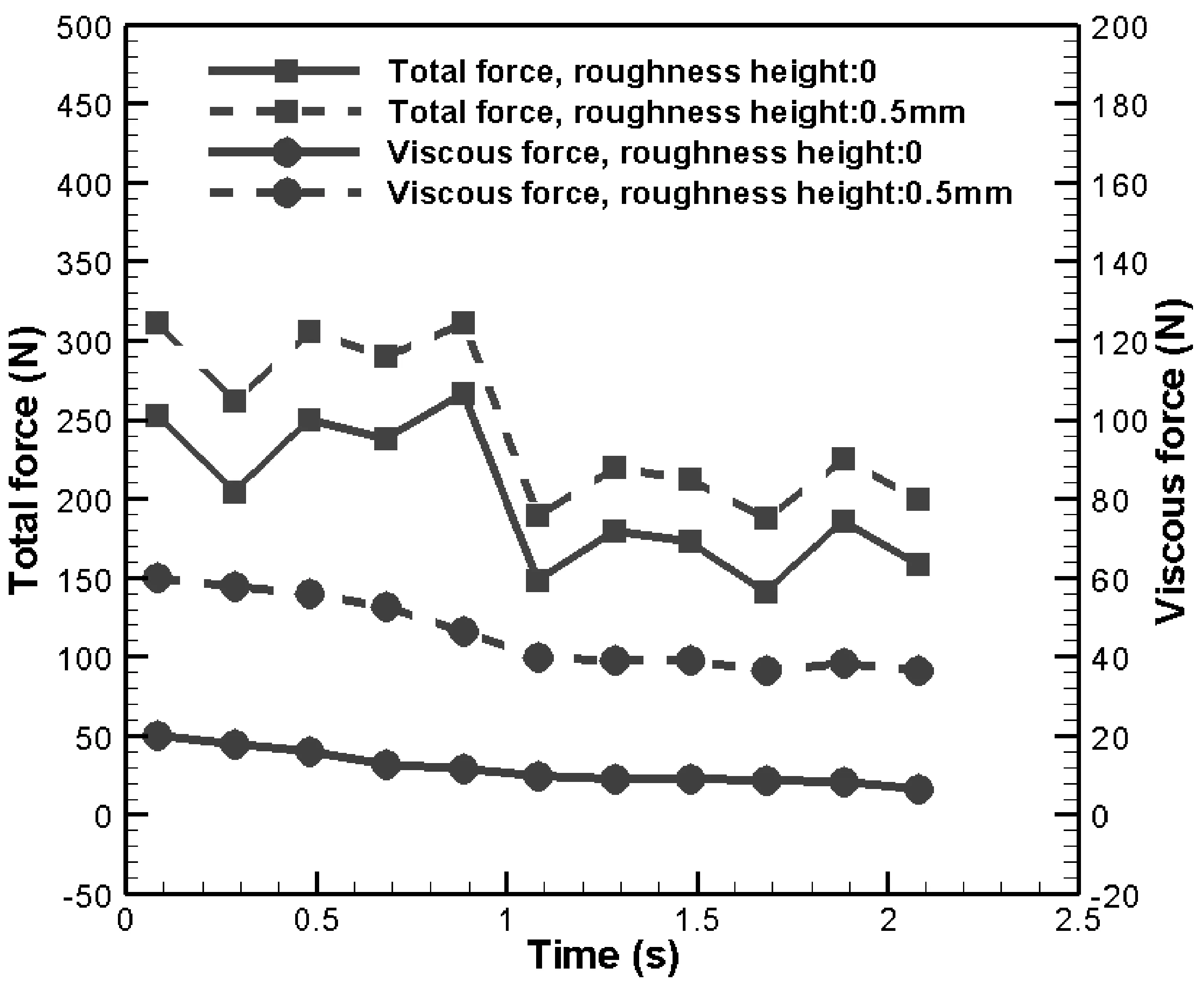
图9 泳衣表面阻力随时间的变化关系

由图9可以看出，泳衣粗糙度为0mm时，表面总阻力在180N到280N之间变化。

这样的结果是合理，这是因为泳衣表面阻力明显受泳者周围涡流瞬态特性的影响。与稳态模拟相比，瞬态模拟中泳装粗糙度对总阻力的影响更加明显。通过对图中两条红色折线数据对比分析可以看出，粗糙度为0.5mm时粘滞阻力增加了近2倍，这是因为泳衣表面流体流型非常复杂，以至于泳装粗糙度的微小变化即可显著地改变水流流动特性，从而影响泳衣表面粘滞阻力的变化。

图10a中的箭头代表速度矢量，从图10中可以看出头部后面有涡流产生，头顶及下巴附近水流速度较大。

(a)

(b)

图10b描述了二维及三维模型中泳衣所受总阻力随α的变化关系。从图10b中可以看出两条曲线的变化趋势相同；当头部与水平方向的夹角α保持在5°左右时，总阻力最小；当α增大或者减少都会使总阻力增加，因此在潜泳过程中应保持头部稍微抬起使得α尽量维持在5°左右。

在此需要指出的是，三维模型下流体运动更加复杂同时还要求计算结果独立于网格解析度，因此需要大量不规则网格，这对计算机内存销耗非常大，现有设备尚无法进行计算，因此我们仅给出了头部区域的三维模拟结果，在下阶段的研究中将结合实验验证给出完整的三维模拟结果。

4 结 论

本文采用瞬态及稳态模型研究了潜泳过程中泳者姿势及泳装粗糙度对水流动特性的影响，可以看出泳者姿势对身体阻力影响很大，优化后的姿势应该是头部稍微抬起，手臂及腿应保持水平。为了降低潜泳过程中水的阻力，应尽量降低泳衣表面的粗糙度。此外瞬态分析表明，头部周围涡流特性随时间变化，脚跟附近出现涡流生成、发展及分离的现象。涡流的非稳态特性引起泳衣表面总阻力随时间的变化。通过二维及三维模拟结果可以看出泳者头部所受总阻力随α的变化趋势一致，因此可以用简化的二维模型对流体流动过程做定性分析。以上数值模拟结果给出了实验所不能提供信息，这就为进一步改进游泳运动员动作奠定了理论基础。

[1] Huijing P A,Toussaint H M,Clarys J P,Groot G,Hollander A P,Vervoorn K,MackayR,Savelberg H H C M.“Active drag relatedto bodydimensions”[M].In:Ungerechts Reischle K. Wilke K(eds.).1988：31-37.

[2] Kolmogorov S V,Duplishcheva O.Active drag useful mechanical power output andhydrodynamic force coefficient in different swimming strokes at maximal velocity[J].Biomechanics .1992,25:311-318.

[3] Toussaint H M,Roos P E.The Determination of drag in front crawl swimming[J].Biomechanics.2004,37:1655-1663.

[4] Toussaint H M,Truijens M.Biomechanical aspects of peak performance in human swimming[J].Animal Biology.2005,25:17-40.

[5] Berger M A,Groot G,Hollande A P.Hydrodynamic drag and lift forces on human/arm models[J].Biomechanics.1995,2:125-132.

[6] Thayer A M.Hand pressures as predictors of resultant and propulsive hand forcesin swimming[D].University of Iowa, Iowa City, Iowa 1990.

[7] Sanders R H.Hydrodynamic characteristics of a swimmer’s hand[J].Applied Biomechanics.1999,15:3-26.

[8] Ta ar R,Sagnes P,Henry C,Dufour A B,Rouard A H.Hydrodynamics optimization inbutterfly swimming:position,drag coefficientand performance[J].Biomechanics.1999,32: 803-810.

[9] Vennell R,Pease D,Wilson B,Wave dragon human swimmers[J].Biomechanics.2006,39:664-671.

[10] Bixler B S,Schloder M,Computational fluid dynamics: an analytical tool for the 21st century swimming scientist[J].Swimming Research.1996,11:4-22.

[11] Bixler B,Riewald S,Analysis of swimmer’s hand and arm in steady flow conditions using computational fluid dynamics[J].Biomechanics.2002,35:713-717.

[12] Rouboa A,Silva A,Leal L,Rocha J.Theeffect of swimmer’s hand/forearm acceleration on propulsive forces generation using computational fluid dynamics[J].Biomechanics.2006,39:1239-1248.

[13] Gardano P,Dabnichki P.On hydrodynamics of drag and lift of the human arm[J].Biomechanics.2006,39:2767-2773.

[14] Bixler B,Fairhurst F,The accuracy of computational fluid dynamics analysis of the passive drag of a male swimmer[J].Biomechanics.2007,6:81-98.

[15] Za di H,Ta ar R,Fohanno S,Polidori G.Analysis of the effect of swimmer’s head position on swimming performance using computational fluid dynamics[J].Biomechanics.2008,41:1350-1358.

[16] Za di H,Ta ar R,Fohanno S,An evalua-tion of turbulence models in CFD simulations of underwater swimming[J].Biomechanics.2009,24:5-14.

[17] Za di H,Ta ar R,Fohanno S,Polidori G.Turbulence model choice for the calculation of drag forces when using the CFD method[J].Biomechanics.2010,43:401-411.

[18] Polidori G, Ta ar R,Fohanno S,Lodini A.Skinfriction drag analysis from the forced convection modeling in simplified underwater swimming[J].Biomechanics.2006,39:2535-2541.

[19] Chen Zhifeng,Fang Haisheng.The effects of Wind and Posture on the Aerodynamic Performance During the Flight Stage of Skiing[J].Biomechanical Engineering.2011,133:1-5.

NumericalStudyoftheHydrodynamicPerformanceDuringUnderwaterSwimming

CHEN Zhi-feng

(Zhejiang College of Construction, Hangzhou 311231, China)

Numerical study is conducted to evaluate the affecting factors of the hydrodynamic performance during the stage of underwater swimming, which was simulated on computation fluid dynamics commercial software FLUENT. Based on a quasi-steady state assumption, the relationships among swimmer postures, wetsuit roughness, stream pattern near body, and the total force are predicted, then make a comparative analysis of the results, by which methods to lower the total force are obtained ,at last,optimum schemes on swimming stroke are present, which build a theoretical basis for the further improvement of competition results.

underwater swimming；hydrodynamic performance；FLUENT；numerical simulation

1004-3624(2013)04-0073-05

G861.5

A

浙江省教育技术研究规划课题(JB029)

2013-04-15

陈志峰(1977-)，男，浙江义乌人，硕士，讲师，研究方向：运动生物力学.