海量地震数据叠前逆时偏移的多GPU联合并行计算策略
孔祥宁,张慧宇,刘守伟,李晶晶
(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京 211103;2.同济大学,上海 200092;3.中国石油大学(华东),山东青岛 266580)
随着高性能计算机及其应用技术的高速发展,叠前逆时深度偏移方法已经成为对复杂地质体进行成像现实可行的手段,该方法在成像精度上相对于其它偏移方法的优势也被普遍认可[1]。叠前逆时偏移方法直接求解双程微分波动方程,避免了单程波偏移方法中上、下行波的分离,对波动方程的近似较少,克服了偏移倾角的限制,可以有效地处理纵、横向速度存在剧烈变化的地球介质物性特征[2-3]。该技术除了具有成像精度高,不受介质纵、横向速度变化和高陡倾角构造的影响等优点外,甚至还可以利用一些传统处理中作为噪声压制的特殊波场(如多次波、回转波及棱柱波等)进行成像。
叠前逆时深度偏移并不是一个新的理论方法,早在20世纪七八十年代就有学者提出了逆时偏移的基本思想和实现方法[4-6]。虽然RTM 成像精度高,且对速度的适应性强,但是在实际生产中的应用规模还非常小,这主要是由于RTM 对计算量和存储量的需求巨大等瓶颈问题不易解决[7-9]。随着大型计算集群的快速发展,计算需求和成本对RTM 的限制逐渐减小,RTM 的工程化应用已成为可能[10]。近年在高性能计算方面出现的GPU/CPU 协同并行计算技术,迅速成为高性能密集计算发展的趋势。此种异构集群平台非常适合于RTM 等大规模数据的处理[11],与CPU 集群相比,具有投入少,后期运行维护成本低等优点。国内外在基于CPU/GPU 的地震叠前逆时偏移计算方面的研究工作不断取得突破性的成果。Araya-Polo等[12]首先用Cell处理器实现了三维叠前深度逆时偏移;Micikevicius[13]给出了利用GPU 实现高阶有限差分的算法;Darren 等[10]在利用GPU实现逆时偏移方面做了有益的尝试;李博等[14]提出了地震叠前逆时偏移算法的CPU/GPU 实施对策;赵磊等[11]根据CPU/GPU 异构平台计算能力非常强的特点,以牺牲计算量换取存储量和I/O 次数的减少,实现地震叠前逆时偏移计算。
简单地说,GPU/CPU 协同并行计算就是将GPU 和CPU 两种不同架构的处理器结合在一起,组成硬件上的协同并行模式,同时在应用程序编写上实现GPU 和CPU 软件协同配合的并行计算。我们主要介绍采用GPU 多卡联合策略解决GPU显存不足的瓶颈,在GPU/CPU 异构集群平台上实现RTM 的协同并行计算。
1 基本原理
各向同性介质下,RTM 需要直接求解的三维声波方程为
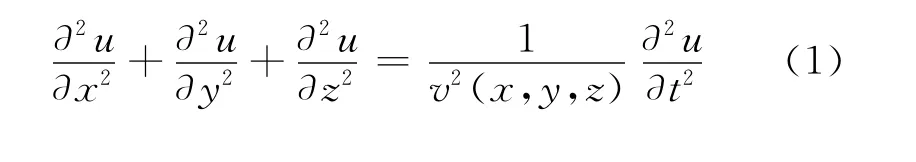
式中:u(x,y,z,t)为地表记录的压力波场;v(x,y,z)为纵横向可变的介质速度。
在求解方程(1)的过程中需要利用合适的成像条件提取成像值。本文中逆时偏移的实现采用了方程(2)所示成像条件,该成像条件考虑了震源波场的照明补偿,较直接的相关成像条件具有较优的保幅特性,可为后续的AVO 等属性分析提供更真实的地震信息。

式中:tmax为最大记录时间;Ss(x,y,z,t)为正向外推的震源波场;Rs(x,y,z,t)为反向外推的记录波场;I(x,y,z)为点(x,y,z)的成像结果;σ为一小常量,以保证方程(2)的稳定性。
逆时偏移的实现流程如图1所示。

图1 逆时偏移技术流程
逆时偏移方法是通过双程波波动方程在时间上对地震资料进行反向外推并结合成像条件实现偏移的,对全波场进行逆时外推,避免了上、下行波的分离,且不受倾角的限制,并能够对任意倾斜构造甚至回转波进行成像[14]。逆时偏移在算法实现上主要包括3部分关键技术,即震源波场的正向延拓、接收点波场的反向延拓和恰当的成像条件。由于震源波场沿时间是正向的,叠前炮记录波场沿时间是逆向的,要将这两个波场做零延迟互相关,就必须要保存其中一个波场,这就是逆时偏移面临的存储量问题。震源波场和检波点波场都根据方程(1)进行双程外推,无论是利用有限差分法求解还是利用伪谱法求解都需要巨大的计算量,这就是逆时偏移面临的计算量问题。
目前,为了解决巨大的存储需求问题,工业界普遍使用的是Check-pointing技术[15],这种方法的核心思想是将偏移过程沿时间分成若干片段,每次偏移其中的一段时间,这样只需存储当前时间片段中的波场即可,而付出的代价是增加0.5倍的计算量。这种方法较有效地减少了存储需求量,但存储量仍然较大,而且I/O 量非常巨大,极大地影响了计算效率。为此,我们采用震源波场重构的存储策略,即先将震源波场正向外推到Tmax,外推过程中只存储边界波场信息,然后在检波点波场进行逆推时作为边界条件再重构震源波场,再应用成像条件。这种方法同样增加了0.5倍的计算量,但存储量和I/O 量均得到了大幅度的降低。
对于计算量太大这一瓶颈问题,我们引入了GPU/CPU 联合并行的计算策略。无论是波场的正向延拓还是反向延拓,我们都采用了显式有限差分的计算方法,该方法计算密度非常高,并行性非常好,适用于利用GPU 进行并行计算。通过高性能的GPU/CPU 异构集群平台,充分利用GPU 在科学计算方面的强大优势,建立了实用的叠前逆时深度偏移成像技术流程。
2 RTM 并行计算策略
地震叠前逆时深度偏移是典型的大计算吞吐、大数据吞吐的地震数据处理任务,须采用并行计算的策略来实现其实际应用;而RTM 中所固有的可分解性和线性叠加性质,使其具有良好的并行能力,这为我们实现RTM 的并行计算提供了条件。GPU/CPU 协同并行计算就是将GPU 和CPU 两种不同架构的处理器结合在一起,组成硬件上的协同并行模式,同时在应用程序编写上实现GPU 和CPU 软件协同配合的并行计算。CPU 主要负责GPU 的控制、数据的准备、数据在节点间的发送与接收等,即进行并行控制;GPU 主要进行RTM 中最耗时的波场外推计算及进行并行计算。有限差分法波场外推是典型的单指令多数据的计算,非常适合用GPU 处理。
设计并行算法首先要选择合适的并行粒度。并行算法根据计算任务的大小可分为粗粒度并行算法、细粒度并行算法和介于二者之间的中粒度并行算法。并行粒度的选择在对物理问题并行性分析的基础上,必须兼顾通讯开销、计算与通讯的重叠程度、负载均衡及容错处理等并行程序设计中的关键问题。
2.1 CPU 上的并行设计
RTM 计算以一个炮集数据为基本计算单元,每一炮数据的偏移成像都是一个相对独立的作业,计算时相互之间不需要或很少需要进行数据交换,因而具有很强的并行性,很适合作为一个独立的并行作业。这是典型的SPMD 算法,即在不同结点上用相同的程序对不同的数据体进行计算。不同节点上的计算任务不是同时开始或结束,各个节点任务的开始与结束和其它节点任务的开始与结束无关,并且不同节点上相同程序不同数据的计算或通信也不是同时进行的。每个节点上每一份作业做完,即得到一份新的作业,便又立即开始执行,这大大增加了计算相对于通信的比重,有效地提高了计算效率。考虑到计算节点间性能的差异及多用户运行环境下最大限度地发挥各个节点的计算效率,我们采用了“任务池”分配方式(图2)的主从并行计算模式来保证RTM 计算时的动态负载均衡。
具体的实现过程是:首先,主进程读取计算参数,计算出RTM 成像的总炮数及相关参数,形成“任务池”;然后,各个从进程到主进程取得所要计算的“任务”,进行RTM 成像计算,将每一炮的成像结果保存在本地磁盘的临时文件中,同时从主进程获取新的“任务”,直到所有的“任务”完成;最后,收集各个从进程的计算结果,并输出最终RTM 成像结果。

图2 实现RTM 的主从并行计算模式
2.2 GPU 上的并行设计
GPU 上实现逆时偏移计算主要包括两项关键技术,一是并行策略,二是存储策略。
我们知道,GPU 上的并行计算属于细粒度并行算法,它的并行结构分为3个层次:线程、线程块以及由线程块组成的线程网格,它可以针对数据体中的每个元素进行并行计算,力度之细是CPU 无法比拟的。我们所实现逆时偏移的主要计算热点为有限差分计算,有限差分算子可以抽象为向量乘法问题。因此,将整个RTM 计算过程中计算量最密集的波场延拓通过GPU 并行策略实现,最能提高计算效率。需要注意的是,利用高阶有限差分法计算需要大量的内存读写,以三维时间二阶、空间8阶差分网格为例,每计算一个网格点的值都需要读取周围25个网格点的数据,内存读取冗余度非常高。为此,我们考虑借用GPU 提供的片内存储器共享内存来降低数据读取延迟,提高计算效率[17]。目前最新的一款nVidia Tesla Kepler K20X 图形处理器有2 688个核心,可以同时处理2 688个样本,尤其是针对RTM 的单精度计算,具有非常高的处理效率。
我们主要采用的存储策略是震源边界波场存储与重构。在波场正传时,记录每一个计算时间步的震源波场的6个面,当记录波场逆向外推时再由波动方程及其边值条件、初值条件重构空间震源波场。其公式表示为

这样节省了大量的存储空间,降低了数据的通讯量,提高了计算效率。
此外,由于GPU 的显存有限,当计算一炮数据所需空间超过GPU 一块卡的显存容量时,则无法进行逆时偏移计算。为打破这一限制,我们采用了GPU 多卡联合计算模式,即将GPU 多卡进行捆绑,共同进行单炮RTM 计算,如图3所示。
为了使算法满足任意大规模地震数据的处理,我们设计了利用内存作为中转站的数据交换机制,这种机制不限定每个节点GPU 卡的数量,根据计算需求动态规划每炮计算需要的节点数和GPU卡的数量。这样,一次数据交换,就需要4次GPU与CPU 之间的数据传输以及一次CPU 内存间的传输,其中CPU 与GPU 的数据I/O 具有一定的访存延迟。
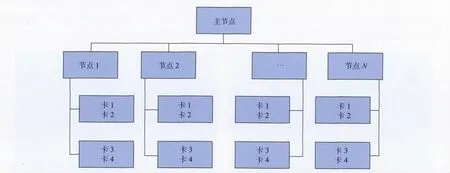
图3 GPU 多卡联合计算模式
通过GPU 多卡处理可以解决GPU 显存不足的限制,但另一方面引入了通讯量的问题。利用多卡联合计算一炮数据,意味着将一个炮数据体分别用不同的GPU 卡计算,那么在计算过程中就需要卡与卡之间的数据交换,从而增加了GPU 卡之间的I/O 通讯量。为了优化GPU 卡间的数据通讯,我们采用数据I/O 隐藏策略,将数据体按照GPU显存进行划分,每块卡上的又可分为独立计算部分和边界的重叠计算部分。计算过程分为两步进行(图4):①对重叠数据部分进行计算;②在计算独立数据部分的同时,进行卡与卡之间重叠数据的交换。通过数据计算与数据I/O 通讯的同时进行,实现了数据I/O 的隐藏策略。在新一代的GPU架构中(Fermi架构)增加了GPUDirectTM技术,该技术可以直接读取和写入CUDA 主机内存,消除不必要的系统内存拷贝和CPU 开销,还支持GPU之间以及类似NUMA 结构的GPU 到其他GPU内存直接访问的P2P 的DMA 直接传输。这些功能为未来版本的GPU 和其它设备之间的直接点对点通信奠定了基础。
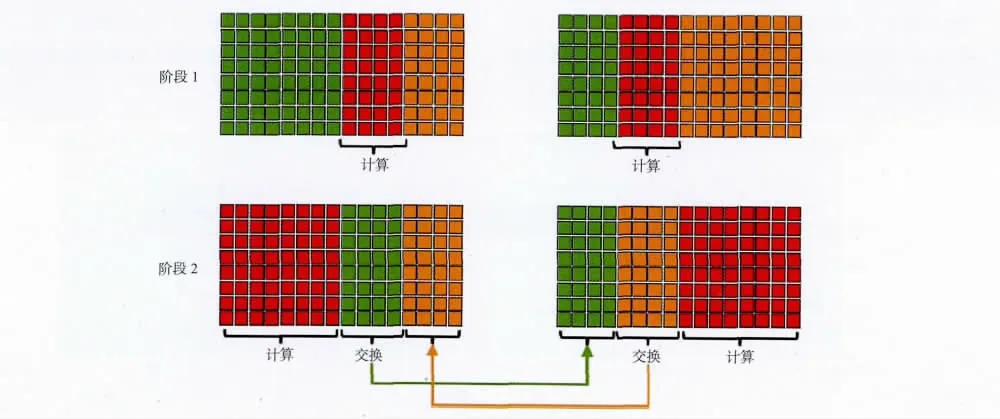
图4 数据I/O 的隐藏策略
3 应用实例
我们应用某海上三维地震数据对上述方法进行测试。该地震数据采集采用双震源激发,共6条接收线,最大接收道数408,最大偏移距5 100m,道距12.5m,最大反射长度6 144ms,采样间隔2ms。处理面元12.5m×12.5m。
本次试处理的目标成像范围约84km2,为保证足够的偏移孔径,资料输入面积约为185km2,一共有45 061炮,数据量367G。偏移网格为:Ny=997(dy=12.5m),Nx=1 188(dx=12.5m),Nz=601(dz=8m);偏移孔径为xapert=7 000m,yapert=7 000m;采用子波为雷克子波,主频30Hz;时间延拓长度为6.0s,步长0.5ms。在CPU 平台进行叠前逆时深度偏移的单炮用时约为26.2h,而在GPU平台实现叠前逆时深度偏移的单炮用时约为0.43h。图5为基于CPU 平台和GPU 平台的逆时偏移剖面对比结果,可以看出,两者成像效果相当,均能对岩丘边界进行较好的成像,清晰刻画出岩体与周围地层的接触关系。

图5 某海上三维地震数据RTM 偏移剖面
在GPU/CPU 异构平台下,RTM 单炮的计算用时基本不超过0.47h,且主要集中在0.3~0.4h(图6)。试处理结果表明,利用CPU 实现逆时偏移耗时巨大,而利用GPU 计算则大大减少了计算周期,取得了60倍的加速比。因此,在GPU/CPU 平台及多GPU 联合并行计算策略的支持下,三维叠前逆时深度偏移已经可以实现海量地震数据的实际生产性处理。

图6 基于GPU/CPU 异构平台的RTM 每炮计算时间
4 结束语
通过震源波场重构策略及GPU/CPU 协同并行计算,在保证成像品质的前提下,充分发挥了GPU 的计算优势,极大地提高了RTM 的计算效率。而GPU 多卡联合处理技术能够有效地解决GPU 显存不足这一瓶颈。实际资料的处理结果表明,借助于GPU/CPU 异构集群后,RTM 这种高精度成像方法能够达到实际应用的要求,有利于对复杂地质体进行准确、有效地成像。
[1]刘定进,杨勤勇,方伍宝,等.叠前逆时深度偏移成像的实现与应用[J].石油物探,2011,50(6):545-549 Liu D J,Yang Q Y,Fang W B,et al.Realization and practices of pre-stack reverse-time depth migration[J].Geophysical Prospecting for Petroleum,2011,50(6):545-549
[2]陈可洋.基于高阶有限差分的波动方程叠前逆时偏移方法[J].石油物探,2009,48(5):475-478 Chen K Y.Wave equation pre-stack reverse-time migration method based on high-order finite-difference approach[J].Geophysical Prospecting for Petroleum,2009,48(5):475-478
[3]杨勤勇,段心标.逆时偏移技术发展现状与趋势[J].石油物探,2010,49(1):92-98 Yang Q Y,Duan X B.Development status and trend of reverse time migration[J].Geophysical Prospecting for Petroleum,2010,49(1):92-98
[4]Whitmore N D.Iterative depth migration by backward time propagation[J].Expanded Abstracts of 53rdAnnual Internat SEG Mtg,1983,827-830
[5]McMechan G A.Migration by extrapolation of timedependent boundary values[J].Geophysical Prospecting,1983,31(3):413-420
[6]Loewenthal D,Mufti I R.Reversed time migration in spatial frequency domain[J].Geophysics,1983,48(5):627-635
[7]陈可洋.地震波逆时偏移方法研究综述[J].勘探地球物理进展,2010,33(3):153-159 Chen K Y.Review of seismic reverse time migration methods[J].Progress in Exploration Geophysics,2010,33(3):153-159
[8]Yoon K,Marfurt K J,Starr W.Challenges in re-verse-time migration[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,1057-1060
[9]Dussaud E.Computational strategies for reversetime migration[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,2267-2271
[10]Foltinek D,Eaton D,Mahovsky J,et a1.Industrialscale reverse time migration on GPU hardware[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009,2789-2793
[11]赵磊,王华忠,刘守伟.逆时深度偏移成像方法及其在CPU/GPU 异构平台上的实现[J].岩性油气藏,2010,22(F07):36-41 Zhao L,Wang H Z,Liu S W.Reverse-time depth migration imaging and its application at CPU/GPU platform[J].Lithologic Reservoirs,2010,22(F07):36-41
[12]Araya-Polo M,Rubio F,de la Cruz R,et a1.3Dseismic imaging through reverse-time migration on homogeneous and heterogeneous multi-core processors[J].Journal of Scientific Programming,2009,17(1/2):186-198
[13]Micikevicius P.3Dfinite difference computation on GPUs using CUDA[J].Proceedings of 2ndWorkshop on General Purpose Processing on Graphics Processing Units,2009,79-84
[14]李博,刘红伟,刘国峰,等.地震叠前逆时偏移算法的CPU/GPU实施对策[J].地球物理学报,2010,53(12):2938-2943 Li B,Liu H W,Liu G F,et al.Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J].Chinese Journal of Geophysics,2010,53(12):2938-2943
[15]Symes W W.Reverse time migration with optimal check pointing[J].Geophysics,2007,72(5):SM213-SM221
[16]Villarreal A,Scales J A.Distributed three dimensional finite-difference modeling of wave propagation in acoustic media[J].Computers in Physics,1997,11(4):388-399
[17]李博,刘国峰,刘洪.地震叠前时间偏移的一种图形处理器提速实现方法[J].地球物理学报,2009,52(1):245-252 Li B,Liu G F,Liu H.A method of using GPU to accelerate seismic pre-stack time migration[J].Chinese Journal of Geophysics,2009,52(1):245-252

