起伏地表叠前时间偏移的多级并行优化技术

马召贵 ，赵改善，武港山，孙成龙，亢永敢，杨祥森，曹永生

（1.中国石油化工股份有限公司石油物探技术研究院，江苏南京 211103；2.南京大学软件新技术国家重点实验室，江苏南京 210093）

起伏地表条件下的叠前时间偏移一般先进行静校正处理，将叠前数据校正到一个固定面上再进行固定面偏移［1］。然而，现有的静校正方法都是基于某种理论上的假设来进行的，当这种假设得不到满足时，应该抛弃传统的静校正处理，直接进行叠前偏移处理，并在偏移过程中解决静校正问题［2－3］。叠前时间偏移在生产中发挥着极其重要的作用，但随着勘探工区规模越来越大，以及石油勘探开发对于地震勘探精度的要求越来越高，地震勘探数据量与计算量都有了指数级的增长［4－5］。实践表明，在常规集群系统上进行三维海量地震数据的叠前时间偏移甚费机时，时常使计算成果的产出时间与生产进度需求之间产生严重脱节的局面［6］。

起伏地表Kirchhoff叠前时间偏移具有计算密集和I／O 密集的特点，并行计算方案需要针对算法的运行特征和计算机集群特点综合考虑。李伟等［7］对Kirchhoff积分法偏移的并行实现问题进行了研究，提出了按照分治策略进行叠前数据分割、成像体分块的实现方案。Bhardwaj等［8］利用MPI提供的并行I／O 接口进行了3D 波动方程叠前深度偏移的算法优化，通过I／O 优化，使偏移效率提高了30%。目前地震数据处理普遍采用集群计算机系统，这类系统的CPU 一般为多核结构，单节点的内存大小有限，I／O 带宽有限，网络带宽有限。针对目前主流处理器集群的特点，王华忠等［9］于2010年提出了一种适用于大规模数据体的三维Kirchhoff积分法偏移实现方案，该方案将叠前地震数据按共偏移距道集形式组织，逐个偏移距进行偏移，很大程度上降低了偏移计算对内存的依赖，同时，将成像结果按时间维度进行分块处理，并充分利用本地盘存储数据，很好地解决了大工区大规模数据偏移的内存不足问题，具有很好的工业价值。2012年，王华忠等［10］对以上实现方案进行了优化，提出了一种适用于Kirchhoff积分法叠前深度偏移的并行实现方案，该方案利用OpenMP 多线程技术实现了成像域沿时间切片的任务级并行，结合多线程共享内存的优势提高了多核处理器的使用效率。偏移计算时的数据I／O 会严重影响偏移效率，为了降低I／O 对计算效率的影响，王霖等［11］提出了一种叠前时间偏移并行模式的流水线改进方法，该方法通过建立数据缓冲池实现了I／O与计算的重叠，但是单缓冲池的实现机制使得计算线程增加了一次数据拷贝。

在分布式存储集群环境下如何高效实现三维Kirchhoff叠前时间偏移的大规模并行计算，是一个值得深入研究的课题。其重点是要解决以下问题：①计算进程个数增加带来的通讯开销及其导致的偏移效率快速降低问题；②偏移应用大规模部署或者集中式存储使用密集时的I／O 竞争问题；③大规模数据偏移时的内存资源有限问题；④在没有本地盘的处理器集群上进行偏移模块部署应用的问题。我们在参考前人研究成果的基础上，提出了一种适用于积分法偏移的多级并行优化方案，并对起伏地表叠前时间偏移原始算法进行了优化。

1 起伏地表直接叠前时间偏移方法

Kirchhoff偏移利用边界积分方法近似求解波动方程来实现地震数据的成像，该方法的本质是基于绕射叠加理论的振幅求和过程，并使用加权函数实现振幅校正。我们首先从反假频、弯曲射线高阶旅行时计算以及起伏地表条件下的旅行时校正3个方面对方法原理进行分析。

1.1 局部三角滤波反假频

假频的出现会严重影响Kirchhoff偏移成像结果。叠前地震数据偏移中的假频一般包括数据假频、算子假频和成像假频，在此只讨论算子假频问题。当积分算子的求和轨迹太陡，即跨越相邻道的算子时差超出时间采样率时，就会发生算子假频。Kirchhoff算子反假频可通过孔径控制和算子倾角滤波来实现，但这样会压制陡倾角数据对成像的贡献。也可采用道插值方法进行反假频，但由于现代三维采集的数据体庞大，这种方法代价太昂贵，也太笨拙。我们选择的反假频方法是Lumley等［12］提出的局部三角滤波反假频方法，该方法对假频的压制效果要优于矩形滤波和多带通滤波方法，而且计算效率较高。

地震数据不产生算子假频的准则为

其中，Δt为偏移算子轨迹与相邻两道地震记录相切的两个采样点之间的时差，tk为旅行时，Δρ为相邻两道地震数据的道间隔。根据（1）式可计算出三角形滤波器算子长度，即

每一个成像点的计算都需要对原始输入数据进行N点三角滤波处理，计算效率较低。为提高三角滤波反假频的计算效率，可根据三角滤波器的频率响应特征，在反假频前对地震数据进行一次因果积分和非因果积分处理，在此基础上将长度为N的三角滤波器替换为一个3 点的Laplacian算子，从而在保证反假频处理精度的同时，大大降低计算量。

1.2 优化的弯曲射线高阶旅行时计算

实现叠前时间偏移的一个关键环节是计算地震波走时，所用算法大致可分为3类，即直射线、弯曲射线以及非对称走时计算［13－14］。直射线走时算法基于均匀介质模型，其旅行时计算精度低，而利用射线追踪数值方法计算走时则存在累计误差大、稳定性及计算效率低的问题。为了提高旅行时计算精度，可利用弯曲射线高阶旅行时计算方法，在水平层状介质假设下，不是使用双曲公式计算旅行时，而是将以射线参数表示的旅行时tx和偏移距x的参数方程近似为

（3）式可进一步表示为

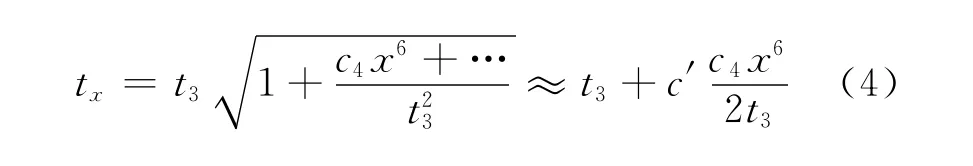
1.3 起伏地表旅行时校正及偏移参考面选择

常规叠前时间偏移一般在统一基准面上进行，在地形变化较剧烈的地区，采用统一基准面校正后再偏移会因静校正的地表一致性假设而引起波场畸变。当近地表速度稳定且高差变化不大时，可采用浮动基准面为偏移参考面，如图1所示。其中红色虚线为当前成像点处对应的局部水平偏移成像基准面。

社会福利政策质量评价方法是指在社会福利政策质量评价中所采用的具体方法，它是实现社会福利政策质量评价的必要手段。从一定角度来看，社会福利政策质量评价方法的选用，决定了社会福利政策质量评价是否成功。近几十年来，随着政策科学的发展，各种新的评价方法不断涌现，大大丰富了社会福利政策质量评价的实践活动。从方法论的角度划分，可以是经验分析的方法，也可以是演绎推理的方法；从事物质和量的角度划分，可以是定性的分析方法，也可以是定量的分析方法或者二者结合使用的分析方法；从评价工具的角度划分，可以是传统的方法，也可以是现代的科学方法④。

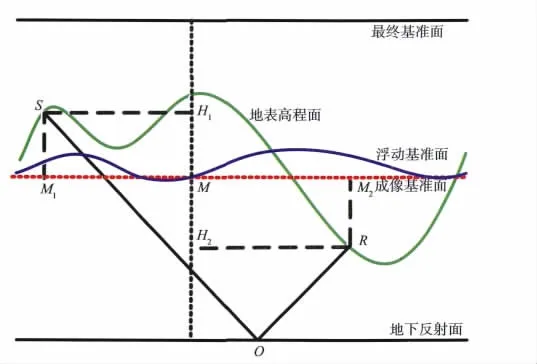
图1 起伏地表走时及成像基准面选择

在浮动基准面作为偏移基准面的条件下，以直射线为例，地震波的双程走时可表示为

其中tS和tR分别表示炮点走时和接收点走时，t0为以成像基准面表示的自激自收时间，hS和hR分别表示炮点高程和接收点高程，hM表示成像基准面高程，v0为替换速度，xS和xR分别为炮点和接收点到共中心点M的水平距离，vs为均方根速度。

2 多级并行方案设计及优化

2.1 原始算法的并行性分析

Kirchhoff叠前时间偏移作为积分类偏移，其算法本身适应于单道数据处理，道与道之间并无依赖，这种特性决定了偏移能以很细的粒度实现高度并行，理论上具有良好的并行加速比。算法对硬件资源的依赖主要体现在：①反假频和对地震道（集）数据进行成像处理占用了绝大部分计算资源；②保存偏移计算过程中的成像道集占用了大部分内存资源；③叠前数据的读取占用了大部分I／O 资源。

图2 Kirchhoff叠前时间偏移原始算法流程

图3 Kirchhoff叠前时间偏移原始算法伪码

图2和图3分别为该算法未采用多级并行优化前的MPI多进程并行实现流程和伪码。该算法实现了对成像体的分块并行处理，每个节点启动的进程数由当前节点的CPU 核数决定，进程间采用对等模式的并行设计，主控进程负责按照道粒度逐道读取输入的CMP道集数据，并将该道数据通过消息传递广播给各个子进程（包括主进程自己），所有进程对该道数据进行反假频滤波，实现对成像体的分块偏移处理。这种并行模式存在木桶效应，即计算速度由最慢的进程决定，同时这种实现模式需要开辟整个成像道集的内存空间，内存消耗很大。断点保护输出的临时文件存储在本地盘，每个进程计算的偏移结果存于集中式存储上，最后由主控进程对每个进程计算的分块成像结果进行组合，形成最终的偏移成像数据体。

该并行方案存在3个方面的问题：

1）只有主控进程进行地震数据的I／O 操作，不能充分发挥高性能并行文件系统的优势，并且主控进程在承担I／O 任务的同时，还承担偏移计算任务，导致进程间负载不均衡。

2）单道读取、单道广播的细粒度实现机制降低了磁盘的I／O 性能，同时，因为单个进程没有数据缓冲功能，导致进程间，特别是节点规模较大时的同步开销很大，影响计算性能。

3）进程间虽然进行了成像体分块处理，但是由于缺乏共享内存的多线程并行机制，在输出成像道集时每个节点（运行着多个进程）的内存消耗仍非常大，难以适应目前大规模工区的处理要求。

表1 原始算法的数据读取及通讯时间

2.2 优化的多级并行框架

三维Kirchhoff叠前时间偏移的实现只有适应计算机集群的体系结构才能获得最佳的计算效率，一个高效的并行计算方案设计及优化必须综合考虑计算平台的计算能力、存储能力、I／O 特点、网络通讯开销以及数据处理规模等多个因素。不同的大规模地震数据叠前偏移处理方案，由于采用的并行计算框架和并行计算策略不同，它们的执行效率和可扩展性也存在较大的差别［10］。

当前计算机集群往往具有节点多、单节点内存容量有限、本地盘小、共享盘大和多I／O 通道等特点，在综合考虑内存使用量、地震数据I／O 量、I／O效率以及偏移成像精度的基础上，以解决原始算法中影响计算效率的3个关键问题为目标，我们设计了如图4所示的一个新的多级并行计算框架。

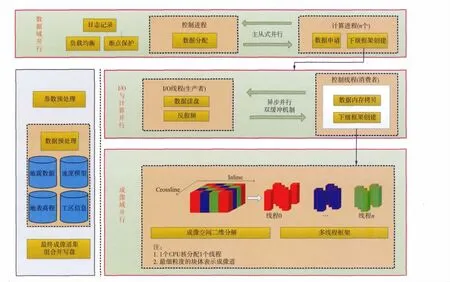
图4 多级并行计算框架

数据域并行是三级并行计算框架的第一级并行，主要实现了共偏移距域的多进程主从式并行，重点解决了负载均衡问题。用于保证进程间负载均衡的技术很多，总体上可分为两类：任务静态分配和任务动态分配。任务静态分配负载均衡策略的优点是易于实现，但往往局限于每个节点计算能力相当的情况，在节点之间计算能力差异比较大时，会出现任务分割很均衡而计算时间不均衡的情况。因此，我们采用主从式多进程并行策略和按需分配的方式实现进程间的动态负载均衡。对主进程来说，首先接收提出任务请求的计算进程ID，然后将下一个要处理的数据块ID 分配给申请进程；对计算进程来说，首先发送自己的进程ID 给主控进程，然后接收申请到的数据块ID，再进行下一步的处理。主控进程只负责控制地震数据的分发而不需要读取地震数据，地震数据的读取由各个计算进程根据申请到的数据块ID 从磁盘读取。由于各个计算进程读取的地震数据不一样，因此当一个偏移距偏移完成后，需要对当前偏移距的偏移结果进行规约操作。

三级并行计算框架的第二级实现了I／O 与计算的异步并行。叠前偏移中面临着突出的I／O 问题，在集群规模大、存储使用密集时，I／O 瓶颈尤其严重。为降低I／O 对计算性能的影响，在考虑到高性能集中式存储往往具有多I／O 通道的情况下，进行了I／O 并行优化。I／O 线程和控制线程的流程及异步通讯方式如图5和图6所示，每个计算进程利用多线程技术产生两个线程，其中一个线程负责数据I／O，另外一个线程负责控制偏移计算。这两个线程可以实现异步并行，将I／O 与计算重叠进行，其中I／O 线程与控制线程通过Pthread信号量实现线程间的通讯及交互控制。为了使两个线程能交替访问同一个缓冲区从而实现缓冲数据的零拷贝，在图5和图6所示的控制逻辑下可以分别在两个线程中设置一个称为Buffer ID 的计数器（两个线程的Buffer ID 初始值必须相同，每循环一次进行一次加1操作），只需要判断该计数器的奇偶性就可以实现缓冲数据的零拷贝。

图5 I／O 线程流程

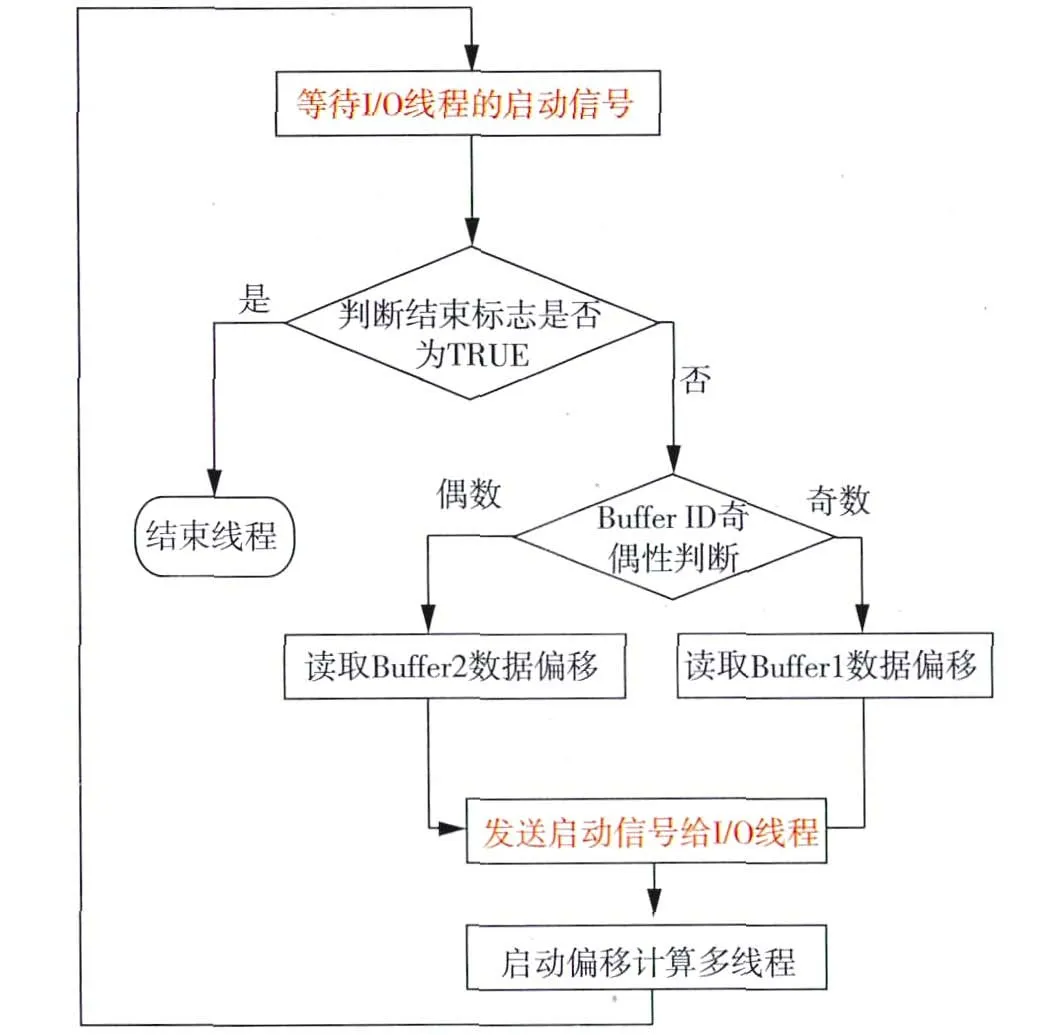
图6 控制线程流程

在输入数据已经读入缓冲区后，利用共享内存实现多线程成像域并行，这是多级并行计算框架的第三级并行。线程间采用静态任务分割方式实现成像体的分块并行，线程间无通讯和依赖关系。由于每一个成像道及其对应的成像点的偏移孔径并不相同，为保证线程间的计算负载均衡，我们采用成像块跳跃划分方式（图4）进行并行处理。通过逐个偏移距顺序进行偏移以及单节点上的多线程共享内存机制，很大程度上降低了大工区偏移处理时的内存瓶颈，但由于每个偏移距道集的成像结果仍然是一个三维成像空间，在工区规模非常大时，单个节点内存可能会出现不够用的情况，这时可以将偏移分成多个作业进行。

3 实际数据测试与分析

我们所有测试所用集群系统环境由34 个SMP节点组成，每个SMP节点有2个CPU（CPU型号为Intel Xeon X5650，主频为2.67GHz）、48GB内存、2个600GB 硬盘，集中存储为Panasas并行集群存储系统。测试数据为某工区实际叠前地震数据，数据大小70GB，共计5 945 570道，记录道长度为6s，时间采样间隔为2ms。偏移计算的参数如下：最小偏移距为0，最大偏移距为12 000m，偏移距间隔为400m，最大偏移孔径为8 000m，成像时间6s，成像采样间隔为2ms。

优化前的算法测试使用了34 个节点，共计397个进程，除了1个控制进程外还包含396个计算进程；优化后的算法测试使用了34个节点，共计34个进程，除了1个控制进程外还包含33×12＝396个计算线程。图7a和图7b分别为算法优化前、后偏移计算时某计算节点的监控结果（暗绿色表示CPU 利用率，亮绿色表示有效浮点计算效率，棕色表示系统占用时间），从图7a不难发现，算法优化前计算节点出现了CPU 有效利用率不足的情况，体现在系统占用时间非常明显（棕红色），而图7b显示算法优化后计算节点的CPU 资源已经得到了充分利用，计算节点未监控到系统占用时间，CPU 的实际性能得到了提高。

图7 算法优化前（a）、后（b）利用Paramon软件监控的某计算节点CPU 利用情况

图8a和图8b分别为算法优化前、后主控节点的网络通讯监控结果，对比可见，算法优化后主控节点的数据发送和数据接收量明显降低。图9a和图9b分别为算法优化前、后某计算节点网络通讯监控结果，算法优化后网络通讯频率明显降低，这是由于优化前的算法只能以道粒度从主控节点获得数据，而优化后的算法通过数据缓冲池以数据块粒度从硬盘直接读取数据。

表2为算法优化前后偏移计算的用时统计结果，多级并行优化技术在提高算法大规模部署能力的同时，使算法运行效率提高了12%左右，这种提高对于大规模集群系统将更加显著。

图10a和图10b分别为算法优化前后L620线的部分偏移剖面，为了方便对比，没有对剖面进行增益处理，从视觉上很难发现图10a和图10b的差异（两个剖面的相似系数为0.998 92）。图10c为图10a和图10b的差异剖面，产生差异的原因有两个，一是算法优化前后采用的工区定义方式不同，从而引入了工区定义精度误差；二是多级并行优化本身引入的精度误差，优化后的算法改变了输入数据的处理顺序，也就改变了成像结果的累加顺序，而浮点数的累加顺序会影响累加结果。

图8 算法优化前（a）、后（b）监控的主控节点网络流量

图9 算法优化前（a）、后（b）监控的某计算节点网络流量

表2 算法优化前、后计算时间

图10 算法优化前（a）、后（b）的偏移剖面及差异剖面（c）

4 结束语

我们分析了起伏地表叠前时间偏移的基本原理及提高偏移精度的特色处理方法，重点针对原始算法实用化过程中影响计算效率和部署规模可扩展性的关键问题，提出了一种适用于积分法偏移处理的多级并行计算架构，并进行了算法优化和大规模测试，验证了三级并行计算架构在计算效率提升和规模可扩充性方面的有效性。

1）利用MPI多进程技术进行偏移距域的数据域并行，消除了成像域并行这一简单并行模式带来的地震数据广播以及成像结果规约等通讯开销，能提高算法大规模部署时的适应能力，大大降低内存资源消耗。在具体实现时，每个计算进程并行进行地震数据的I／O，有效发挥了并行文件系统的优势。

2）基于Pthread多线程技术，采用生产者－消费者模型和双缓冲零拷贝技术实现了数据I／O 与偏移计算的异步并行，降低了I／O 对计算性能的影响。

3）单个计算节点上只启动一个计算进程，进程内利用Pthread多线程技术实现的成像域任务级并行有效降低了偏移计算的总进程数，多线程间共享内存的机制提高了多核处理器的利用效率，同时也大大降低了内存消耗。

［1］朱海波，林伯香，徐兆涛，等.起伏地表叠前时间偏移处理流程及其应用研究［J］.石油物探，2012，51（5）：486－492 Zhu H B，Lin B X，Xu Z T，et al.Prestack time migration scheme from rugged topography and its application［J］.Geophysical Prospecting for Petroleum，2012，51（5）：486－492

［2］郝军，杨瑞娟，吴靖，等.复杂地表地震资料静校正问题的处理［J］.复杂油气藏，2011，4（3）：34－37 Hao J，Yang R J，Wu J，et al.Processing of static correction problems of seismic data in the complex surface［J］.Complex Hydrocarbon Reservoirs，2011，4（3）：34－37

［3］程玖兵，马在田，陶正喜，等.山前带复杂构造成像方法研究［J］.石油地球物理勘探，2006，41（5）：525－529 Cheng J B，Ma Z T，Tao Z X，et al.Imaging study of piedmont complex structures［J］.Oil Geophysical Prospecting，2006，41（5）：525－529

［4］赵改善.我们需要多大和多快的计算机？［J］.勘探地球物理进展，2004，27（1）：22－28 Zhao G S.How big and fast computers can meet our needs？［J］.Progress in Exploration Geophysics，2004，27（1）：22－28

［5］谌艳春，李守济，姚盛，等.高精度三维叠前时间偏移处理技术在四扣地区的应用［J］.石油物探，2005，44（4）：370－373 Chen Y C，Li S J，Yao S，et al.Application of highprecision 3－D pre－stack time migration in Sikou area［J］.Geophysical Prospecting for Petroleum，2005，44（4）：370－373

［6］齐俊宁，朱敏，吴彦伟，等.海量数据叠前时间偏移方法［J］.天然气工业，2008，28（11）：46－48 Qi J N，Zhu M，Wu Y W，et al.The method of prestack time migration in processing enormous data［J］.Natural Gas Industry，2008，28（11）：46－48

［7］李伟，顾乃杰，刘振宽，等.三维叠前Kirchhoff深度偏移软件在并行计算机上的实现技术［J］.计算机工程与应用，2002，20（4）：211－214 Li W，Gu N J，Liu Z K，et al.3－D pre－stack Kirchhoff depth migration and its parallel calculation technique［J］.Computer Engineering and Applications，2002，20（4）：211－214

［8］Bhardwaj D，Yerneni S，Phadke S.Efficient parallel I／O for seismic imaging in a distributed computing environment［J］.Proceedings of 3rdConference and Exposition on Petroleum Geophysics，2000，105－108

［9］王华忠，蔡杰雄，孔祥宁，等.适于大规模数据的三维Kirchhoff积分法体偏移实现方案［J］.地球物理学报，2010，53（7）：1699－1709 Wang H Z，Cai J X，Kong X N，et al.An implementation of Kirchhoff integral prestack migration for large－scale data［J］.Oil Geophysical Prospecting，2010，53（7）：1699－1709

［10］王华忠，刘少勇，孔祥宁，等.大规模三维地震数据Kirchhoff叠前深度偏移及其并行实现［J］.石油地球物理勘探，2012，47（3）：404－410 Wang H Z，Liu S Y，Kong X N，et al.3D Kirchhoff PSDM for large－scale seismic data and its parallel implementation strategy［J］.Oil Geophysical Prospecting，2012，47（3）：404－410

［11］王霖，晏海华.一种叠前时间偏移并行模式的流水线改进方法［J］.微电子学与计算机，2008，25（10）：54－57 Wang L，Yan H H.Method of improving performance of Kirchhoff prestack time migration parallel pattern through pipelining［J］.Microelectronics ＆Computer，2008，25（10）：54－57

［12］Lumley D E，Claerbout J F，Bevc D.Anti－aliased Kirchhoff 3－D migration［J］.Expanded Abstracts of 64thAnnual Internat SEG Mtg，1994，1282－1285

［13］刘洪，刘国锋，李博，等.基于横向导数的走时计算方法及其在叠前时间偏移中的应用［J］.石油物探，2009，48（1）：3－10 Liu H，Liu G F，Li B，et al.The travel time calculation method via lateral derivative of velocity and its application in pre－stack time migration［J］.Geophysical Prospecting for Petroleum，2009，48（1）：3－10

［14］朱海波，方伍宝，孔祥宁，等.扩展的横向变速叠前时间偏移技术［J］.石油物探，2009，48（2）：153－156 Zhu H B，Fang W B，Kong X N，et al.Extended prestack time migration for laterally variable velocity［J］.Geophysical Prospecting for Petroleum，2009，48（2）：153－156