基于动力吸振器的空间桁架多自由度振动抑制

杨 恺 崔 龙 黄 海

(北京航空航天大学 宇航学院，北京100191)

航天器上使用的大型轻质柔性桁架结构具有刚度低，阻尼小的特点，受扰后引起的振动难以衰减，对航天器姿态精确保持和结构寿命造成了不利影响.国内外学者提出在柔性结构中嵌入如压电陶瓷、磁致伸缩材料等智能结构的方法进行振动的主动控制［1］.然而，对于类似盘压杆等变形展开式桁架结构以及空间站使用的大型桁架结构难以通过植入上述主动元件的方法进行振动抑制，限制了这类结构的应用.

采用动力吸振器(DVA，Dynamic Vibration Absorber)能有效解决上述结构的振动抑制问题.DVA的抑振原理为:在结构上附加弹簧质量块系统，当结构振动时，引起该附加系统质量块的振动，使其产生对结构的反向作用力，抑制结构的振动［2］.

采用 DVA进行结构的振动控制，无需将DVA植入被控结构中，因此适用于变形展开式结构的振动控制.相对其他减震装置而言，DVA具有高效可靠和低维护成本的优点［3］，在振动控制领域已有广泛的应用［4］.

由于主动DVA具有更宽的控制带宽以及更好的控制效果，因此，针对主动DVA控制方法的研究也受到了广泛关注，例如，文献［5］提出了基于扩张状态观测器原理的DVA主动振动控制方法，并针对一个桁架模型进行了单自由度振动控制的仿真验证;文献［6］将DVA质量块的位移速度信号作为反馈信号，提出了一种最优振动控制方法，并针对柔性梁结构进行了振动控制的仿真验证;文献［7］将DVA质量块与结构的相对位移、速度增加到反馈控制环节中，改进了传统DVA速度反馈控制的鲁棒性.

上述控制方法均需要对结构的动力学模型进行精确建模，其控制性能和鲁棒性受到结构参数的影响.然而空间桁架结构的振动为多自由度，其结构模型不仅复杂，而且存在诸多的不确定性，甚至在复杂的空间环境下结构参数会发生改变，这些特性导致难以利用精确的空间结构动力学模型设计控制器.因此如何在不需要建立精确动力学模型的情况下，利用多DVA实现对这类复杂结构的多自由度主动振动控制是亟待解决的问题.

本文提出了一种基于DVA的桁架多自由度自适应振动控制方法，以解决复杂桁架系统的多自由度振动问题.该控制方法在(ADC，Adaptive Disturbance Canceller)算法［8］的基础上提出，可在被控对象模型未知的情况下通过自适应控制算法实现对桁架多自由度多频率的振动抑制.首先介绍了单自由度DVA的振动控制原理，在此基础上，阐述了基于DVA的桁架多自由度振动控制策略，然后仿真验证了单个DVA对多频扰动的自适应抑制能力，最后建立了DVA-三棱柱桁架实验装置，进行了三自由度振动主动控制实验，验证了方法的有效性.

1 基于DVA的桁架振动抑制原理

1.1 单自由度DVA振动控制原理

本文采用电磁式DVA进行振动控制，将其安装在一个单自由度柔性结构上，形成如图1所示的单自由度DVA振动控制系统.该DVA采用磁铁为动子，线圈为定子的作动方式，以充分利用磁铁的自身质量，增加DVA的振动控制效果.

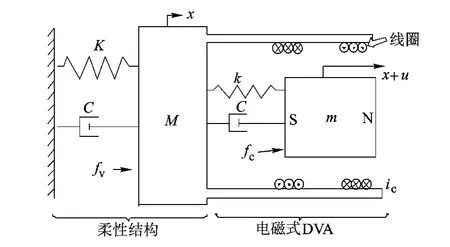
图1 电磁式DVA单自由度振动控制原理

如图1所示，DVA磁铁质量为m，弹簧刚度为k，电磁阻尼系数为c.当线圈通入控制电流ic时，在磁场作用下产生主动力fc推动磁铁，从而产生反作用力P:

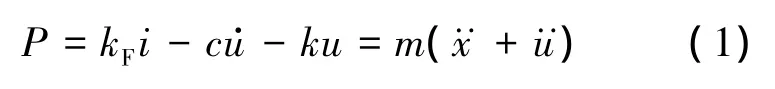
式中，x和u分别为被控结构的振动位移以DVA磁铁相对被控结构的位移;kF为DVA的电流-力常数，其与线圈匝数和磁场强度有关.

则被控结构满足的动力学方程为

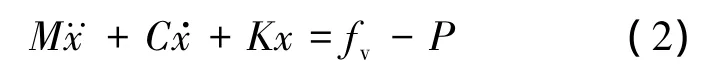
式中，M，C和K分别为被控结构的质量、阻尼和刚度;fv为干扰力.

当线圈无控制电流时，通过调整合适的DVA弹簧刚度与阻尼可被动抑制结构固有频率附近的振动［2］.

1.2 DVA-桁架多自由度振动控制策略

将多个单自由度DVA安装在桁架顶部，可实现对桁架多自由度的振动抑制.如图2所示，以一个安装在航天器本体上的三棱柱桁架为研究对象，该桁架共m层，桁架每层为等边三角形构型，外接圆半径为R，其顶部为一个平板(视为刚体).坐标系Oxyz固联在桁架底部，其原点O在桁架底部三角形的形心处，Ox与图中的1，2点的连线平行，Oz竖直向上.桁架底部受到持续力向量fv的干扰，引起振动.桁架顶部的主要振动形式为沿Ox，Oy的平动振动Vx，Vy和绕Oz的扭转振动φ.为抑制上述3种振动，将3个DVA分别安装在图中的1，2，3顶点处，且每个DVA的轴向与顶点对边平行，则DVA产生的反作用力Pi，i=1，2，3的方向分别与顶点对边平行.

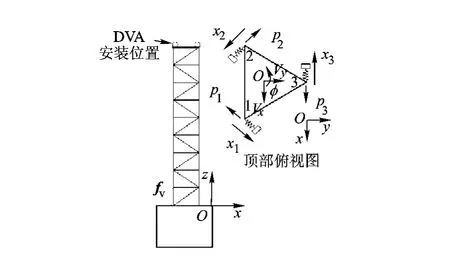
图2 DVA-桁架三自由度振动控制模型

由图2所示的几何关系可知，桁架顶部1，2，3节点沿各DVA轴向方向的振动位移分别为 x1，x2，x3，其与 Vx，Vy和 φ 一一对应，只要抑制 x1，x2和x3，即能抑制桁架顶部的振动.

该桁架满足的动力学方程为

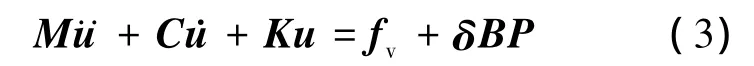
式中，M，C，K分别为桁架质量、阻尼和刚度矩阵;u为各节点振动位移组成的向量;fv为外扰动力向量;B 为 DVA 反作用力向量 P=［P1，P2，P3］T投影至Oxyz的转移矩阵，且BTB为3×3维单位阵;δT=［0…|I］，其中，I为单位矩阵，表示对应的节点位置.

设该桁架顶部平动、扭转振动对应的模态矩阵为ψ，则方程(3)在该模态坐标下为

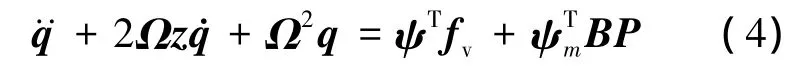
式中，2Ωz，Ω2分别为模态阻尼和模态刚度矩阵，且为对角阵;ψTm为ψTδ不全为零的分块矩阵.由图2几何关系可知，x=-BTψmq.采用单输入-单输出(SISO)控制，即根据式(1)所示，分别控制各DVA 使其产生 P1，P2和 P3，实现对 x1，x2和 x3的抑制.此种控制策略下，桁架受到的总干扰由动力学耦合带来的干扰以及扰动力带来的干扰组成.

2 自适应振动控制算法

柔性桁架受到的扰动主要来源于反作用飞轮、陀螺等造成的扰动.这类扰动往往为单频或多频扰动，当其频率接近桁架共振频率会引起桁架的剧烈振动.针对这类振动工况，主动控制采用ADC算法.该算法利用LMS(Least Mean Square)自适应滤波原理抑制与基底信号频率相同的简谐扰动［8］.为能够抑制具有多个频率的混合干扰，需增加相应的基底信号对.单个 DVA的多频ADC振动控制原理如图3所示.图中，设多频干扰力fv引起结构振动，外扰力与系统耦合项引起的总扰动位移Di表示为

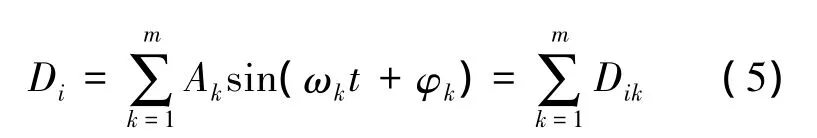
式中，Ak，ωk和 φk分别为第 k个干扰的振幅、频率和相位，其中，Ak，φk时变.

ak和bk分别是频率为ωk的基底信号的比例系数.各基底信号对乘以各自比例系数后，相加产生控制电流信号，再经过DVA-桁架环节，使i点产生的控制位移为

式中，αk和βk分别为DVA-桁架系统在频率为ωk处的幅值增益和相位延迟;n为采样时刻.通过调整系数 ak，bk，使 yik的幅值趋于 Dik，相位趋于 βk+π，从而使xi→0.系数通过LMS滤波器进行实时迭代求解，迭代过程如下:

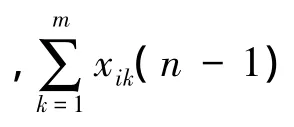
针对图1的单自由度DVA振动控制系统，进行多频ADC算法的仿真验证，仿真参数如下:被控结构 M=1 kg，C=0.5(N·s)/m，固有频率7 Hz，DVA 固 有频 率 7 Hz，m=0.02 kg，c=0.15(N·s)/m，kF=1.DVA质量与主结构质量之比为0.02.扰动力是幅值为1 N，7 Hz，10 Hz组成的多频干扰.多频 ADC基底信号对的频率为7 Hz，10 Hz，算法收敛系 数分 别 取 0.001与0.005.传感器噪声为功率10-5白噪声.频域结果见图4.

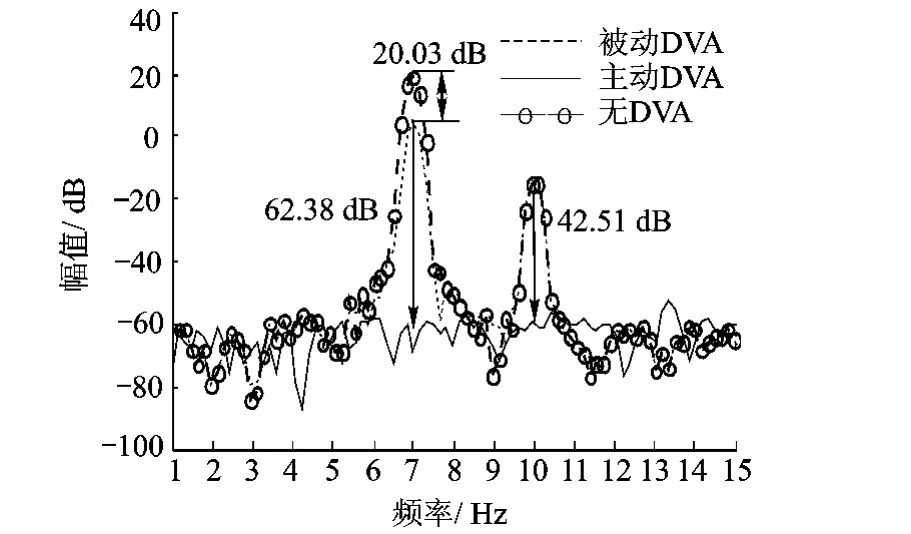
图4 单自由度DVA的多频主动控制仿真结果

仿真结果显示，被动DVA仅对7 Hz(共振频率)振动分量抑制了20.03 dB，而采用多频ADC算法的主动DVA对7 Hz和10 Hz振动分量抑制效果分别提高了62.38 dB，42.51 dB，主动控制最大电流为0.694 4 A，结果表明主动DVA较被动DVA具有更宽的控制带宽和更良好的抑振效果.

3 DVA-桁架多自由度振动控制实验

针对一个三棱柱桁架，采用多频ADC算法进行了基于多个DVA的三自由度主动振动控制实验，以验证多自由度振动控制效果.

3.1 实验系统

搭建了如图5所示的实验系统.该实验系统由三棱柱桁架、压电作动器(模拟干扰源)、3个电磁式 DVA(1，2，3)、加速度计、电荷放大器、dSPACE控制器和功率放大器组成.

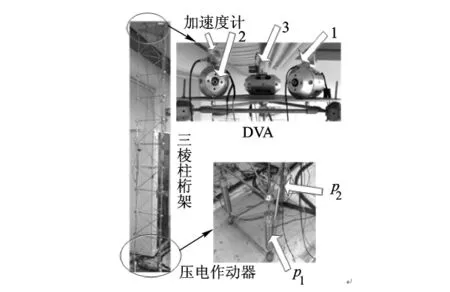
图5 DVA-桁架三自由度振动控制实验系统

其中，三棱柱桁架一阶、二阶共振频率为7 Hz，振型为沿两个水平方向.底部的两根压电作动器(P1，P2)用于产生对桁架的干扰力，以模拟外部干扰.用上述两根压电作动器同时产生相位差60°的干扰力，以使桁架产生明显的扭转振动.DVA的磁铁质量为0.23 kg，外壳质量为0.25 kg，电流-力系数kF为1.23 N/A.DVA布局方向与图2一致.各DVA外壳上的加速度计(灵敏度500 mV/g)，测量桁架顶部节点沿DVA轴向的振动加速度，经电荷放大器双积分得到振动位移.实验采用dSPACE1103 PPC作为控制器，该控制器输出控制电压，通过功率放大器以0.1的比例转化为DVA的控制电流.当桁架振动，加速度计采集振动信号，经dSPACE控制器计算并输出控制信号，控制DVA，实现振动抑制.

3.2 实验结果

分别进行了对7 Hz的单频干扰以及7 Hz，10 Hz多频干扰的振动控制实验，实验参数如下:压电电压幅值为4 V，对应7 Hz基底信号的ADC算法收敛系数为0.001;对应10Hz基底信号的收敛系数为0.005.采样频率为1 kHz.实验结果如图6所示.

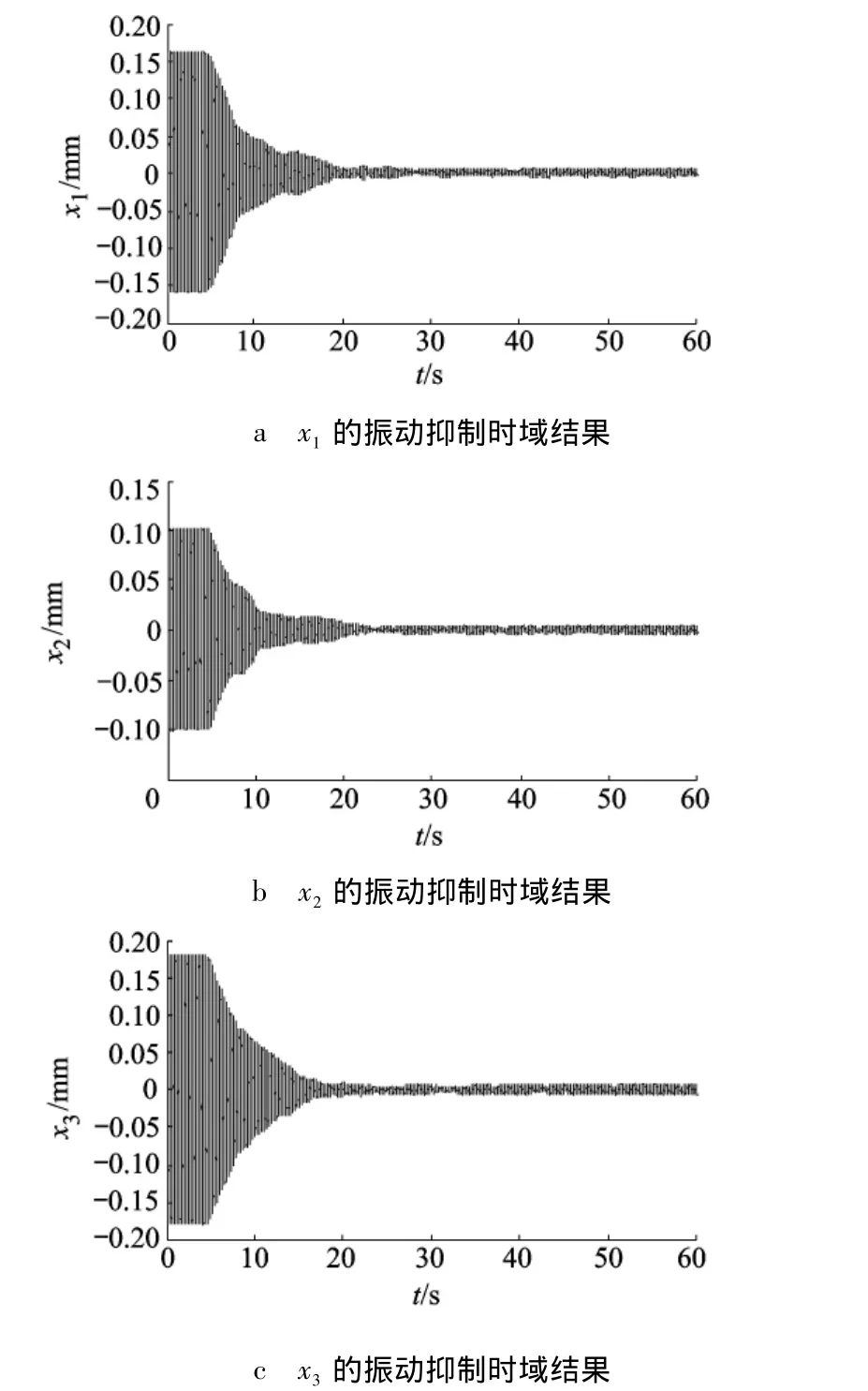
图6 7Hz干扰下的振动抑制实验结果

1)对7 Hz干扰的控制实验.实验结果如图6显示，当第5秒开启主动控制后，振幅分别由最初的0.1623 mm，0.1029 mm和0.1805 mm分别衰减至0.0079 mm，0.0066 mm和0.0090 mm，衰减幅度分别为95.13%，93.59%和95.01%，对7 Hz单频干扰的抑制效果分别提高了26.25 dB，23.82 dB和 26.04 dB，最大控制电流分别为0.146 A，0.102 A 和0.180 A.

2)对7 Hz，10 Hz多频干扰的控制实验.实验结果如图7所示，当第5秒开启主动控制后，最大振幅分别由最初的 0.228 3 mm，0.1302 mm和0.2492 mm衰减至 0.013 1 mm，0.0110 mm和0.0164 mm，衰减分别为 94.26%，91.55%和93.42%.频域分析结果显示，对7 Hz分量的抑制效果分别为36.79 dB，33.12 dB以及34.72 dB，对10 Hz分量的抑制效果分别为20.97 dB，19.46 dB以及22.69 dB，幅值均衰减至传感器噪声级别.最大控制电流分别为0.338 A，0.284 A和0.400 A.

图7 7 Hz，10 Hz干扰下的振动抑制实验结果

4 结论

通过本文的研究工作，得到以下结论:

1)DVA安装在结构的表面，避免了对结构的改造，可应用于盘压杆、充气结构以及大型空间桁架结构等难以植入主动元件的空间可展开机构和结构的振动控制.

2)本文采用的多频ADC自适应算法，可实现在被控对象模型未知的情况下进行DVA的主动振动控制，仿真结果显示，该算法对多频干扰具有良好的抑制能力，相对被动DVA，各频率分量抑制效果分别提高了62.38 dB和42.51 dB.

3)由桁架三自由度振动控制实验结果可知，采用多频ADC算法进行SISO主动振动控制后，对单频振动的各自由度抑制效果分别为95.13%，93.59%和95.01%，对多频振动的各自由度抑制效果分别为94.26%，91.55%和93.42%.控制方法简单有效，便于工程应用.

References)

［1］ Chopra I.Review of state of art of smart structures and integrated systems［J］.AIAA Journal，2002，40(11):2145-2187

［2］ Ormondroyd J，Hartog D.The theory of the dynamic vibration absorber［J］.ASME JournalofApplied Mechanics，1928(49):A9-A22

［3］ Nagarajaiah S.Adaptive passive，semi-active，smart tuned mass dampers:identification and control using empirical mode decomposition，Hilbert transform，and short-term Fourier transform［J］.Structure Control and Health Monitoring，2009，16(7/8):800-841

［4］ Wright R I，Kidner M R F.Vibration absorbers:a review of application in interior noise control of propeller aircraft［J］.Journal of Vibration and Control，2004，10(8):1221-1237

［5］ Hillis A J.Active motion control of fixed offshore platforms using an extended state observer［J］.Proceedings of the Institution of Mechanical Engineers，Part I:Journal of Systems and Control Engineering，2010，224(1):53-63

［6］ Chatterjee S.Optimal active absorber with internal state feedback for controlling resonant and transient vibration［J］.Journal of Sound And Vibration，2010，329(26):5397-5414

［7］ Utsumi M.Active stabilization of a hybrid vibration absorber subject to subjected to velocity feedback control［J］.AIAA Journal，2007，45(4):786-792

［8］ Taranti C G R.A computationally efficient algorithm for disturbance cancellation to meet the requirements for optical payloads in satellites［D］.California:Montery Ca Dept of Electrical and Computer Engineering，Naval Postgraduate School，2001