细水雾灭火的突变分析

杨立军 佟明羲 赵建波

(北京航空航天大学 宇航学院，北京100191)

细水雾由于高效、环保、获得方便等优点在工程技术领域得到广泛的应用［1-2］.细水雾灭火是一个非常复杂的物理、化学过程，这一过程涉及到换热、流动、燃烧等环节.对细水雾灭火机理的探索，通常是基于流体力学、燃烧学等理论，采用数值模拟手段对细水雾与火焰相互作用过程进行模拟［3-5］，但由于细水雾灭火过程的复杂性，至今还无法做到准确模拟.此外，由于细水雾作用下的火焰由燃烧到熄灭的过程转变是一个化学反应中断的过程，采用流体力学、热力学中连续函数所描述的控制方程组只能反映熄灭前的细水雾与火焰相互作用过程的参数的变化情况，无法描述由一个稳定态(燃烧)到另一个稳定态(熄灭)的变化过程，因此也无法得到细水雾灭火的火焰熄灭判据(火焰熄灭边界)，火焰熄灭边界只能通过大量的实验得到.然而，细水雾扑灭火灾属于破坏性实验，每一次实体实验的费用都非常昂贵.谢苗诺夫［6］的着火理论只能针对简单闭口系统的预混燃气进行理论分析，无法利用该理论得到细水雾的灭火判据.因此，迫切需要采用新的理论探索细水雾灭火机理.突变理论［7-9］是研究外部参数发生连续变化引起系统状态发生突变的一种数学方法，本文尝试应用突变理论建立细水雾灭火过程数学模型，得到火焰熄灭边界及火焰临界熄灭温度，为细水雾灭火的工程应用提供理论指导.

1 突变模型的建立

1.1 势函数的导出

从细水雾灭火过程中的各能量转化关系着手［10］，在不考虑热辐射的情况下，建立该过程的能量守恒方程:

其中，G为燃气流量;Cp为燃气定压比热容;T为火焰温度;t为时间;ρ为空气密度;V为参与燃烧的空气体积;fox为氧浓度;Qox为单位质量氧气参与燃烧放热量;k为反应式指前因子;E为反应活化能;R为气体常数;A为火焰面积;h为传热系数;T0为环境温度;mevap为细水雾蒸发速率;L为细水雾气化潜热;C为细水雾比热容.

定义下列物理量［10］:

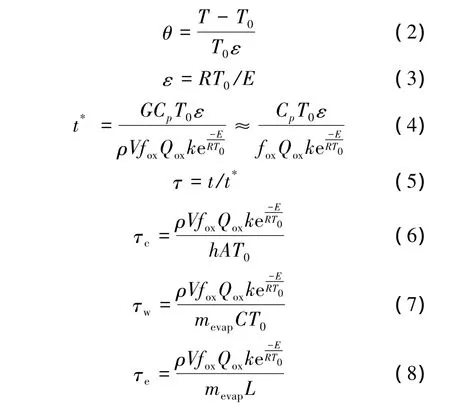
方程左边项做如下变换:

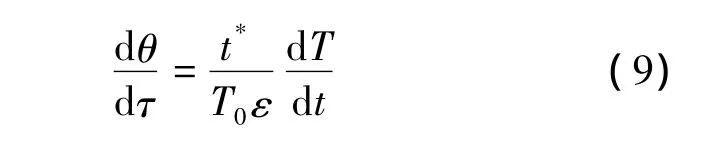
将式(2)～式(9)代入式(1)，整理有

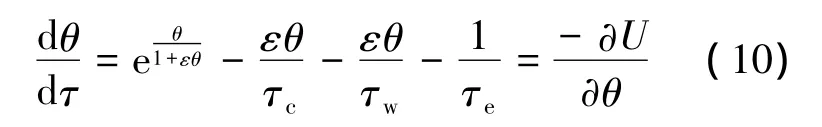
作二次多项式近似如下［10］:

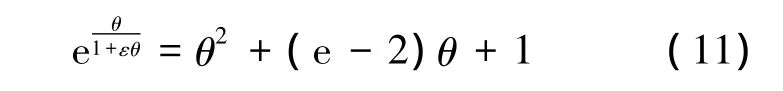
将式(11)代入式(10)并积分，有

根据突变理论可知，其类型为折迭突变.该折迭突变的平衡曲线即火焰熄灭边界为

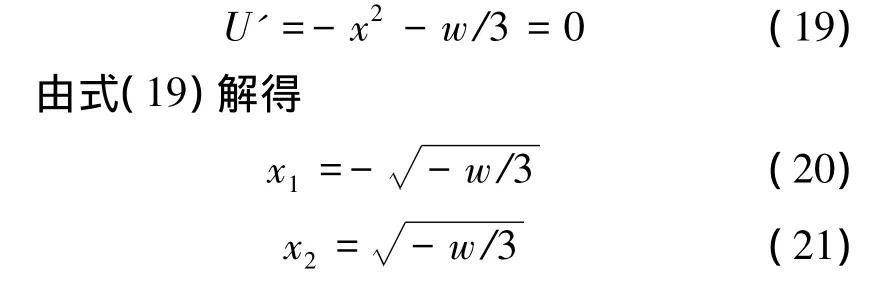
由于灭火时雾滴的无量纲蒸发时间τe≪1，故由式(13)有 a1＜0，由式(17)有 w＜0.w＜0 时势函数的趋势如图1所示.在区域内，随着无量纲温度x的降低，势函数单调下降，相点趋向x1处.此时火焰温度较低，得以熄灭.在 x＞区域内，随着无量纲温度x的降低，势函数单调增加，此时火焰持续燃烧.因此，火焰的熄灭是由于系统发生突变引起的.突变的临界点为，熄灭区域为

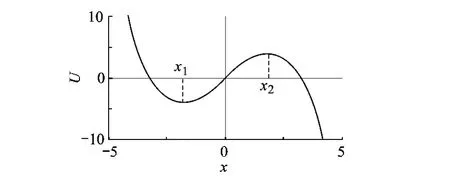
图1 势函数(w＜0)

1.2 火焰临界熄灭温度的导出

将式(13)、式(14)、式(17)代入式(21)，有

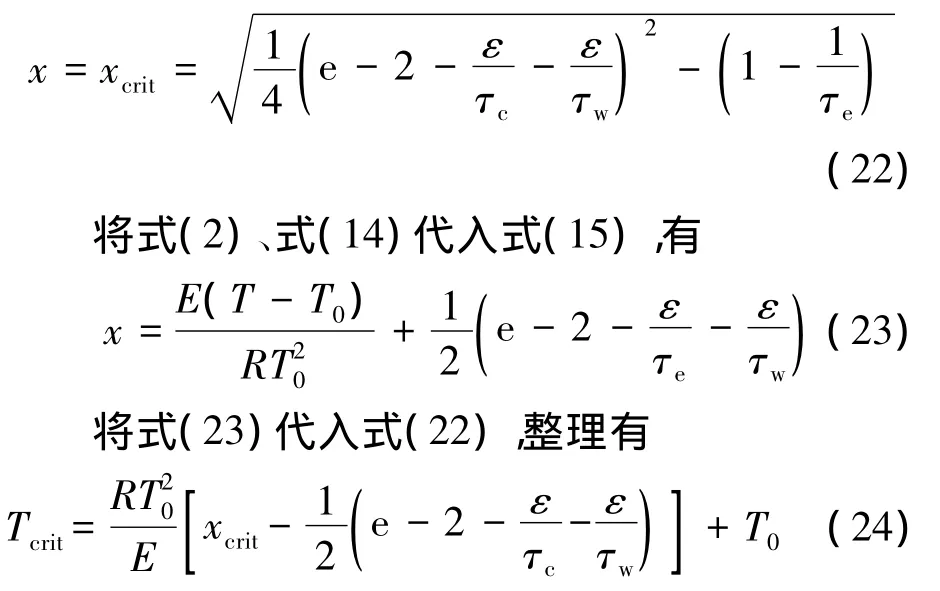
当火焰温度低于火焰临界熄灭温度Tcrit时才有可能会熄灭.

2 细水雾灭火实验

2.1 实验系统及测试仪器

本文研究在北京航空航天大学特种装备细水雾灭火实验室进行，实验系统主要由高压供水系统、细水雾生成系统、吊顶高度调节系统和测试系统组成.其中，高压供水系统由贮水罐、柱塞泵、管路、过滤器、阀门等组成，细水雾生成系统由不同间距的喷头组成，高度调节系统由移动吊顶、滑轮、钢丝绳、导柱、定位销等组成，测试系统由热电偶、流量计、氧浓度仪、数据采集系统等组成.

灭火房间长4.6 m，宽3.3 m，高4 m，吊顶可在2.0～3.5 m范围内任意调节.进行单喷头实验时，油盘放置在喷头的正下方.进行四喷头实验时，喷头布置间距为1.5 m，油盘中心和四喷头对角线交点重合.燃料为正庚烷.火焰温度测量采用5根热电偶组成的热电偶树，氧浓度测量采用西门子Oxymat6氧气分析仪.具体灭火房间布置及温度和氧浓度采样点位置见文献［11］.

2.2 实验内容及方案

实验准备完成后，打开房间门，开启数据采集系统，点燃油盘，经过一段预燃时间后，细水雾开始喷出灭火.在水雾喷射时刻，关闭房间门，当火焰被扑灭时，停止喷射细水雾，并同时打开房间门，测试系统再继续工作一段时间后关闭.将油盘内的正庚烷再次点燃，能够点燃的视为灭火成功.实验方案见表1和表2.其中W为火焰功率，H为吊顶高度，P为系统压力，t0为预燃时间.灭火实验进行过程中，典型火焰温度变化曲线见图2，典型氧浓度变化曲线见图3.

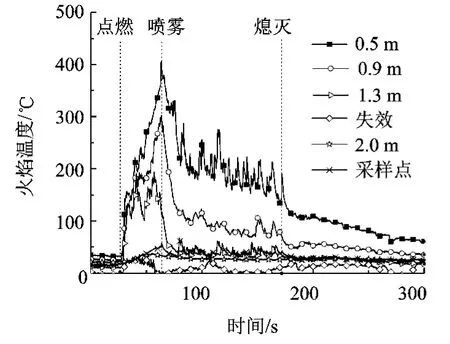
图2 温度随时间变化(单喷头，W=0.1 MW)

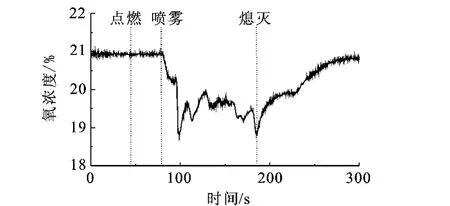
图3 氧浓度随时间变化(单喷头，W=0.1 MW)

2.3 实验测量结果

按照表1和表2中列出的工况，共计进行112次灭火实验，实验均取得灭火成功.每次实验工况下测得的部分火焰熄灭温度Tb与fox见表3.

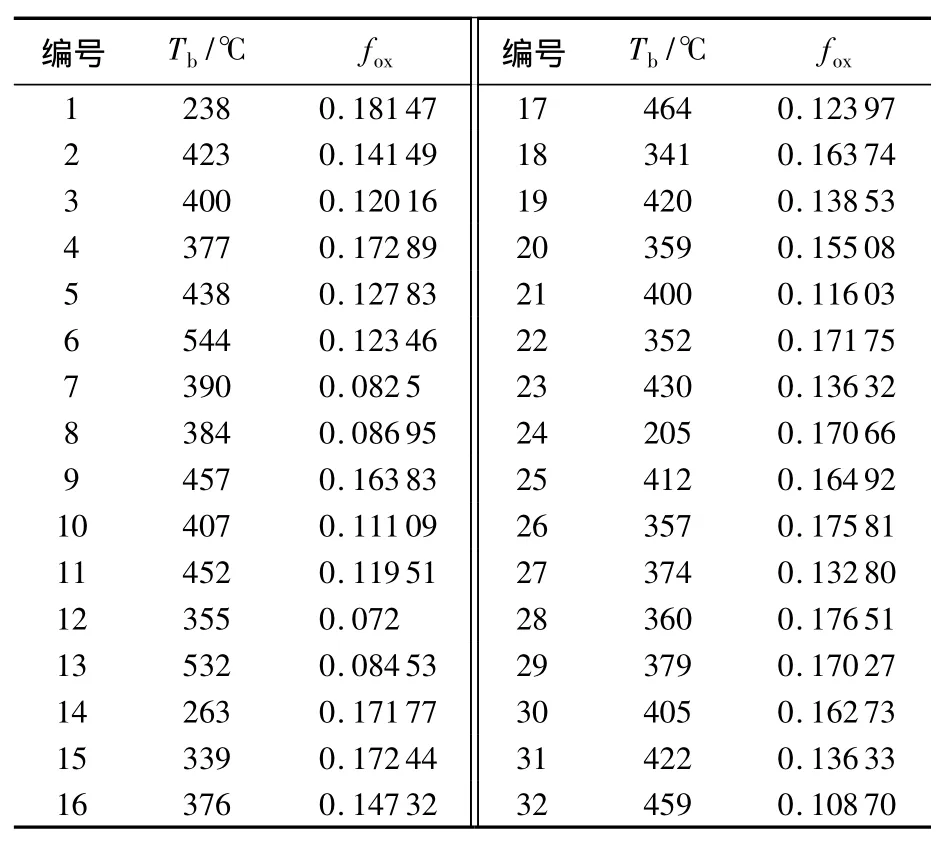
表3 细水雾灭火实验数据

3 实验验证

通过在自行搭建的细水雾灭火系统上进行实验，测得一系列成功灭火的实验数据.将表3中每一个工况下的火焰熄灭温度代入式(2)，氧浓度分别代入式(6)～式(8)，并结合正庚烷及细水雾物性参数算得式(2)～式(3)、式(6)～式(8)的值.将求得的 τc，τw，τe及 ε 代入式(13)和式(14)求得 a1，a2，进而由式(15)、式(17)得到对应于每一实验点数据的x和w数值.

现将无量纲化处理的实验点数据与理论分析中得到的火焰熄灭边界作图进行对比，其中火焰熄灭边界曲线由式(19)画出，其内部为熄灭区，外部为燃烧区，对比结果见图4.由于火焰熄灭是一个不连续的突变过程，外界干扰控制变量(如低温、气流流动等)的引入会引起火焰熄灭温度的剧烈变化，导致相同实验条件下测得的火焰熄灭温度相差较大，甚至发生突变而越过理论熄灭边界.如图4所示，处于熄灭边界附近的6个实验点发生跳跃而到达边界外部，其余106个成功灭火的实验点均落在熄灭区内，从而验证了理论分析中得到的火焰熄灭边界的正确性.

图4 熄灭边界的验证

由式(24)可知，无量纲温度x与火焰临界熄灭温度存在正相关的关系.由图5可知，在实验过程中随着火焰功率的增加，火焰的熄灭温度也相应增加，对于较大功率的火焰只要火焰温度刚刚小于临界火焰熄灭温度即可熄灭.火焰熄灭是吸热与稀释氧浓度的共同作用.当火焰功率较大时，细水雾蒸发速率较快，氧浓度能够被稀释到很低的水平.此时细水雾灭火的机理主要是氧气稀释.而当火焰功率较低时，氧气浓度较高，氧气稀释在灭火中所起的作用有限，火焰熄灭的主要机理是吸热.吸热过程相比于稀释氧浓度较为缓慢，因此灭火时间长，灭火时火焰温度低.由此可知，在扑灭火灾时，应以减小氧浓度为主要目标，才能容易在较高的温度下实现灭火.

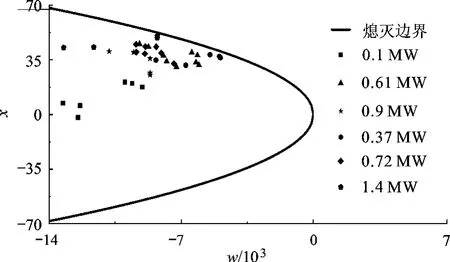
图5 熄灭温度随火焰功率的变化

4 结论

细水雾灭火是一个受物理和化学因素影响的复杂过程.实验工况处于火焰熄灭边界内时可能实现成功灭火.火焰临界熄灭温度与细水雾和燃气性质、环境温度及氧浓度等因素有关.火焰熄灭温度受吸热及氧浓度的影响较大，且吸热过程相对氧浓度稀释作用较为缓慢.

References)

［1］ Ni X M，Chow W K.Performance evaluation of water mist with bromofluoropropene in suppressing gasoline pool fires［J］.Applied Thermal Engineering，2011，31(17/18):3864-3870

［2］ Lechene S，Boulet P.Water mist and radiation interactions:application to a water curtain used as a radioactive shield［J］.Numerical Heat Transfer Part A:Applications，2010，57(8):537-553

［3］ Nmira F，Consalvi J L，Kaiss A.A numerical study of water mist mitigation of tunnel fires［J］.Fire Safety Journal，2009，44(2):198-211

［4］ Trelles J，Mawhinney J R.CFD Investigation of large scale pallet stack fires in tunnels protected by water mist systems［J］.Journal of Fire Protection Engineering，2010，20(3):149-198

［5］ Ferng Y M，Liu C H.Numerically investigating fire suppression mechanisms for the water mist with various droplet sizes through FDS code［J］.Nuclear Engineering and Design，2011，241(8):3142-3148

［6］傅维标，卫景彬.燃烧物理学基础［M］.北京:机械工业出版社，1981:51-62 Fu Weibiao，Wei Jingbin.Combustion physics［M］.Beijing:China Machine Press，1981:51-62(in Chinese)

［7］ Saunders P T.An introduction to catastrophe theory［M］.Cambridge:Cambridge University Press，1980

［8］ Bertola V，Cafaro E.Deterministic-stochastic approach to compartment fire modeling［J］.Proceedings of The Royal Society AMathematical Physical and Engineering Sciences，2009，465(2104):1029-1041

［9］ Carbo D R，Besalu E.Construction of coherent nano quantitative structure-properties relationships(nano-QSPR)models and catastrophe theory ［J］.SAR and QSAR in Environmental Research，2011，22(7/8):661-665

［10］翁文国，范维澄.突变理论应用于腔室火灾中的回燃现象［J］.数学物理学报，2002，22A(4):564-570 Weng Wenguo，Fan Weicheng.Study on catastrophe behavior of backdraft in building fires ［J］.Acta Mathematica Scientia，2002，22A(4):564-570(in Chinese)

［11］杨立军，王向东，廖圣洁，等.油面距油盘沿口高度对细水雾灭火效果的影响 ［J］.北京航空航天大学学报，2008，34(10):1139-1142 Yang Lijing，Wang Xiangdong，Liao Shengjie，et al.Effect of heptanes-to-brim of pool distance on water mist fire suppression［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(10):1139-1142(in Chinese)