旋转大气下火星探测器轨道捕获

吕 敬 张明明

(北京航空航天大学 航空科学与工程学院，北京100191)

龚胜平

(清华大学 航天航空学院，北京100084)

从20世纪60年代开始，前苏联和美国多次成功发射了火星探测飞行器，积累了丰富的深空探测经验.而我国的火星探测轨道技术尚处于发展研究阶段，初步提出了未来十几年内深空探测工程研究.随着探月工程的顺利进行，火星探测也将提上研究日程.

在进行火星探测任务时，火星探测器使命轨道捕获研究是探测轨道设计及任务规划的重要部分，而大气辅助捕获又可细分为多次穿越和一次穿越两种方式，由于一次穿越大气需要较为精确的入射角以及消耗较大的能量，工程实践上多采用多次穿越大气的方式［1-5］，因此本文将采用多次捕获的手段进行相应的大气辅助捕获研究.现有的火星探测轨道捕获都是基于火星大气为静止状态得出的研究结果［1-6］，事实上大气并非处于绝对静止状态，而是有旋转的.

研究地球外部旋转大气对地球卫星轨道的影响时，认为大气由地球“带动”，随地球自转而旋转，其旋转角速度等于地球的自转角速度［7-9］，在离地球较近的位置，旋转大气对探测器的影响比较明显［10］.

本文在研究火星旋转大气环境对卫星轨道的影响时，采用与研究地球旋转大气时相似的假设:火星外部旋转大气的角速度跟火星的自转角速度相同.本文采用多次穿越的方式进行轨道捕获研究，对两种大气模型下轨道参数、任务耗时以及探测器所承受的热量和过载情况进行对比分析，得出结论:当目标轨道近火点较低时，需要考虑旋转大气的影响.

1 火星探测器的动力学模型

1.1 探测器飞行动力学方程

建立火星惯性坐标系Oxyz，坐标原点O位于火星质心，Oxy坐标面为火星赤道面，x轴的方向指向近火点方向，z轴为火星的自转方向，y轴与x和z轴构成右手系.探测器进入火星大气后，其探测器动力学矢量方程可以表示为如下形式:

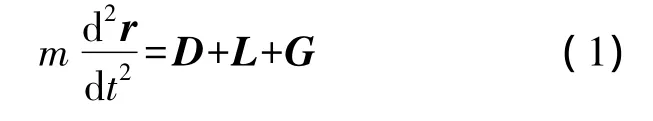
式中，r为探测器的位置矢量;D，L，G分别为作用在探测器上的气动阻力矢量、升力矢量以及重力矢量.探测器受到的阻力加速度、升力加速度［4］以及重力加速度分别为

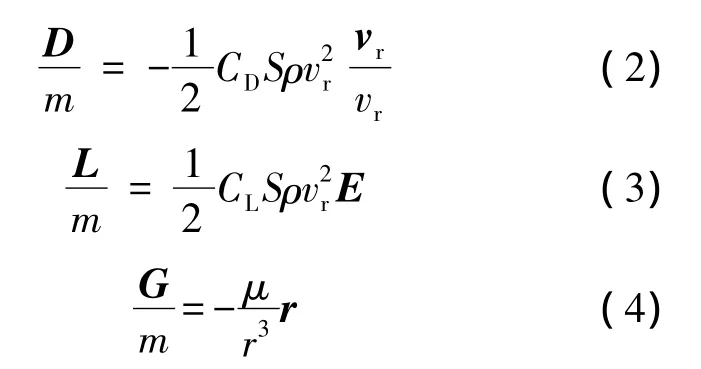
式中，火星的大气密度 ρ= ρ0e-0.000165H［1］，其中 H为探测器所处的轨道高度;CL，CD分别表示升力系数和阻力系数;S为探测器面积;m为探测器质量;vr为探测器相对大气的飞行速度矢量，定义为vr=v-vg，v为探测器在火心惯性坐标系的飞行速度矢量，vg为大气在火心惯性坐标系的速度矢量，且vg=ω×r，其中ω为火星自转角速度矢量;μ为火星的引力系数.另外式(3)中E定义为

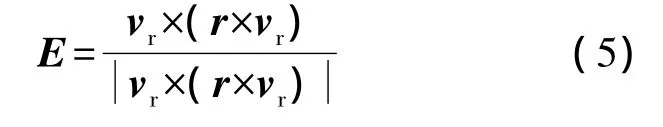
将式(2)～式(5)代入式(1)可得探测器在火星惯性坐标系的动力学方程.

当考虑处于静止大气模型时，将vg=0代入上述方程可得探测器在静止大气模型下的飞行动力学方程.

1.2 探测器受热及受载方程

总气动载荷N表达式［1］为

式中，v为探测器的速度标量;Q·为热流密度;C1=285.526［13］为常数;vc=3.547 km/s为火星的第一宇宙速度;Rd为探测器的曲率半径.

2 算例仿真及分析

2.1 仿真参数的确定

对两种大气模型下探测器动力学方程进行数值仿真，并进行仿真结果对比.火星探测器的初始位置选为远火点，其他初始参数如表1所示，探测器初始速度(单位:km/s)根据式(8)确定.

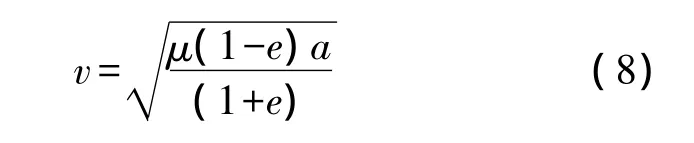
式中，e为轨道偏心率;a为半长轴.

表1 仿真初始参数值

2.2 仿真结果对比

算例1 选取轨道倾角i=4.297 2°，升交点赤经Ω=0.573°，其他的初始值见表1.图1、图2为两种大气模型下探测器轨道的半长轴a以及偏心率e变化对比示意图.

从图1、图2仿真结果可以看出，探测器多次穿越火星大气时，两种大气模型下轨道的半长轴a以及偏心率e变化值之间差距较小，但在旋转大气模型下探测器轨道的半长轴a以及偏心率e变化周期相较于静止大气模型下的变化周期变长，即出现了“滞后现象”.从而可知在设定一个目标轨道时，旋转大气模型对于任务耗时有一定的影响，所以在实际工程中应该考虑旋转大气对探测任务的影响.

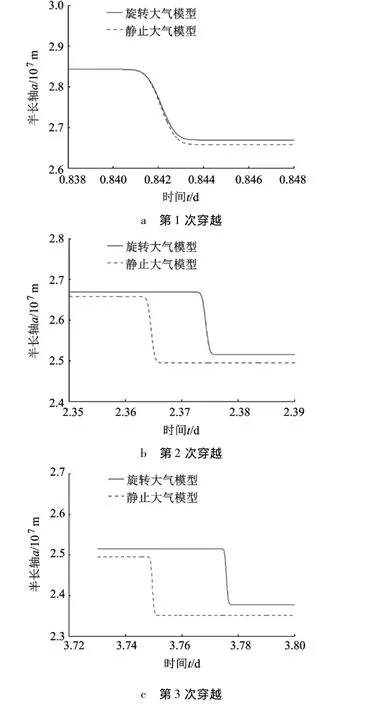
图1 不同时间段探测器半长轴变化曲线

图3、图4为两种大气模型下轨道倾角i以及升交点赤经Ω的变化示意图.仿真结果证明了高斯摄动理论［7］的正确性，即在静止大气模型下轨道倾角i以及升交点赤经Ω变化值为0;在旋转大气模型下，火星大气范围内轨道倾角和升交点赤经随时间连续减小，由于探测器受到大气影响的时间相较于整个运动时间而言很短，看似“突变”，且由于变化值很小，可以近似认为轨道平面不变.

在多次穿越大气时，两种大气模型下探测器所受的过载以及承热情况如图5、图6以及表2、表3所示.

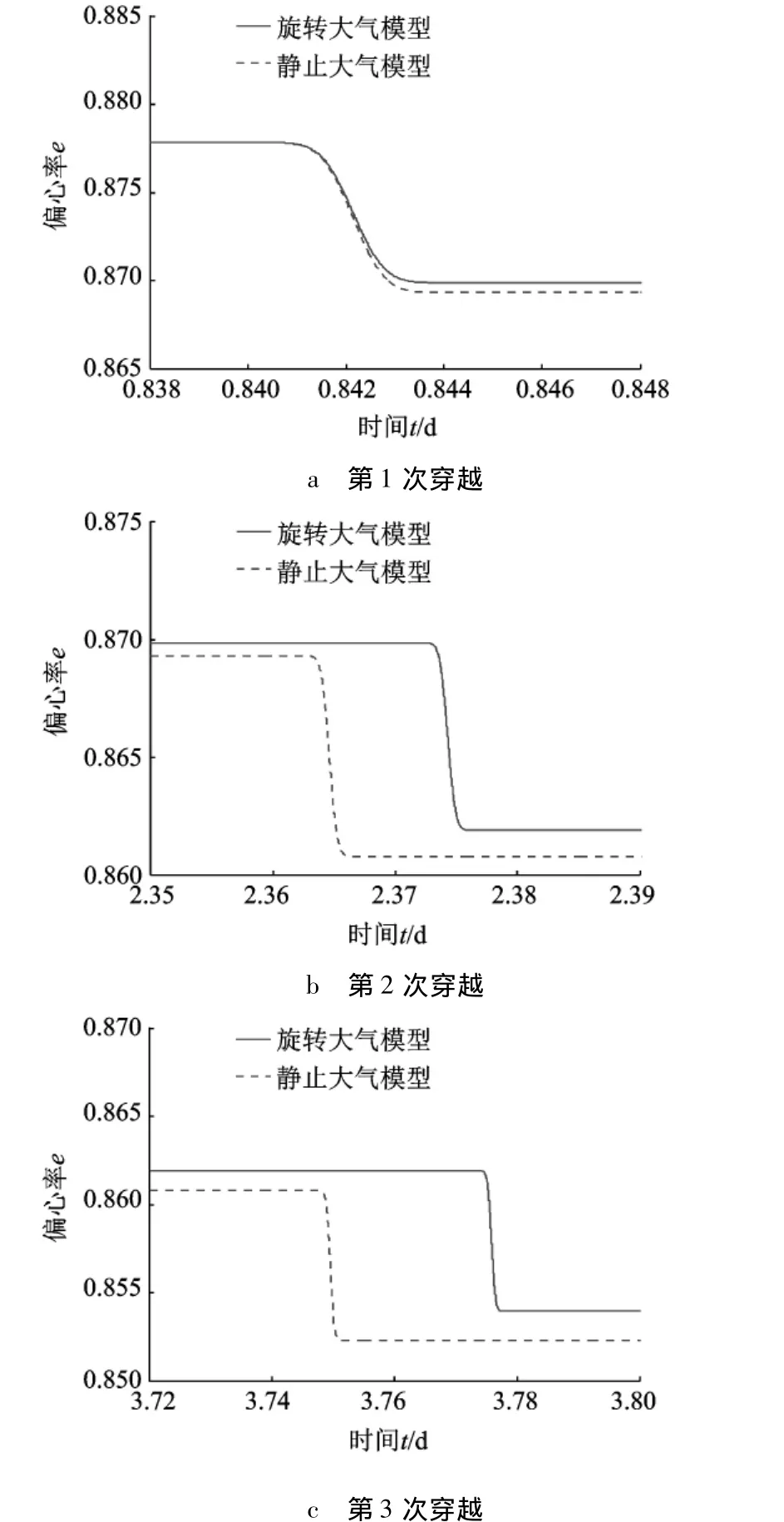
图2 不同时间段轨道偏心率变化曲线

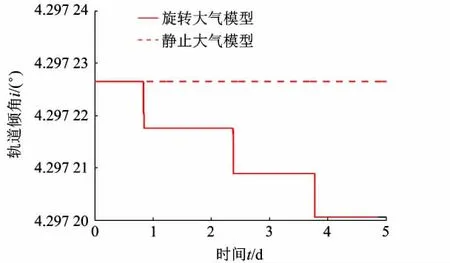
图3 探测器轨道与赤道面夹角变化曲线

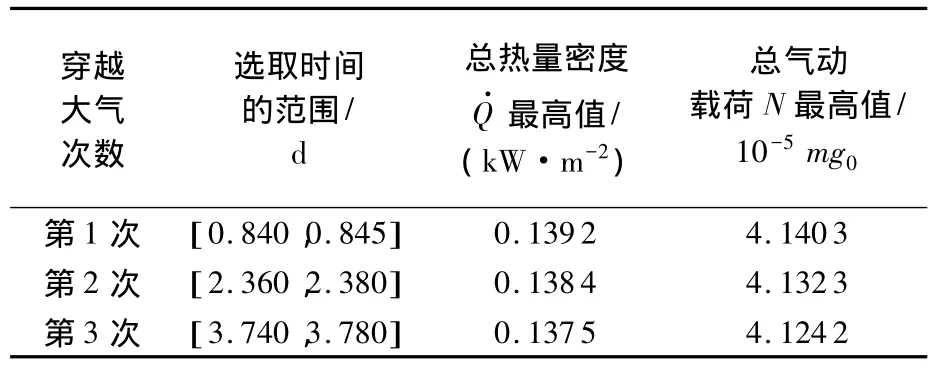
表2 静止大气环境下仿真结果

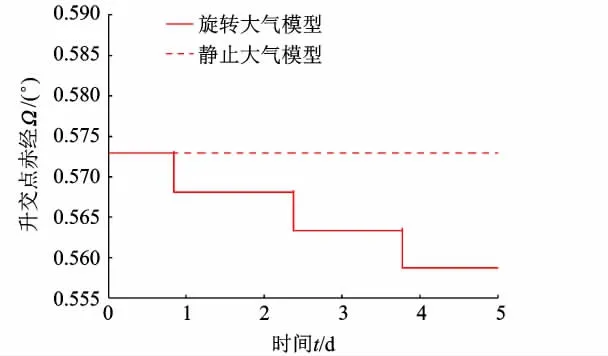
图4 探测器轨道升交点的赤经变化曲线

图5 不同时间段两种大气模型下受载情况

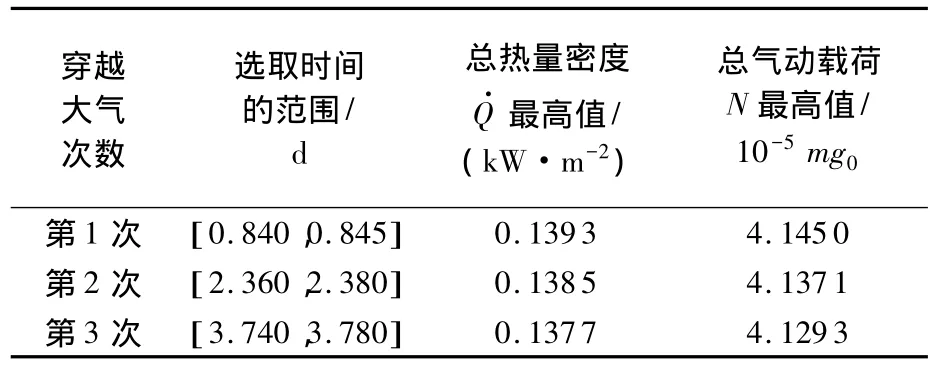
表3 旋转大气模型下仿真结果

图6 不同时间段两种大气模型下受热情况

由图5、图6及表2、表3的仿真结果可知，探测器在两种大气模型下承热和过载情况相差不大，相差最高值分别为0.000 2 kW/m2和1.924×10-5N.根据式(2)～式(4)以及式(6)～式(7)可知:探测器所受的大气阻力以及大气升力跟探测器与大气的相对速度以及大气密度有关.由于两种大气模型下大气密度的变化形式相同，而探测器和大气的相对速度绝对值不同，造成了热量密度以及气动载荷峰值的微小差异，由于两种大气模型下探测器轨道的半长轴和偏心率等(其他轨道参数根据相关公式得出)变化周期不同，从而穿越火星大气时间不同，探测器受载以及承热峰值出现的时间也不同.

本文选取不同的轨道赤经以及轨道倾角，对探测器轨道的参数变化形式进行了分析，通过研究可知当轨道倾角在0°～90°内变化时(升交点赤经值可由关系公式得出)，两种大气模型下部分轨道参数如半长轴、偏心率变化周期相差处于4%～10%范围内，其他轨道参数根据关系公式得出变化周期差距同样处于4% ～10%范围内.探测器的承热以及承载峰值相差处于0.065%～0.13%和0.054% ～0.06%范围内.

算例2 给定一个400 km×400 km的目标轨道，通过仿真结果得出相关结论.选取轨道的轨道倾角为10°，升交点赤经是60°，其他初始值见表1.在两种大气模型下探测器到达目标轨道随近火点高度的变化如图7所示.

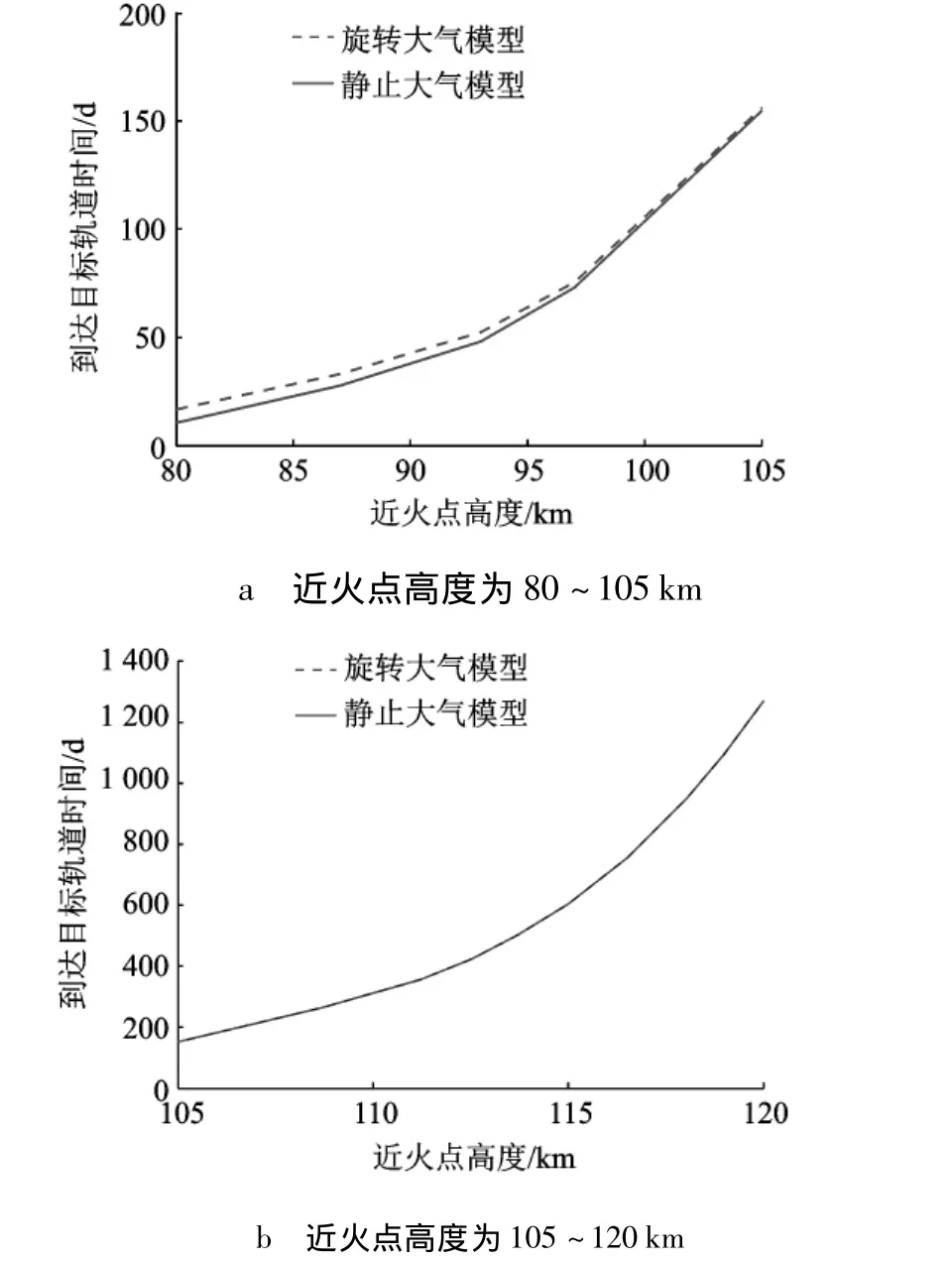
图7 探测器到达目标轨道随近火点高度的变化曲线

从仿真结果可以看出，在近火点高度低于105 km时，静止大气模型比旋转大气模型探测器任务耗时短，时间相差最大可达6.12 d.而在近火点高度大于105 km时，两种大气模型下探测器任务耗时基本相同.由于大气阻力以及大气升力跟探测器和大气的相对速度以及大气密度有关.所以当选取的近火点高度值较小时，大气密度值较大，虽然此时两种大气模型下探测器和大气的相对速度有差距，但差距很小，旋转大气对探测器的轨道变化造成的影响较为明显，所以当近火点高度较低时，两种大气模型下任务耗时差距较大，而当近火点较高时，大气密度值较小，虽然在旋转大气模型下探测器和大气的相对速度值会增大，但由于大气旋转角速度小，所以两种大气模型下任务耗时差距比较小.

两种大气模型不同近火点高度下，到达目标轨道探测器变轨过程中施加脉冲量如表4所示.

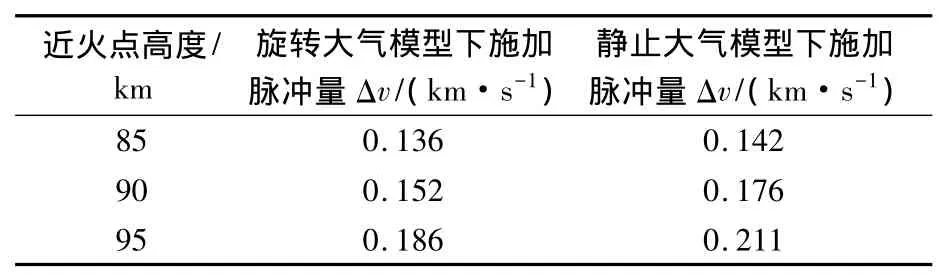
表4 两种大气模型下不同近火点高速探测器施加脉冲量

从表4可以看出，随着近火点的高度增大，探测器在两种大气模型下的速度改变量呈递增的趋势.由于两种大气模型下探测器受到的大气阻力以及大气升力不同，使得在两种大气模型下探测器的速度改变量不同，两者之间最大相差10.8%.

3 结论

本文建立两种大气模型下探测器的动力学方程，经过对比分析可知:

1)目标轨道近火点较低时，所处的大气密度值较大，两种大气模型下半长轴、偏心率等(其他轨道参数根据关系公式得出)的变化差距较明显，从而探测器轨道捕获任务耗时差距较大，而近火点较高时，大气密度值较小，两种大气模型下半长轴的变化差距很小，从而探测器轨道捕获任务耗时相差较小;

2)当选取相同近火点高度值时，旋转大气模型下轨道的轨道倾角以及升交点赤经有微小变化，而静止大气模型下轨道的轨道倾角以及升交点赤经保持不变;

3)探测器受载以及承热峰值相差不大，由于两种大气模型下，探测器穿越火星大气时间也不同，从而探测器受载及承热峰值出现的时间也不同.

References)

［1］闵学龙，潘腾，郭海林.火星探测器使命轨道捕获策略研究［J］.航天器工程，2008，17(6):39-43 Min Xuelong，Pan Teng，Guo Hailin.Analysis of orbit capture method for Mars vehicle ［J］.Spacecraft Engineering，2008，17(6):39-43(in Chinese)

［2］ David M C，James O A.Technologies of aerobraking［R］.NASA TM-02854，2011

［3］ Brice N.IAA Mars cosmic study report［R］.IAA-102-5528，1992

［4］ Nock K T，Friedlander A L.Elements of Mars transportation system［J］.Acta Astronautica，1987，15(6/7):505-522

［5］ Larson W J，Lindar K P.Human space flight:mission analysis and design［M］.New York:McGraw-Hill，1999

［6］ Angelo C，Emilio R A.Simplifified model for the evalution of the deltaV of ascent trajectories［C］//41stAIAA/ASME/SAE/ASEE JointPropulsion Conference and Exhibit.Tucson:Arizona，2005:267-298

［7］肖峰.人造地球卫星轨道摄动理论［M］.长沙:国防科技大学出版社，1995:178-192 Xiao Feng.Man-made earth satellite orbit perturbation theory［M］.Changsha:Press of National University of Defense Technology，1995:178-192(in Chinese)

［8］符俊，蔡洪，张士峰.气动力辅助双脉冲最优异面变轨问题研究［J］.导弹学报，2011，23(2):22-27 Fu Jum，Cai Hong，Zhang Shifeng.Research on optimal two-impulse aeroassisted orbital transfer［J］.Joural of Ballistic，2011，23(2):22-27(in Chinese)

［9］张文普，张成义，韩波.气动力辅助变轨的数值模拟［J］.力学季刊，2011，31(1):8-13 Zhang Wenpu，Zhang Chengyi，Han Bo.Numerical simulation of aeroassister orbit transfer［J］.Chinese Quarterly of Mechanics，2011，31(1):8-13(in Chinese)

［10］ Khalil K I.The drag exerted by an oblate rotating atmosphere on an artificalsatellite［J］.Applied Mathematics and Mechanics，2002，23(9):903-915

［11］ Christian J A，Grant W，Jarret L，et al.Extention of traditional entry，descent and landing technologies for human Mars exploration［ J］.Journal of Spacecraft and Rockets，2008，45(1):130-141

［12］ Braun R D，Manning R M.Mars exploration entry，descent and landing challenges ［J］.Journal of Spacecraft and Rockets，2007，44(2):310-323

［13］ Vaughan D，Miller H C，Brand G.A comparative study of aerocapture missions with a mars destination［C］//41stAIAA/ASME/SAE/ASEE Joint Propulsion Conference＆Exhibit.Tucson:Arizona，2009:225-263