一类具有非对称特性的隔振装置结构参数实验辨识方法

张呈波，张晓旭，宋汉文

(1．同济大学航空航天与力学学院，上海 200092;2．复旦大学力学与工程科学系，上海 200433)

一类具有非对称特性的隔振装置结构参数实验辨识方法

张呈波1，张晓旭2，宋汉文1

(1．同济大学航空航天与力学学院，上海 200092;2．复旦大学力学与工程科学系，上海 200433)

由于重力或装配应力等偏置力的影响，隔振元件的工作状态将会偏离原始平衡位置，进而产生具有非对称特性的动力学行为，其具体表现为系统的动态响应存在刚性漂移现象，且该刚性漂移的大小与外激励频率、幅值均存在复杂的关系;其次，由于振动传感器主要针对动态信号，对于零频附近的低频信号存在灵敏度低、测量误差大的缺陷。因而，对于系统响应中存在的刚性漂移信号，实验中往往无法准确测定，甚至可能丢失，这将给系统的动力学参数标定带来非常大的影响。本文针对该问题，建立了此类隔振实验装置的非对称动力学模型，并利用较为成熟的谐波平衡原理构造了一种简单的迭代算法，使其在刚性漂移信息缺失的情况下，仍然能够有效地辨识得到系统结构参数。通过数值仿真，验证了该算法的有效性，并将其应用于一款具体的隔振元件动力学参数辨识工作中。其结果表明，由该算法辨识得到的结构参数与系统真实动力学特性具有较高的吻合度，对于其它具有类似特性的隔振元件的设计及应用具有一定的参考价值。

非线性系统;参数辨识;谐波平衡;非对称;刚性漂移

Abstract:When the vibration isolator stays in a biased situation induced by gravity，assembly stress etc．，there will be a complex dynamic phenomenon with unsymmetrical characteristic such as rigid drift of the systems's dynamic response．Besides，this kind of drift has intimate relationship with external exciting frequency and its amplitude．On the other hand，the vibration sensors mainly suit for the measurement of dynamic signals．Therefore，there will be some deficiencies like blunt sensitivity and low accuracy in the measurement of nearly constant and slowly varying signals．When these sensors are applied to the experiment of the unsymmetrical systems mentioned above，the rigid drift data will be measured inaccurately or even lost，which can cause great difficulty to the system's parameter identification．According to this problem，a simple iteration algorithm based on the principle of harmonic balance was constructed for the parameter identification of unsymmetrical dynamic systems so that the identification is still efficient in the case of the losing the rigid drift information．As a numerical simulation example，the algorithm has been successfully applied to the parameter identification of a real vibration isolator．The results show that the identified parameters have satisfying coincidence with the experimental ones．

Key words:nonlinear system;parameter identification;harmonic balance;unsymmetrical system;drift

非线性动力系统具有丰富的动力学行为。辨识非线性系统参数是研究其动力学现象的重要基础。基于优化策略的模糊算法被广泛应用于非线性系统的参数辨识工作中，如:遗传算法［1－2］、神经网络算法［3－6］等。这些算法仅需构造简单的搜索模式，经过有限次的迭代运算，辨识出系统中未知的参数。不过，这些方法也存在着抗噪能力一般、初值依赖性强的缺点。

基于谐波平衡原理的辨识方法也是参数辨识的有效方法，这种方法虽然理论推导复杂，但却能够直接得出用于参数辨识的线性代数方程，并且具有精度高、抗噪能力强的特点。在理论上，该方法发展出了稳态响应的参数辨识算法［7－9］、极限环响应的参数辨识算法［10］及混沌响应的参数辨识算法［11－12］。在实验中，如金属橡胶［13］等非线性元件的参数辨识也是根据谐波平衡原理推导的。该方法的应用已比较成熟可靠。

本文以谐波平衡原理作为参数辨识的理论基础，通过振动台基础激励正弦扫描实验，将其应用到某卫星上精密仪器的隔振实验模型的结构参数辨识中。

首先，由于被隔振物体重力、装配应力等偏置力的影响，隔振元件平衡位置的偏移是不可避免的，这就造成了实验系统的非对称性，改变隔振元件动态下的刚度或阻尼。针对此事实，建立了非线性隔振实验装置的非对称动力学模型。

其次，对于非线性系统，由于系统的非对称性引起系统的静平衡位置与动态平衡位置不再重叠，具体表现为系统位移响应出现刚性漂移，即其位移响应频谱在零频处具有随激励幅值和激励频率变化的非零幅值。而在实验中，由于常用的位移传感器不便于确定参考零点，测量范围有限且精度偏低，既无法准确测得位移响应中存在的刚性漂移信息，也不能获得高精度的系统响应数据。而加速度传感器能测得高品质的系统响应信号，但无法恢复位移响应中的刚性漂移信息。因此，本文在用加速度传感器测得满意的响应数据的前提下，运用谐波平衡原理构造一种简单的迭代算法，使其在刚性漂移信息缺失的情况下，仍然能够有效地辨识得到系统结构参数。通过数值仿真来验证该算法的有效性，并将其应用于隔振实验装置的结构参数辨识。

1 理论基础

1.1 非线性隔振器动力学建模

现有隔振器的建模大多是以幂级数多项式的形式逼近［13－16］，都能得到较好的辨识效果。本文在不考虑迟滞效应的前提下，以多项式非线性阻尼和多项式非线性刚度来逼近非线性隔振实验系统。

如图1所示，非线性隔振系统可假设为一个单自由度的具有非线性刚度及非线性阻尼支承特性的动力学系统。其简化模型如图2所示。

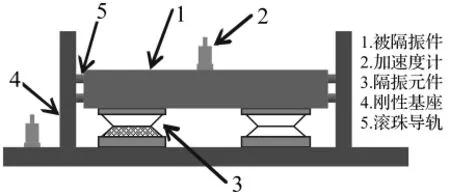
图1 非线性隔振器示意图Fig．1 Sketch of nonlinear isolator

图2 非线性隔振器动力学模型Fig．2 The dynamic modal of nonlinear isolator

设质量块位移为x(t)，地基激励为q(t)，且该系统的阻尼及刚度特性均为立方非线性模式，建立该系统动力学方程为:

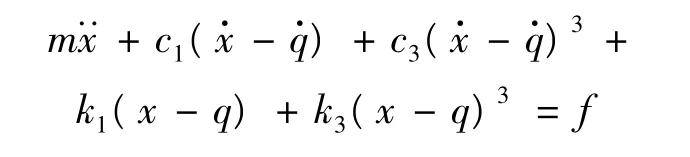
式中，f为偏置力。令~x=x－q，则上式可简化为:

考虑该系统受到重力及装配应力的影响，则偏置力表现为一个常力，记为f=Fconst。此时，系统的静平衡位置将发生偏移，新平衡位置X满足方程:

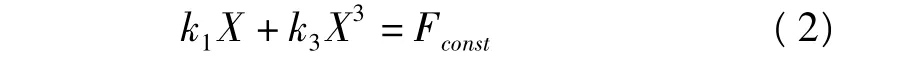
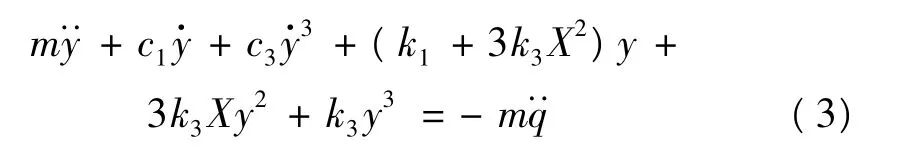
从上式可以看出，偏置力引起了刚度项的变化。

进一步，考虑材料本构中可能存在的非对称特性，

式(3)可进一步修正为:

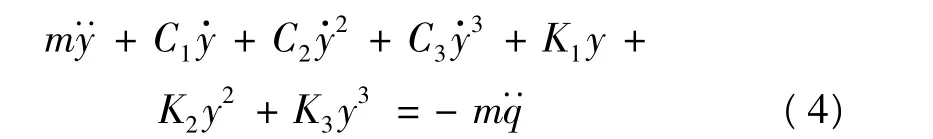
至此，我们建立了具有非对称形式的非线性隔振器的动力学模型。

1.2 辨识算法构造

根据谐波平衡原理，若采用单频简谐激励，即:

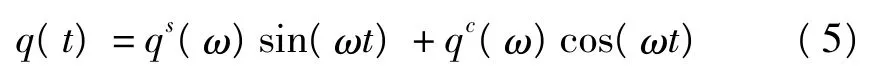
其中qs(ω)、qe(ω)分别为对应于频率ω的正弦及余弦项系数，则系统(3)在渐进稳定的前提下具有周期形式的稳态响应，其傅里叶展开为:

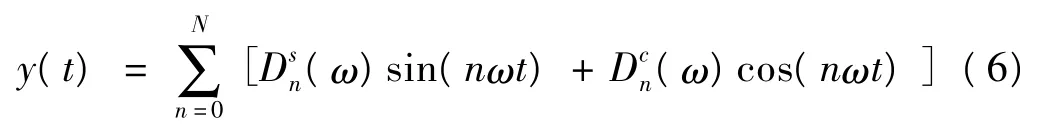
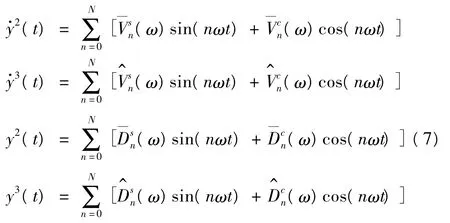
式中:

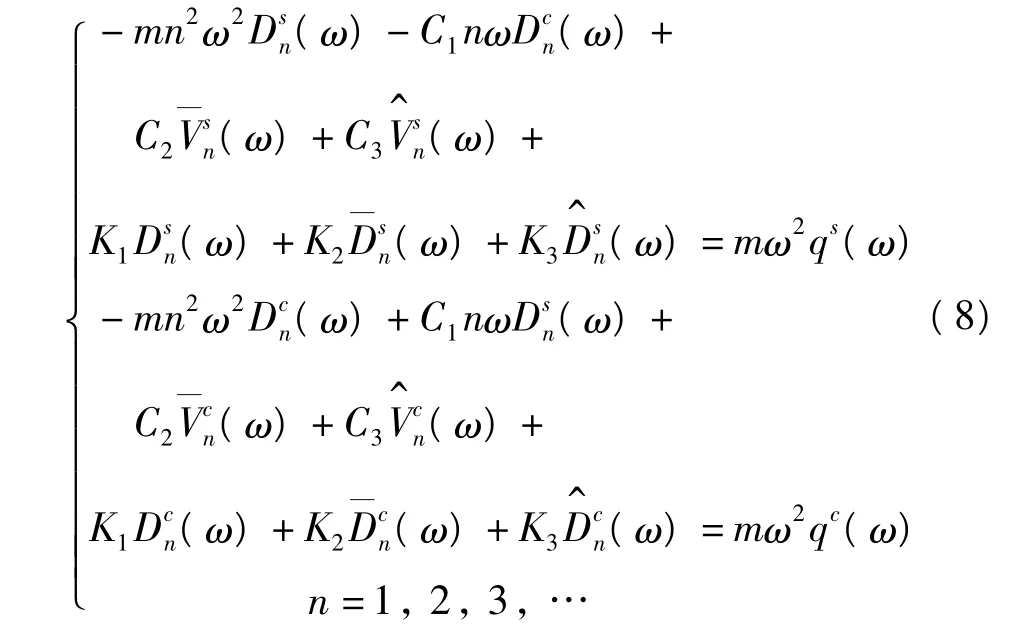
假设系统的质量m已知，待辨识参数为Ch、Kh，h=1，2，3共六个参数。考虑到系统响应中，主谐波占有较高的能量比例，且具有较高的信噪比，因此我们通过(8)式的主谐波形式建立未知参数的辨识方程。此时n=1，考虑不同的激励频率ωr，r=1，2，…，N，可构造出辨识方程:

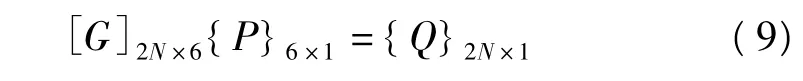
式中:

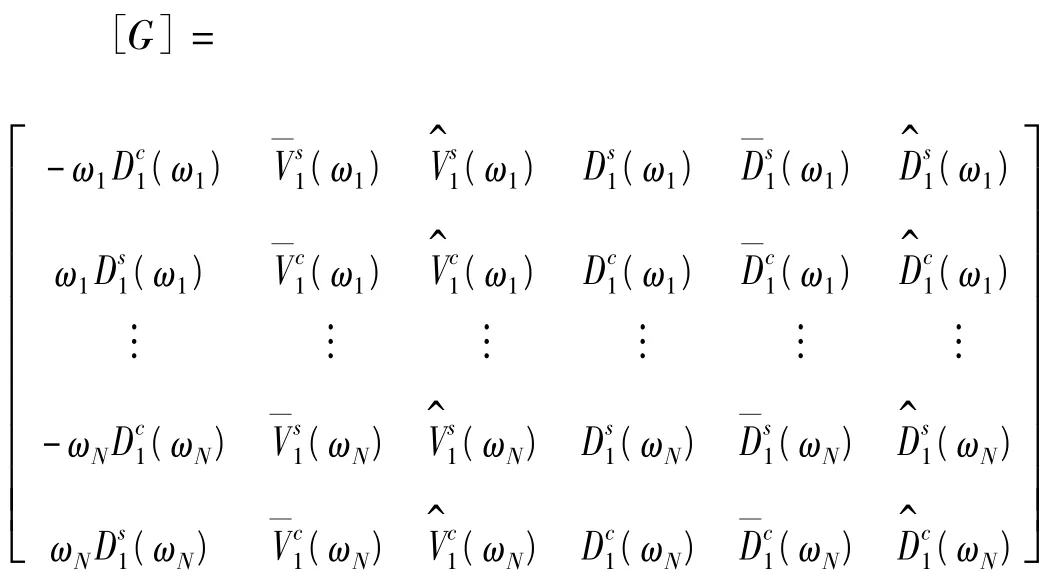
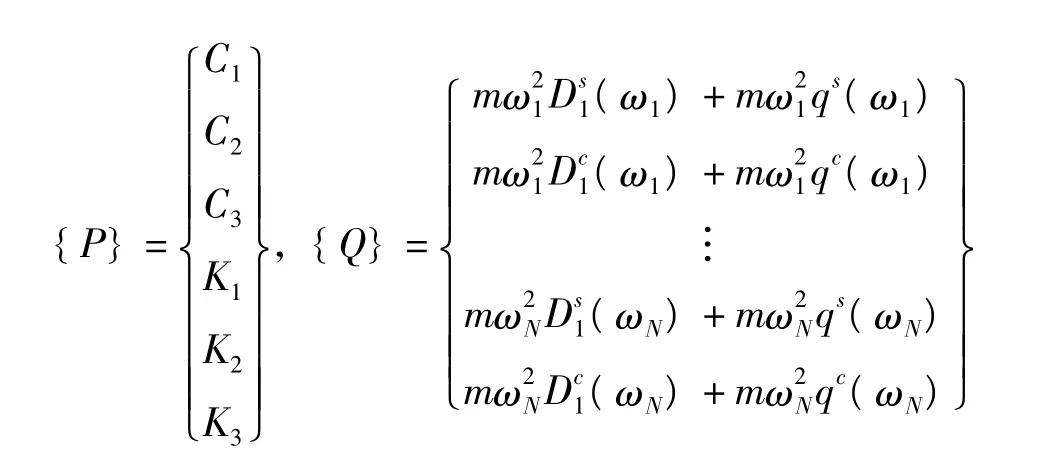
由(8)式可写出未知参数的辨识结果为:

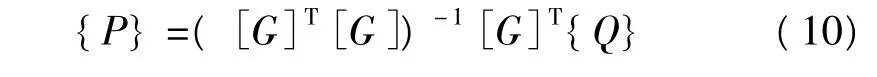
2 数值算例

2.1 误差分析

通过前文的理论分析，我们构造出了如式(10)所示的非线性参数的辨识算法。然而在真实实验中，由于传感器对定常及较低频信号的测量存在较大误差，甚至缺失，因此必须对该算法的有效性进行分析。记由实验所测或还原得到的位移信号为(t)，对照式(6)，满足:

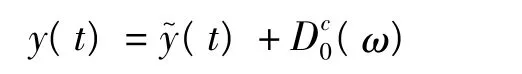
因此，系数矩阵［G］中，位移平方、立方项的主谐波系数将会被修改。记真实系数分别为，实验所得为，两者具有如下关系:而其余系数不变。显然，刚性漂移信息缺失时，辨识误差全部由系数矩阵［G］的第5、6列引起。

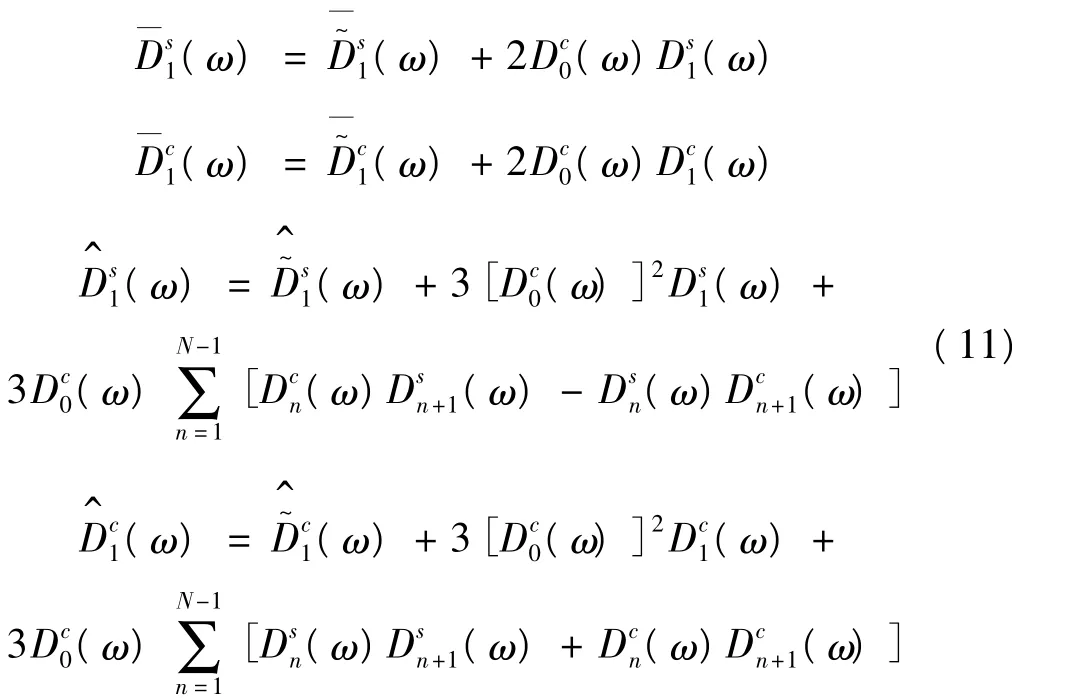
基于上述分析，本节主要考察非对称特性的强弱与动态平衡位置偏离程度之间的定量关系，以及刚性漂移信息的缺失对辨识精度的影响。

使用如式(4)所示的动力学模型，设置各参数为:m=2，C1=1．6，C2=－0．1，C3=－0．4，K1=8，K2=－0．6，K3=－4。采用定加速度步进激励方式，加速度幅值(Acc)分别为0．4、0．5、0．6和0．7。该设定下，系统位移响应及加速度响应的主谐波幅频曲线为:

考虑到位移响应中，主谐波响应占有主要成分，因此对于刚性漂移幅值的定量考察，我们也以主谐波响应幅值为参考。各激励幅值、频率下，刚性漂移幅值与主谐波响应的比例关系如下:

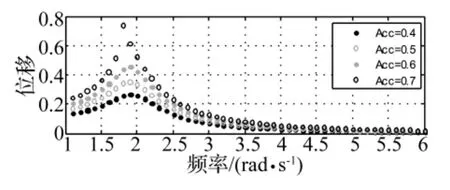
图3 位移响应的主谐波幅频曲线Fig．3 The main harmonic amplitude-frequency curve of displacement response

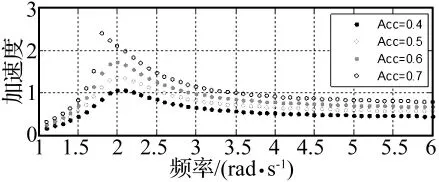
图4 加速度响应的主谐波幅频曲线Fig．4 The main harmonic amplitude-frequency curve of acceleration response

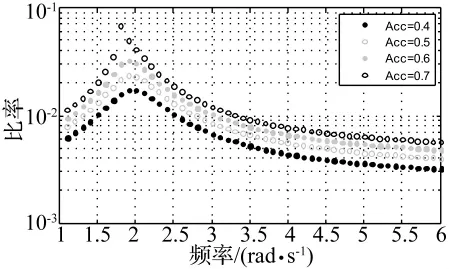
图5 动平衡幅值相对主谐波响应的比率曲线Fig．5 The ratio of dynamic balance’s amplitude to main harmonic response

从图5可以看出，激励幅值越强、激励频率越接近系统固有频率，则响应中的非对称效应越明显，刚性漂移偏离越厉害。因此可以推测，在刚性漂移信息缺失的情形下，为使非线性参数的辨识结果具有更高精度，实验中应选取远离固有频率、小幅值激励条件下的响应数据。

依照上述经验，我们定量考察动平衡信息缺失对辨识精度的影响。选取激励幅值为0．4、激励频率为2．5～3．5 rad/s，此时刚性漂移幅值与主频响应幅值的比例为0．01～0．005。各非线性参数的辨识结果如表1所示:

表1 非线性参数辨识结果Tab．1 The results of nonlinear parameters identification

由上表可以看出，尽管非对称强度极弱，但刚性漂移信息缺失时，动力学系统中平方项系数的辨识结果却有十分显著的误差。因此，我们必须对辨识算法(9)进行适当的改进。

2.2 算法改进

首先，从表1可以看出，尽管平方项系数的辨识误差很大，但系数正负性质的判断是正确的。其次，由图5可见，在远离共振频率时，刚性漂移幅值与主谐波幅值的比率不明显依赖于频率及激励幅值。因此，我们可以结合首次辨识的结果和主谐波幅值，构造迭代算法，使得动力学系统中平方项系数的辨识结果收敛至足够的精度。具体迭代过程如下:

步骤1:记主谐波幅值为

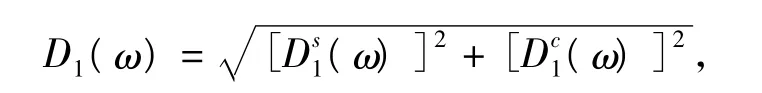
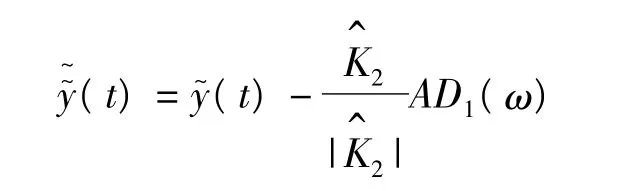
式中:A为修正倍率。将其作为真实位移的近似恢复，用于第一次迭代参数辨识。

步骤2:将前一次辨识得到的结构参数代入(4)式进行数值计算，求得相应激励频率下的刚性漂移信息0(ω)，令，作为真实位移的近似恢复，用于进一步的迭代参数辨识。

步骤3:重复步骤2，直至辨识结果收敛到足够的精度。

按照上述迭代步骤，令修正倍率A为0．01，对表1所得结果进行迭代计算。迭代辨识结果如下:

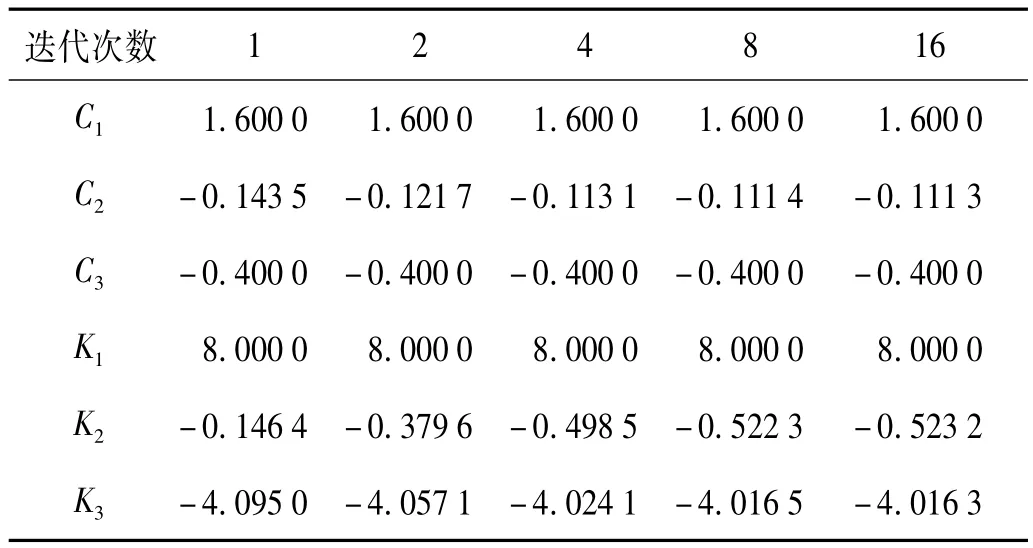
表2 迭代辨识结果Tab．2 Identified results

由上表可以看出，该迭代算法具有较快的收敛速度，其不足之处在于平方项系数C2，K2辨识结果的相容性稍有欠缺，即不能完全收敛至预设值。对比表1还可看出，迭代算法可使辨识精度大幅提高，其辨识最大相对误差已从534．45%降至12．8%，基本满足实验辨识的要求。

3 实验分析

通过数值分析，本文已经验证了基于谐波平衡原理的非线性参数辨识算法的可靠性。因此，我们将该辨识算法应用于非线性隔振装置非线性参数的实验辨识，其实验装置如图。

图6 隔振器实验装置Fig．6 Experimental device of isolator

该隔振系统被隔振件的质量为m=1．86 kg。实验装置通过基座固定在垂直振动台上，采取步进恒加速度正弦激励的方式，加速度幅值为0．4 g，采样频率1 024 Hz，稳态响应采样时长80 s，采集基座及被隔振件的稳态加速度响应。

通过傅里叶变换可得该系统加速度响应的主谐波幅频曲线，如下图。

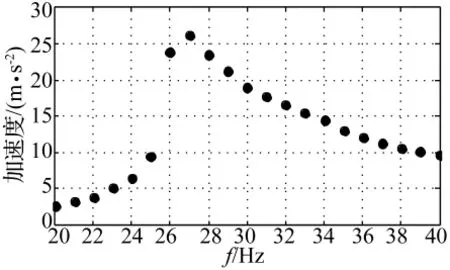
图7 实测加速度响应幅频曲线Fig．7 Experimental amplitude-frequency curve of acceleration response

按照数值算例的经验，经过40次迭代运算，得到各参数辨识结果为:

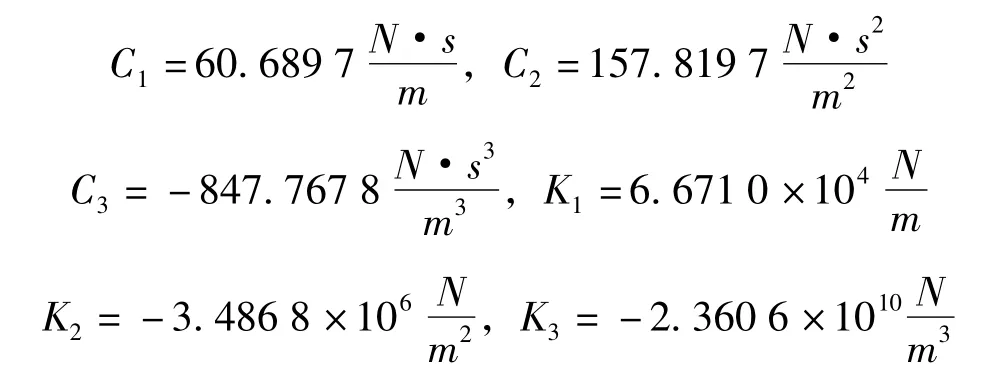
为更形象地对比辨识结果，将上表所得参数代入方程(4)进行数值仿真，所得位移响应主谐波频响与实测位移频响的对比图如下。

根据辨识得到的结构参数，可得隔振器的载荷－位移曲线。

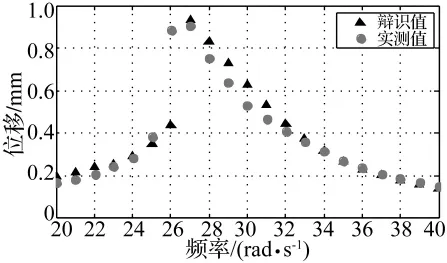
图8 位移幅频曲线对比Fig．8 Comparison of displacement’s amplitude-frequency curve

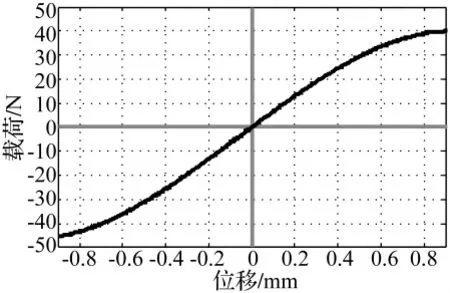
图9 隔振器载荷－位移曲线Fig．9 Force-displacement curve of the isolator

至此，本文基本完成了非线性隔振装置各结构参数的辨识工作。通过图8可以验证，本文辨识所得的各结构参数具有较高的精度。从图9可以看出该实验装置具有的非对称特性。

4 结论

本文针对一类特定的非线性隔振实验装置，考虑偏置力(如重力等)对实验系统的作用，建立了其非对称动力学模型，使得模型更加准确的描述了系统真实的动态特性。

利用谐波平衡原理，构造了系统动力学参数的迭代辨识算法，并通过数值仿真，验证了辨识方法的有效性。解决了由于位移响应的刚性漂移信息的不准确或缺失对辨识精度的不良影响。

通过辨识所得到的结果与实验结果的对比，可以看出，此辨识算法对于具有非对称性特性的非线性实验系统的参数辨识，有较高的辨识精度，也证明了本文针对非对称性所建立的模型的合理性。并为此类隔振实验装置的结构参数辨识提供参考。

［1］Giorgio M，Giuseppe Q，Carlo M G．Genetic-algorithm-based strategies for dynamic identification of nonlinear systems with noise-corrupted response［J］．Journal of Computing in Civil Engineering，2010，24(2):173－187．

［2］Madar J，Abonyi J，Szeifert F．Genetic programming for the identification of nonlinear input-output models［J］．Industrial＆Engineering Chemistry Research， 2005， 44 ( 9 ) :3178－3186．

［3］Bidyadhar S，Debashisha J．Nonlinear system identification using memetic differential evolution trained neural networks［J］．Neurocomputing，2011，74(10):1696－1709．

［4］Xie W F，Zhu Y Q，Zhao Z Y，et al．Nonlinear system identification using optimized dynamic neural network［J］．Neurocomputing，2009，72(13):3277－3287．

［5］Sharan Anand M．Identification of parameters of nonlinear duffing oscillators subject to sub and super harmonic excitation using artificial neural network ( ANN ) technique ［J］Advances in Vibration Engineering，2008，7(3):253－260．

［6］Patra J C，Pal R N，Chatterji B N，et al．Identification of nonlinear dynamic systems using functional link artificial neural networks［J］．IEEE Transactions On Systems Man And Cybernetics Part B-Cybernetics， 1999， 29 ( 2 ) :254－262．

［7］Ye M，Dou S G，Zhang W，et al． Nonlinear identification of systems with parametric excitation ［J］． Science China Technological Sciences，2011，54(8):2080－2089．

［8］Narayanan M D，Narayanan S．Padmanabhan C．Parametric identification of nonlinear systems using multiple trials［J］．Nonlinear Dynamics，2007，48(4):341－360．

［9］Thothadri M，Casas R A，Moon F C，et al．Nonlinear system identification of multi-degree-of-freedom systems ［J ］．Nonlinear Dynamics，2003，32(3):307－322．

［10］Thothadri M，Moon F C．Nonlinear system identification of systems with periodic limit-cycle response［J］．Nonlinear Dynamics，2005，39(1):63－77．

［11］Liang Y，Feeny B F．Parametric identification of a chaotic base-excited double pendulum experiment［J］．Nonlinear Dynamics，2008，52(1):181－197．

［12］Yuan C M，Feeny B F．Parametric identification of chaotic systems［J］．Journal of Vibration and Control，1998，4(4):405－426．

［13］Hao H R，Bai H B，Hou J F，et al．Generalized resuming force model for metal-rubber［J］．Journal of Vibration and Shock，2008，11(27):106－109．

［14］Shi L，He L． Study on parameter identification for magnetorheological dampers［J］． Journal of Vibration and Control，2009，28(1):131－133．

［15］Lu C，Bai H，Xin W T．Parameter identification of dynamic model of hysteretic vibration isolation system with unsymmetrical elasticity and viscous damping［J］．Journal of Vibration and Shock，2007，26(6):110－112．

［16］Wu R A，Feng J Q，Wang Y J，et al．Nonlinear parameter identification and character research of rubbervibration isolating system［J］．Chinese Quarterly of Mechanics，2007，28(2):281－285．

Experimental identification method for the nonlinear vibration isolator with unsymmetrical dynamic characteristics

ZHANG Cheng-bo1，ZHANG Xiao-xu2，SONG Han-wen1
(1．School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China;2．Department of Mechanics and Engineering Science，Fudan University，Shanghai 200433，China)

O322;TB123

A

国家自然科学基金(11032009)

2011－11－10修改稿收到日期:2012－01－05

张呈波男，硕士，1987年生

宋汉文男，博士，教授，1962年11月生