基于统计线性化的非线性随机振动虚拟激励法研究及应用

罗晓峰，项贻强

(1.浙江大学 土木工程系，杭州 310058;2.浙江工业职业技术学院，绍兴 312000)

我国是一个多发地震国家，确保桥梁结构在地震荷载下的安全运营具有十分重要的意义，以往的经验表明进行科学合理的抗震设计是减轻因地震造成损失的有效途径，目前国内外桥梁结构的抗震设计中，反应谱法、时程法以及随机振动法等传统的计算方法已经得到广泛应用［1-3］。由于地震地面运动实际上是一种随机激励，因此结构的抗震设计以结构的随机地震响应为基础更为科学、合理。随机振动法以功率谱密度作为分析的核心，所以又称功率谱法，这种方法可以较充分地考虑地震发生的统计概率特征，并且适合于跨度较大、结构较复杂的多点支撑的桥梁，被认为是一种较为先进合理的分析工具，1995年，欧洲结构抗震设计规范(Eurocode 8)把功率谱方法作为结构抗震设计计算的工具［4-5］，我国现行的公路桥梁抗震设计规范也将功率谱法作为结构抗震设计计算的方法之一。Penzien等在80年代初曾将核电站管线简化后，分别从时域和频域的角度研究了其在不均匀场地激励下的安全问题，得出忽略参振振型之间的相关性和场地不均匀性都会导致很大的误差;Lin等将输油管线视为有多个支点的连续梁，用随机振动法研究了其抗震性能;Perotti、Harichandran等也研究了多点随机振动方法。上述方法由于计算效率低，且只能处理较简单的结构，难以在实际的桥梁工程中得到广泛地应用。近年来，林家浩教授［1］从计算力学的角度提出了简单易行，计算效率较高，并在理论上属精确算法的虚拟激励法，张笈玮等［6］在传统虚拟激励法的基础上，提出了一种计算非平稳地震激励下结构峰值响应均值的简便算法;江洋等［7］提出了一种只需少量振型即可获得高精度的虚拟激励算法—修正的绝对位移法。但是到目前为止，虚拟激励法只是成功地解决了结构线性随机地震响应计算的工作量问题，对于计入非线性的桥梁结构的抗震分析，国内外还还没有较深入研究，因此探讨与发展非线性体系随机地震响应的虚拟激励法显得十分迫切与重要［8］。

本文在统计等效线性化的基础上，应用FAP数值解法［9-11］，提出了一种简便、高效、实用的，可以考虑结构非线性的改进的虚拟激励法，这种方法避开了分解位移和求解拟静模态矩阵的复杂过程，可以在一般的通用有限元软件中应用。作为算例，以跨径75m+55m的单塔双索面预应力混凝土斜拉桥为背景进行抗震分析，应用不同的抗震分析方法计算其位移、速度、加速度响应功率谱密度，及其位移响应历程和轴力响应值，说明基于统计线性化的绝对位移直接求解的虚拟激励法的精确性。

1 统计线性化方法

1954年美国学者Booten［12］提出了一种可以处理非线性力学系统随机响应问题的方法—统计等效线性化方法，对于n个自由度的非线性力学系统可以用如下微分方程式表达，即:

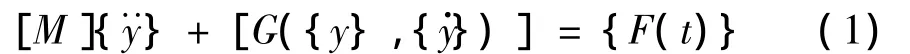
式中［M］是一个n阶的结构质量矩阵;［G({y}，{})］为非线性恢复力和阻尼力之和的等效矩阵。

建立与非线性系统等效的线性化方程:

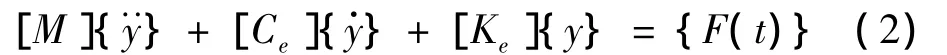
式中［Ce］为等效粘阻系数矩阵，［Ke］等效刚度矩阵。

将式(1)与式(2)作差，于是得到:

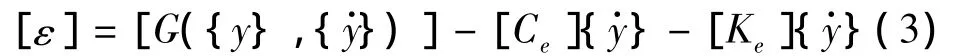
式中{y}={y(cij，kij，t)}，为方程(2)的稳态解，其中cij，kij为系数矩阵［Ce］，［Ke］的元素。

误差矩阵［ε］是cij，kij的函数，统计线性化的实质就是要求合理地选择cij，kij，使

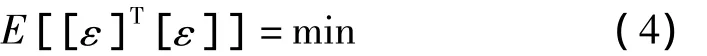
式中E是数学期望。

通过数学计算，可以求得式(4)的解，进而求得非线性系统的等效线性刚度［Ke］和等效粘滞阻尼［Ce］。

2 绝对位移直接求解的虚拟激励法

由文献［1］中传统虚拟激励法的求解原理，可知在求解虚拟动态相对位移和虚拟静位移时，都需要计算并提取拟静模态矩阵A=-·，十分麻烦，而且有些软件没有矩阵提取功能，所以一般不能在通用有限元软件中求解，需编制相应的专用求解程序，要解决这一问题，可参考文献［7］。

为此，本文在文献［13］研究的基础上，提出了基于统计线性化的绝对位移直接求解的虚拟激励法，具体实施如下:

将方程(2)写成分块矩阵的形式［1，13］:

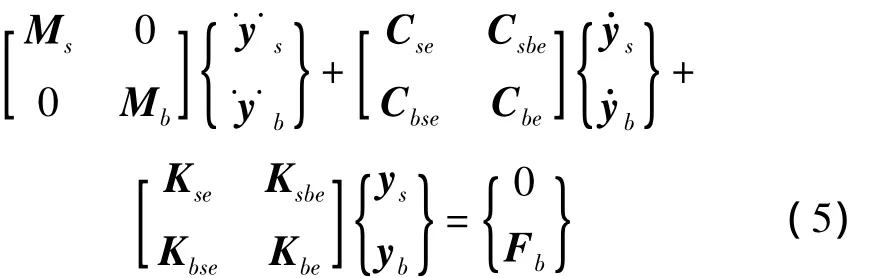
式中yb代表N个支座的地面强迫位移，ys代表非支座节点的位移，Fb代表地面作用于N个支座的力，下标s，b代表结构内部节点自由度和支座节点自由度。

构造虚拟加速度激励:

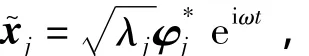
将与Mb的乘积作为Fb代入式(5)，可得:

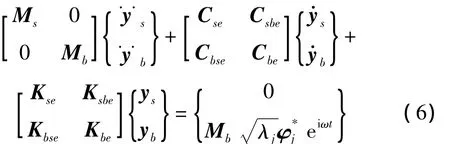
将上式按第二行展开，得:

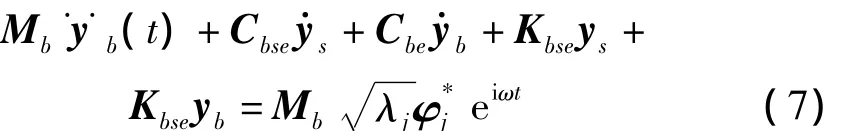
将上式两边同时乘以M-1b，得:

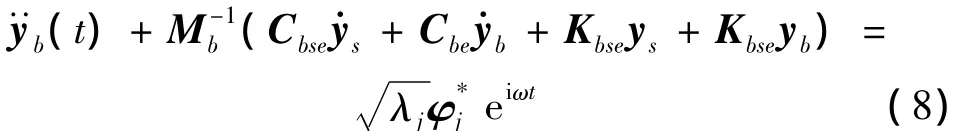
显然，当Mb为一大质量，即Mb→∞时为零，则由式(8)可得支座虚拟加速度激励为:

由上述可知，只需对支座赋予一大质量块，并对大质量块施加虚拟力激励，即可实现虚拟加速度激励的加载，则支座虚拟速度激励和虚拟位移激励为:

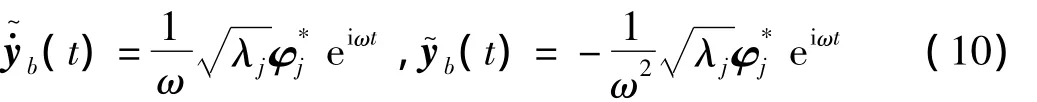
将式(6)按第一行展开，可得:

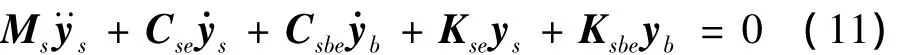
将式(10)代入式(11)，可以求得虚拟绝对位移˜ys，按照虚拟激励法，绝对位移的功率谱矩阵为:

关于传统的随机振动求解原理，以及动态相对位移自功率谱密度、拟静态相对位移自功率谱密度及两者之间的互功率谱密度的求解，很多学者对其进行了深入的研究，这里不再赘述。

3 算例分析及比较

3.1 工程背景及模型信息

取一典型的桥长130 m、跨径布置为75+55 m的两跨单塔双索面预应力混凝土斜拉桥为例，其塔墩梁为固结的结构体系。主梁截面为双实心边主梁大悬臂截面，主梁中心高1.9 m，顶板宽38 m，悬臂长4.5 m，主梁侧实心梁宽3 m，背跨侧实心梁宽4 m，实心梁间顶板厚0.28 m。背跨部分梁段由于配重的需要而增设底板形成箱型截面。主梁采用双向预应力体系，主塔为钢筋混凝土斜塔，塔中心线与水平夹角为75°，桥面以上垂直高为50.7 m，主塔采用变截面实心矩形，顺桥向截面高度从3 m(塔顶部)变化到8 m(桥上塔根部):横桥向宽度为2.5 m，用通用有限元软件ANSYS进行建模，主梁、主塔采用C50混凝土，斜拉索采用高强钢丝PSEM7-241，典型主梁截面型式用有限元模拟如图1所示，计算模型对塔用空间梁单元beam4进行离散，主梁用带刚臂的空间梁单元beam4简化为鱼骨刺形，斜拉索采用link10单元，左桥端给予竖向平移自由度约束，右桥端给予横向的平移自由度约束，索塔底部完全约束，索单元和梁单元采用铰约束，如图2所示。

图1 典型的主梁截面型式(单位:m)Fig.1 Typical girder section type(unit:m)

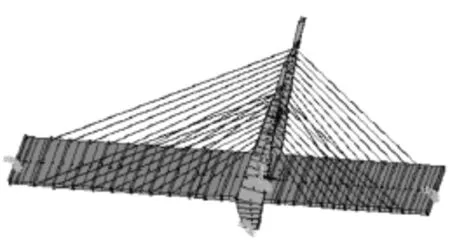
图2 斜拉桥模型Fig.2 Mode of cable-stayed bridge

3.2 计算概要

为了验证绝对位移直接求解的虚拟激励法的正确性，本文应用统计线性化方法将体系线性化，之后采用有限元软件中的随机振动模块和谐响应模块进行分析，线性化过程及问题的求解可参考文献［9］，文献中充分利用计算机的特点并结合FAP数值解法较好地解决了多自由度非线性系统在随机激励下的响应问题，FAP是统计线性化方法的数值解法，能方便的用各种算法语言编制出相应的计算机程序代码，本文应用FORTRAN 90编制了FAP算法的程序，以实现结构的线性化，限于篇幅，不再赘述。

对于本文提出的绝对位移直接求解的虚拟激励法，可以用简谐响应分析中的Full法，隔振支座采用combin40，刚度为k=6×106N/m，模态分析时取前150阶振型，振型参与质量达到97%，以保证算法的足够精度，在采用绝对绝对位移直接求解的虚拟激励法时，在模型基底的4个支坐节点上附加mass21大质量单元，大质量单元与支座节点刚接，质量取主桥质量的106倍，然后释放x，y方向自由度的约束，按上述理论提出的方法，对每个大质量块施加虚拟力然后进行谐响应分析，求得计入非线性后的虚拟激励响应，进而按照式(12)求得绝对位移的功率谱密度矩阵。计算时输入的功率谱采用由文献［7］提出的GB50011-2001修正反应谱模型迭代得到的实用地震动功率谱［7，14-15］。一致地震动参数:7度设防，Ⅲ类场地，第一组设计地震分组，视波速取100m/s，相干函数采用L-W模型，整个结构采用Rayleigh阻尼，取基底四个节点进行三向一致激励(基地的四个节点分别为:左桥端约束节点、右桥端约束节点以及索塔底部横桥向中心线两侧的约束节点)。

3.3 绝对位移法与随机振动法的结果对比分析

图3和图4分别给出了该斜拉桥主跨和背跨跨中的响应功率谱密度图，包括位移、速度和加速度的响应功率谱密度。

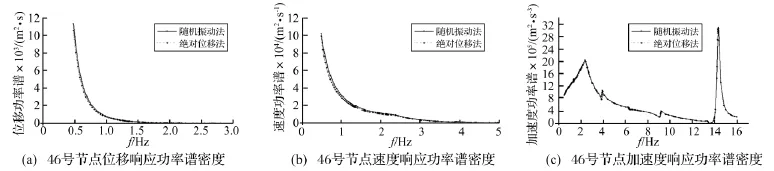
图3 主跨跨中响应功率谱密度对比图Fig.3 Contrast of response power spectral density in the middle of main span

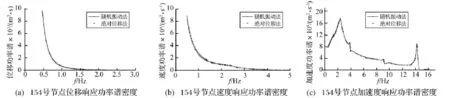
图4 背跨跨中响应功率谱密度对比图Fig.4 Contrast of response power spectral density in the middle of back span

从计算结果可以看出，将体系线性化之后，两种算法的计算结果基本一致，并且通过研究发现，其它主梁和主塔节点的响应功率谱密度也有类似规律，说明绝对位移法的正确性。再者，通过观察对比，发现绝对位移法计算得到位移、速度和加速度响应功率谱密度值较之于随机振动法计算得到的值均偏小，从曲线与横坐标围成的面积来分析，绝对位移法得到的地震随机振动波的均方值偏小，即施加给斜拉桥的能量偏小，说明随机振动法是一种偏于保守的抗震分析方法。

由于输入的加速度功率谱密度的频率范围为0.48-15.9 Hz，因此图中没有体现频率在0-0.48 Hz之间的曲线段，实质上，在频率为零的附近，输入的激励会导致结构的响应功率谱密度急剧增大，一般的功率谱密度模型会对地震动低频分量进行合理缩减，在f=0时，功率谱密度一般为零［2］。对于位移和速度响应功率谱，在f≥3 Hz之后，其值很小，因此在图中没有体现，对于加速度反应谱，在f≥3 Hz后，其值有一定范围的波动，变化曲线如图3、图4的(c)图所示。

绝对位移直接求解的虚拟激励法与传统的随机振动法相比，其计算结果的相对误差如表1所示，由表中数据可以得出如下结论:

(1)两种算法的计算结果基本接近，说明线性化后，绝对位移直接求解的虚拟激励法在一定程度上可以代替传统随机振动法来研究结构的抗震性能，此方法的优越性具有如下几点:① 计算时不需要将绝对位移分解成拟静力位移和动态相对位移两部分;②构造虚拟激励进行简谐响应分析时不需要计算拟静模态矩阵A，简单易行;③ 其实质并没有改变传统虚拟激励法的基本原理，其计算效率也和传统虚拟激励法相当。

(2)绝对位移法相比于随机振动法，加速度响应功率谱密度的误差最小，46号节点最大误差仅为1.15%，154号节点最大误差仅为1.37%，造成这一现象的主要原因是，在模型的前期分析时，输入的激励为加速度功率谱密度，所以在经过一系列的计算后，其对应的加速度响应功率谱密度是最接近实际情况的，而位移、速度响应功率谱密度经过了比加速度响应谱密度更多的计算步骤，使其误差累积，所以46号节点位移功率谱密度最大误差达到11.1%，154号节点位移功率谱密度最大误差达到9.14%。

表1 两种算法的误差对比表Tab.1 Contrast of two algorithms'error

3.4 绝对位移法、时程法及谱分析的对比分析

目前抗振分析中，除上述提出的随机振动法和谐响应分析法之外，谱分析和动力时程法也是很重要的研究方法，动力时程分析法其实质为瞬态分析的Full法，可以考虑各种非线形因素，因此对于本文研究的算例，可以跳过线性化过程直接对其进行动力时程分析，计算时考虑隔阵支座，结构为非正交阻尼体系，输入的人工波按上述绝对位移法所采用的条件生成，地震作用采用双向水平一致地震激励，按照抗震规范，次方向的地震加速度乘以0.85的系数。

为了将上述时程分析的非线性结果与线性结果做对比分析，此处采用了文献［7］提出的GB50011-2001修正反应谱模型进行谱分析，仍采用Rayleigh阻尼的形式，其它条件同上［16］。

图5为主跨跨中节点和背跨跨中节点的位移时程图，通过对比，可以发现如下规律:

(1)由于谱分析是在线弹性范围内研究斜拉桥的位移响应，因此较之于动力时程法及线性化处理后的绝对位移法，其位移响应值均偏小，相比于位移响应最大的动力时程法，最大偏差达到50%以上，说明在研究结构的抗震性能时，必须考虑结构的非线性，否则会引起较大误差，使计算结果偏离真实值。

(2)计入非线性后的绝对位移法与动力时程法的计算结果非常接近，对于46号节点X向位移最大误差仅为7.8%，对于154号节点Y向最大误差为7.3%，并且通过研究发现，其它主梁、主塔及斜拉索节点的位移响应也有类似规律，说明线性化后的绝对位移法可以充分考虑结构的非线性，可以作为抗震设计的一种行之有效的方法。

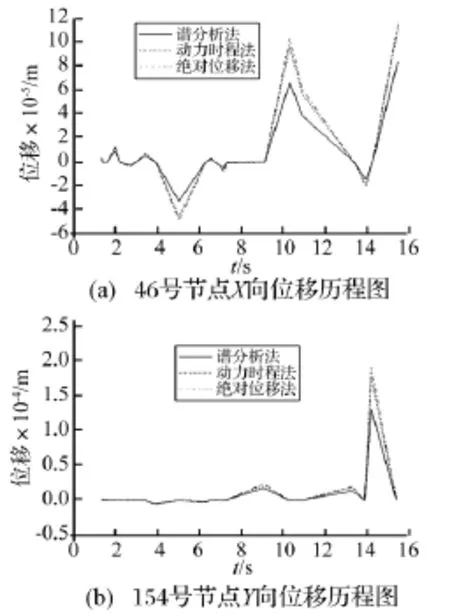
图5 节点位移对比图Fig.5 Contrast of node displacement

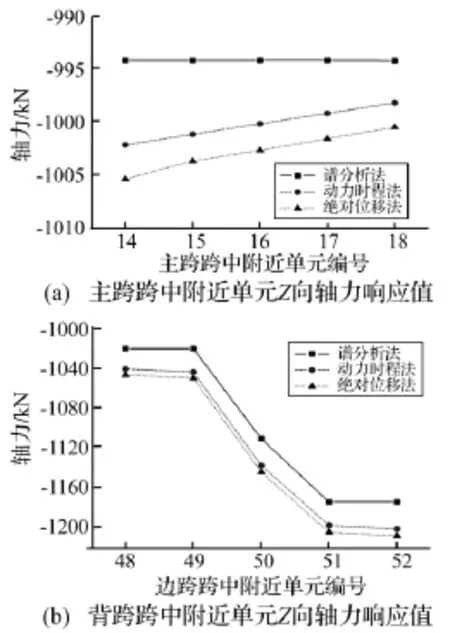
图6 轴力响应对比图Fig.6 Contrast of axial force response

图6为三种计算方法在一致地震动作用下典型单元的Z向轴力响应均值对比图，从图中可以看出，线性化后的绝对位移法求得的单元轴力响应值最大，并且与动力时程法计算出的单元轴力值基本相同，最大误差仅为0.23%(主跨跨中附近的单元)，对于谱分析，其Z向轴力响应值均偏小，较之于动力时程法，最大误差达到8%，说明非线性对结构抗震性能有一定得影响，在桥梁结构的抗震分析中必须加以考虑。

4 结论

(1)相比于传统的虚拟激励法，基于统计线性化的绝对位移直接求解的虚拟激励法，首先充分考虑了结构的非线性，使其抗震分析结果更加接近于真实情况;其次在计算时，不需要将绝对位移分解成拟静力位移和动态相对位移，在构造虚拟激励进行简谐响应分析时，不需要计算拟静模态矩阵，可以在一般的通用有限元分析软件中直接应用，方便虚拟激励法在实际工程中的应用。

(2)体系线性化后，绝对位移法和随机振动法计算得到的节点响应功率谱密度基本相同，说明绝对位移法的正确性，并且计算时输出的响应功率谱密度的精确性依赖于所输入的激励的类型。

(3)相比于动力时程法及线性化处理后的绝对位移法，谱分析没有考虑结构的非线性，其节点位移响应值和单元轴力响应值均偏小，说明非线性对结构的抗震性能有较大影响，在桥梁结构的抗震分析中必须加以考虑。

(4)线性化后的绝对位移法与动力时程法计算出的节点位移响应值和单元轴力响应值基本一致，说明基于统计线性化的绝对位移直接求解的虚拟激励法与动力时程法一样，可以有效地分析和研究非线性体系的抗震性能，唯一要加以区别的是，采用绝对位移法进行谐响应分析时是以频率为间隔输入所需的激励，而动力时程法是以时间为间隔建立地震波数据，但其实质是相同的。

(5)基于统计线性化的绝对位移直接求解的虚拟激励法突破了随机振动计算效率低的瓶颈，并且比常规的反应谱法更精确;其计算时间仅为动力时程法的0.38倍(以本文所提算例为研究对象)，而且动力时程法的计算结果过分依赖所选取的加速度时间历程曲线，要使用许多条地震记录曲线分别计算后再做统计平均，因此本文所提方法比动力时程法更高效，可广泛应用于跨度较大，结构较复杂的桥梁体系的抗震分析中。

［1］林家浩，张亚辉.随机振动的虚拟激励法［M］.北京:科学出版社，2004.

［2］Ernesto H Z，Vanmarcke E H.Seismic random-vibration analysis of multisupport-structural systems［J］.Journal of Engineering Mechanics，1994，120(5):1107-1128.

［3］Abdullateef M A，Ashraf A.An efficient multi-point supportmotion random vibration analysis technique［J］.Computers ＆Structures，2002，80(8):1689-1697.

［4］Lin J H，Zhang Y H，Li Q S，et al.Seismic spatial effects for long-span bridges，using the pseudo excitation method ［J］.Engineering Structures，2004，26(9):1207-1216.

［5］Leper P，Ide I M，Paultre P.Multiple-support seismic analysis of large structures［J］.Computers＆ Structures，1990，36(6):1153-1158.

［6］张笈玮.考虑地震空间效应的大跨度空间结构抗震分析与设计方法［D］.天津:天津大学，2008.

［7］江 洋.大跨建筑结构多点输入地震响应计算与抗震设计方法研究［D］.北京:清华大学，2010.

［8］汪梦甫.非比例阻尼线性体系平稳随机地震响应计算的虚拟激励法［J］.计算力学学报，2008，25(1):94-99.

WANG Meng-pu.Pseudo-excitation method for stationary random responses of non-proportionally damped MDOF systems［J］.Chinese Journal of Computational Mechanics，2008，25(1):94-99.

［9］唐国梁，姚昌仁.统计线性化方法及其计算机数值解［J］.北京工业学院学报，1986，1(1):142-152.

TANG Guo-liang，YAO Chang-ren.Statistical linearization technique and its computer numerical solution［J］.Journal of Beijing University of Technology，1986，1(1):142-152.

［10］林建龙，卢翰庭.统计线性化方法在大型货车垂向振动分析中的应用［J］.铁道学报，1990，12(3):1-7.

LIN Jian-long，LU Han-ting.Research on application of the statistical linearization technique to analyzing the vertical vibration response of freight cars［J］.Journal of the China Railway Society，1990，12(3):1-7.

［11］潘家强，多自由度非线性振动系统的统计线性化简化方程［J］.浙江大学学报，1983，1(3):90-99.

PAN Jia-qiang，Simplified statistical linearization equations of discrete nonlinear systems［J］.Journal of Zhejiang University，1983，1(3):90-99.

［12］ Iwan W D，Yang I M.Application of statistical linearization technique to nonlinear multidegree-of-freedom systems［J］.Transaction of the ASME-Journal of Applied Mechanics，1972，39(2):545-550.

［13］李永华，李思明.绝对位移直接求解的虚拟激励法［J］.振动与冲击，2009，28(10):185-190.

LI Yong-hua，LI Si-ming.Pseudo excitation method based on solving absolute displacement［J］.Journal of Vibration and Shock，2009，28(10):185-190.

［14］GB50011-2001.建筑抗震设计规范［S］.北京:中国建筑工业出版社，2001.

GB50011-2001.Code for Seismic Design of Buildings［S］.Beijing:China Architecture ＆ Building Press，2001.

［15］石永久，江 洋，王元清.直接求解法在结构多点输入地震响应计算中的应用与改进［J］.工程力学，2011，28(1):75-81.

SHI Yong-jiu，WANG Yang，WANG Yuan-qing.Application and improvement of direct solving method in seismic response analysis of structures under multi-support excitations［J］.Journal of Engineering Mechanics，2011，28(1):75-81.

［16］ Kiureghian A D，Neuenhofer A.Response spectrum method for multi-support seismic excitations［J］.Earthquake Engineering＆ Structural Dynamics，1992，21(8):713-740.