粒子滤波参数估计方法在齿轮箱剩余寿命预测中的应用研究

孙 磊，贾云献，蔡丽影，张星辉

(1.军械工程学院装备指挥与管理系，石家庄 050003;2.石家庄军械技术研究所，石家庄 0500031)

设备剩余寿命预测是实现基于状态维修(CBM)的关键技术之一，准确的剩余寿命预测对维修决策的优化起着重要的指导作用，因而受到了广泛地关注和研究。特别地，当设备的未来状态能够准确预测后，对确定其维修检测间隔期和开展以可靠性为中心的维修(RCM)将大为方便［1］。而且现代维修策略的制定越来越依赖于设备当前状态而不是按照维修计划按部就班，这就需要准确预测出设备未来退化的发展趋势。因此，对设备进行早期故障识别并预测其剩余寿命(RUL)显得尤为重要。

目前，很多学者通过建立复杂的系统退化模型来预测设备的剩余寿命，在这些模型的基础上制定维修策略［2-5］。例如，Vlok等［6］将状态监测值作为协变量，用于比例风险模型(PHM)预测;Kopnov，Pulkkinen等［7，8］假定完全监测情况下，建立随机退化过程模型来制定最优维修策略。在实际应用中，因为设备的退化状态很难被直接监测到，对设备的剩余寿命预测往往比较困难，而且监测值也常常被噪声所“污染”。因此，需要建立基于噪声量测序列的系统退化模型，然后通过设备量测值对其内在状态值进行估计，进而计算设备剩余寿命的预测值。

贝叶斯理论非常适合解决这类状态估计问题，它可以将过程监测数据(一般是序贯观测值)作为先验信息，对设备未来的状态值进行递推估计。典型的贝叶斯估计方法是卡尔曼滤波(KF)，它可以求得高斯噪音下，线性状态空间模型的最优解［9］。然而在实际应用中，绝大多数动态系统往往是非线性的，量测噪声也往往是非高斯的。为解决上述问题，各种改进算法和新算法相继提出，例如，通过扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)解决非线性高斯系统的状态估计问题［10］。近年来，随着计算技术和硬件存储技术的快速发展，序贯蒙特卡罗(SMC)方法，也叫粒子滤波(PF)算法，被越来越多地用于估计非线性非高斯条件下的系统状态。文献［11］将它应用于马尔科夫跳变线性系统，产生了很好的效果。

近年来，基于PF理论的故障诊断研究已经得到了越来越多的关注，但是基于PF的剩余寿命预测问题研究的还相对较少。为此本文结合粒子滤波对非线性非高斯系统的处理能力，提出了一套基于粒子滤波理论的设备剩余寿命预测框架。用非线性状态空间模型(SSM)来表示系统的故障演化过程，通过粒子滤波算法预测出系统状态的概率密度函数(PDF)。本文所提出的方法不仅能够提供设备剩余寿命的预测结果，还能够计算出结果的期望值和置信区间。另一方面，PF算法的研究仍处于发展阶段，在实际系统寿命预测中的应用还不成熟，绝大部分都是用于仿真领域，即人工时间序列模型产生输入数据［12］。针对上述问题，我们对PF算法在工程实际中的预测应用开展了实验研究。

1 理论基础

1.1 问题的提出

基于状态空间模型的系统剩余寿命预测基本原理，是根据系统已知的先验信息得到的未知状态的先验分布，结合观测数据，来估计系统的后验分布及其剩余寿命，如图1所示。

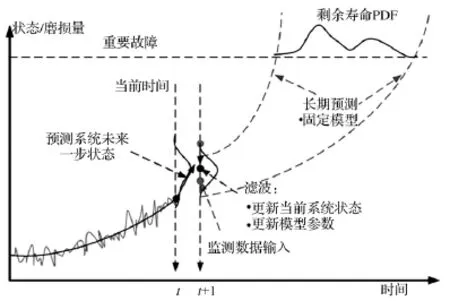
图1 基于状态空间模型的设备RUL预测Fig.1 Concept of dynamic model-based prognostics

一般地，用下面的状态方程来描述系统模型及其状态向量的演化过程:

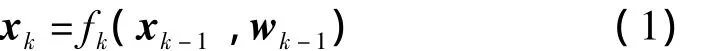
其中，fk∶Rnx×Rnw→Rnx是非线性函数，时间步长为tk=kΔt，{wk，k∈N}是已知分布形式的状态噪声向量序列。状态向量序列{xk，k∈N}服从一阶马尔科夫过程。假设系统初始状态p(x0)已知，状态转移概率p(xk|xk-1)由状态方程(1)和分布类型已知的噪声向量wk定义。

系统的量测方程可由连续观测值tk的观测序列{zk，k∈N}来描述:

其中，hk∶Rnx×Rnv→Rnx是给定的非线性函数，{vk，k∈N}是已知分布形式的量测噪声向量序列。并且，量测向量序列{zk，k∈N}状态独立于状态过程{xk，k∈N}。也就是说已知状态xk时刻t，量测值zk的概率值不依赖于前一时刻的量测序列z0∶k-1=(z0，…，zk-1)。p(zk|xk，z0∶k-1)=p(zk|xk)可由量测方程(2)和噪声向量vk确定。

1.2 传统的比例风险剩余寿命预测模型

比例风险模型(PHM)作为一种剩余寿命预测方法，首先由Cox在1972年提出，并很快成为一种统计数据分析工具［13］。该模型综合考虑设备运行的寿命信息和各种设备状态信息，从而有效地将状态信息用于设备可靠性分析及剩余寿命预测，其基本形式如下:

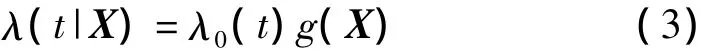
其中，λ0(t)和g(X)都可能含未知参数，λ0(t)可以理解为g(X)=1下的标准故障率函数。由于威布尔分布可作为许多类型设备(如真空管，滚珠轴承和电器的绝缘材料等)的寿命分布模型，因此下面主要研究Weibull-PHM剩余寿命预测模型。

Weibull-PHM的故障率函数定义如下［13］:

相应的可靠度函数为

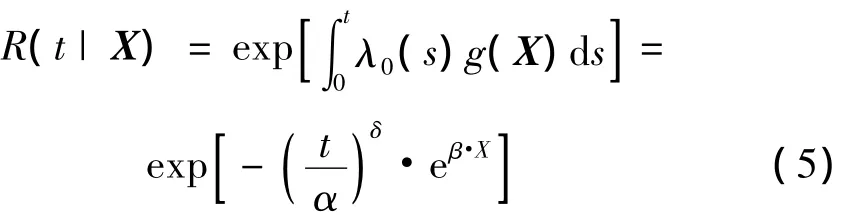
则平均剩余寿命为

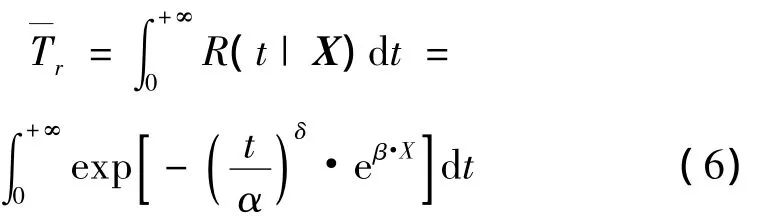
其中，X为设备状态向量，X=(x1，x2，…，xp)';λ(t|X)为设备在状态X的故障率;α、δ为威布尔分布中的尺度参数和形状参数;X是p维状态向量，反映设备的状态信息;β为与X相对应的变量系数，由上述公式可以看出，只要求得参数α、δ和β的值，即可确定Weibull-PHM的具体形式，模型参数用极大似然估计求解即可。

1.3 贝叶斯递归和粒子滤波

根据1.1节，我们想要得到的结果是后验概率分布p(xk|z0，k)，在贝叶斯框架下，已知k-1时刻的概率分布p(xk-1|z0，k-1)，根据系统状态方程(1)来预测系统状态xk先验概率分布，由Chapman-Kolmogorov方程得:

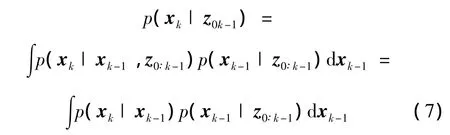
k时刻收集到新的观测值zk，根据贝叶斯准则更新系统状态的后验分布，从而得到当前系统状态xk的后验概率分布:

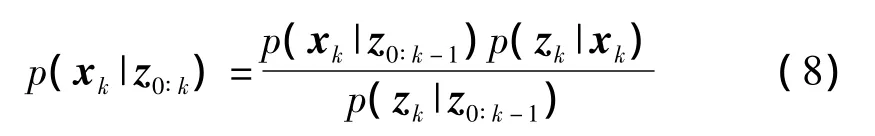
其中的常数项:

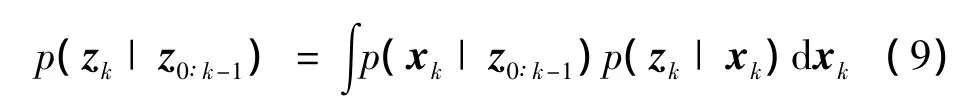
递推公式(7)和公式(8)构成了贝叶斯递归求解的基础。然而，除了极少数情况，包括线性高斯状态空间模型(卡尔曼滤波)和有限状态空间隐马尔科夫链(Wohnam滤波)，用解析方法很难求解上述分布，因为计算需要大量运算和高维积分运算。

这就需要其它有效求解方法——蒙特卡罗采样。接下来，本文只分析蒙特卡罗方法的基本步骤，详细推导参考文献［14-16］。

一般来说，已知量测向量z0;k，系统整个状态序列x0;k的后验分布可以写成下述形式:

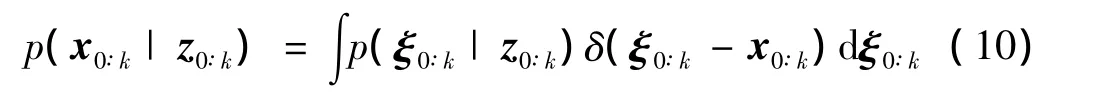
这里，δ(·)是狄拉克函数。假设系统真实后验概率p(x0∶k|z0∶k)已知，且能被采样，则公式(10)可以由下式估计:

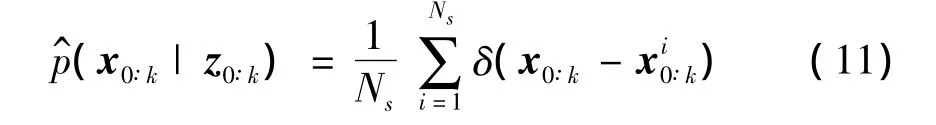
其中，，i=1，2，…，Ns是从p(x0∶k|z0∶k)采样得到的独立随机样本集。

实际上，由于p(x0∶k|z0∶k)可能是多变量、非标准的，通常很难写成解析分布函数的组合形式，抽样过程比较困难。为了克服这个问题，可以借助重要性函数抽样。所谓重要性函数就是指概率分布与p(x0∶k|z0∶k)相同，概率密度分布 π(x0∶k|z0∶k)已知，而且容易从中抽样的分布函数，则公式(10)可以变换为:

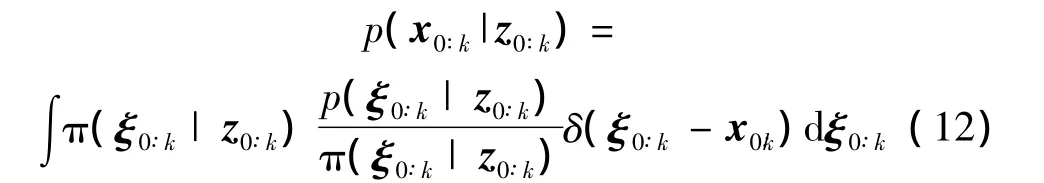
其估计式为:

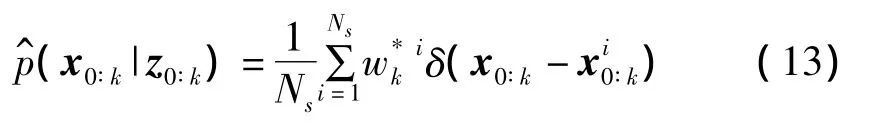
其中，

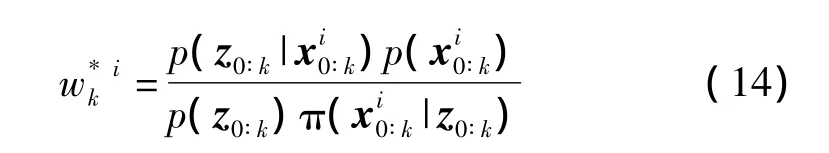
是系统状态序列，i=1，2，…，Ns的权重，它可以通过 π(|z0∶k)采样得到;p(z0∶k|)是观测序列的似然值。实际计算中，该权重很难求解，它需要知道p(z0∶k)= ∫p(z0∶k|x0∶k)p(x0∶k)dx0∶k，但上式很难表示为闭合形式进行解析求解。为了解决这个问题，后验分布p(x0∶k|z0∶k)可以由下式计算得到:

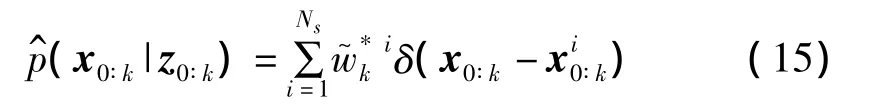
其中，

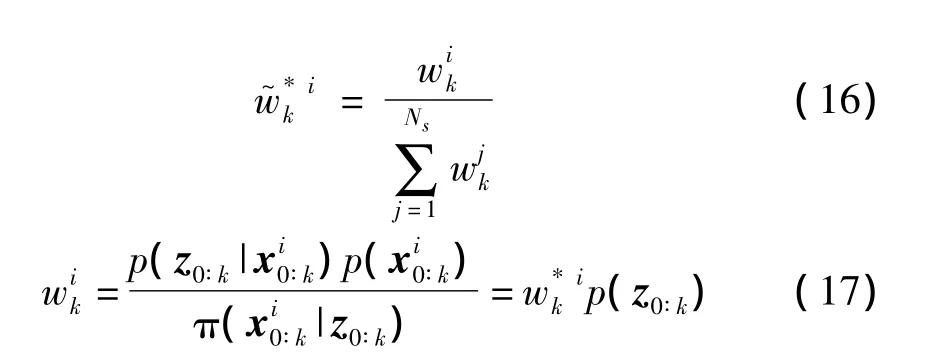
这样，根据系统前k-1时刻状态的分布p(x0∶k-1|z0∶k-1)来估计k时刻状态的分布p(x0∶k|z0∶k)。从而，再根据贝叶斯滤波理论，由公式(8)递推得到p(x0∶k|z0∶k):

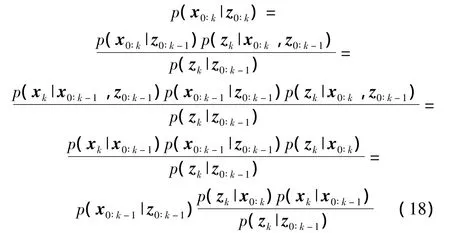
其中，推导过程中再次用到了系统状态方程(1)符合一阶马尔科夫过程这个假设，在系统状态序列已知的情况下，量测方程(2)是条件独立的。则重要性函数可以选取如下:

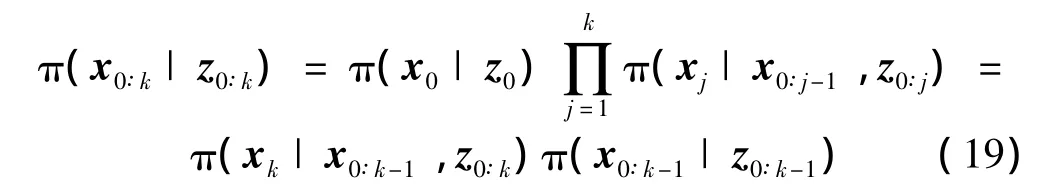
然后，可以得到非归一化的和权值递推公式如下:

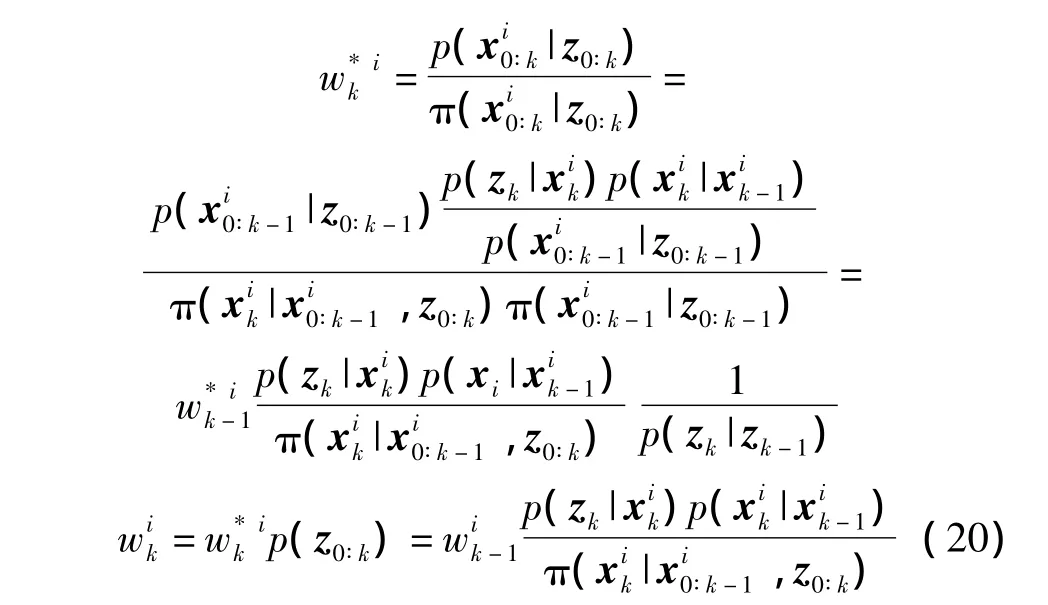
重要性函数的选取是一个非常关键的问题，选取原则之一就是使得重要性权值的方差最小。文献［16］指出，选 择 π (xk|x0∶k-1，z0∶k)=p(xk|x0∶k-1，z0∶k)可以满足重要性权值的方程最小原则，但是这种选择方法在实际中往往比较难以实现。从实际应用角度来讲，多数文献普遍选择采用 π(xk|x0∶k-1，z0∶k)=p(xk|xk-1)，这种方法尽管不是最优方法，但是较容易实现。

然而，重采样算法仍然存在严重的局限:在迭代很少几步之后，重要性权值有可能集中到少数粒子上。这使得大量的更新运算对最后的估计几乎不起作用。通常，在迭代几步之后，除了一个粒子权重外，其余粒子的权重都几乎趋向于零。

为了避免这种退化，可以采用 bootstrap采样技术［16］。对离散估计p(x0∶k|z0∶k)进行重采样Ns次，得到一系列粒子{xi*k，i=1，2，…，Ns}。本文采用了序贯重要性重采样算法(SIRs)，具体过程如下:

归一化权重

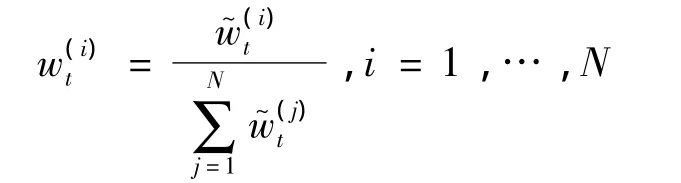
重采样

如果重采样，则根据权重选择N个粒子序列

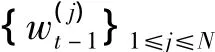
否则，

End

其重要性函数的权重为:

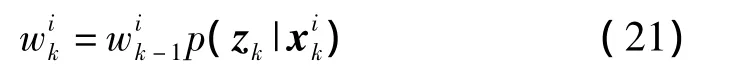
在每一步迭代过程都要进行重采样wik-1=1/Ns，经过归一化和更新后的权重等于量测量的似然值，即:

2 基于粒子滤波的剩余寿命预测方法

机械设备的振动信号可以作为描述其退化状态的指标，为了准确预测设备的退化趋势及其剩余寿命，本文提出了基于设备振动信号和粒子滤波参数估计的预测算法，见图2所示。具体包括以下四步:

步骤一:(数据采集)首先通过振动传感器采集机械设备的原始信号，包括其从正常状态到发生故障的全寿命数据。

步骤二:(特征提取)提取反映设备退化趋势的特征指标，本文选用的是特定频带能量和机械设备的磨损量。

步骤三:(预测和滤波)通过逐步采样，应用粒子滤波算法，计算粒子的重要性权重，然后重采样技术，实现设备的寿命预测。

步骤四:(效果评估)为了确定所提方法的有效性和准确性，首先对预测结果是否落于其95%置信区间进行分析，然后提出预测效果评估指标和相应计算方法，进一步对预测的结果进行效果评估。

为了对上述预测算法的效果进行综合定量的评估，本文选用均方根误差(RMSE)、平均绝对误差(MAE)和方差绝对误差(VAE)作为绝对误差指标;用平均相对误差(MARE)和方差相对误差(VRE)作为相对误差指标。它们的计算公式如下:

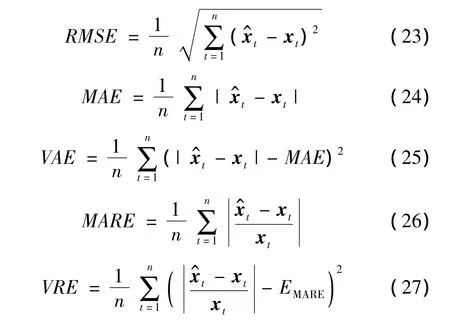
其中，xt表示状态真实值表示状态预测值，上述指标值越小，表示预测的精度越高。

3 应用案例分析:齿轮箱全寿命实验及其剩余寿命预测

3.1 实验设置

齿轮箱由于其结构紧凑、传动精确等优点，广泛应用于设备传动系统中，由于其工作环境恶劣等原因，齿轮箱容易出现故障，因此本文选择齿轮箱作为实验和研究对象，对其进行剩余寿命预测，讨论本文所提方法的实际应用问题。

实验设备和实验所用齿轮箱的结构如图3所示，传感器测点布置如图4所示。动力源为电磁调速电机，型号YCT180-4A，磁粉制动器为齿轮箱提供载荷，型号FZ200.K/F型风冷磁粉制动器。实验工况，扭矩为额定负载的2～2.5倍，目的是为了减少实验时间。实验所用齿轮箱主要参数见表1。

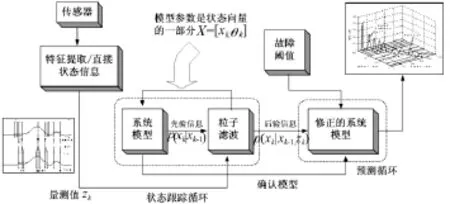
图2 粒子滤波预测算法流程图Fig.2 Flowchart of particle filter algorithm for prognosis

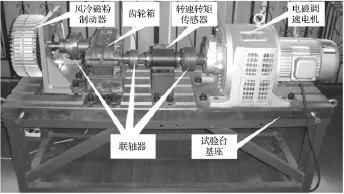
图3 实验台和齿轮箱结构示意图Fig.3 Sketch map of the test-bed and gearbox structure

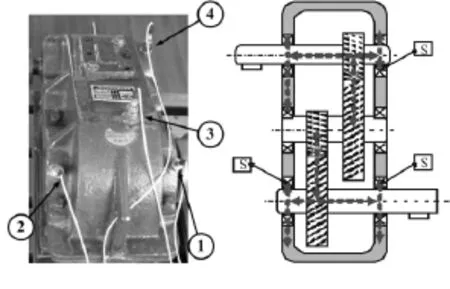
图4 齿轮箱振动传感器安置位置Fig.4 Accelerometers mounting

表1 齿轮箱主要参数Tab.1 Prime parameters of the gearbox

实验齿轮箱为本实验的核心部分(图4)，它是一种二级斜齿轮箱，额定传输功率为0.75 kW;在箱体的不同部位上共装有4个振动加速度传感器，能够通过数据采集系统同时采集4路不同部位的振动信号。通过实验发现，本次被测齿轮箱工作约450小时后，主要故障形式是齿轮齿面的严重磨损，实验结果如图5所示。

图5 齿轮实验前后对Fig.5 Comparison of gear before and after experiment

3.2 实验数据采集和特征提取

实验过程中对齿轮箱振动信号进行采集，采样频率为20 k，采集长度为40 k，每小时采样1次，累计采样448 h。

对采集到的数据，利用小波包频带能量提取方法［17］，获取不同时刻振动信号特定频带能量(3～4.5 kHz，通过观测，该频带的振动信号能量随工作时间逐渐增大，趋势较为明显，反映齿轮箱健康状态的指标较为理想){Ei;i=1，2，…，448}作为观测特征值，如图6所示。同时对轮齿磨损量进行不完全数据采集，即仅对部分运行时刻的磨损状态进行检测，所获得的磨损数据如表2。

表2 不同检测时间轮齿磨损量Tab.2 The wear of gear teeth at different inspections

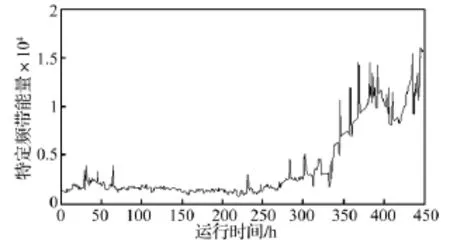
图6 齿轮箱振动信号特定频带能量Fig.6 Special band energy of vibration

3.3 基于PHM的齿轮箱剩余寿命预测

为了克服模型在小样本且存在异常数据条件下预测精度较差的缺陷，需要选取一定的方法识别状态信息样本中的异常数据，以提高PHM的预测精度。本文采用支持限量机(SVM)算法，对状态信息样本中的异常数据进行识别及分离。

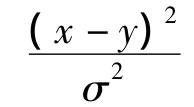
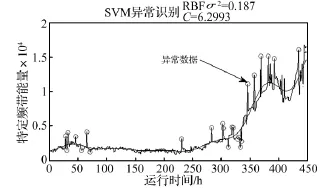
图7 异常数据识别结果Fig.7 The results of abnormal data detection

利用SVM对样本进行处理及平滑后，进一步利用PHM进行齿轮箱剩余寿命预测。通过极大似然算法可获得最有参数为:α =438.9，δ=4.216，β =2.567 ×10-5，则齿轮箱的故障率函数为

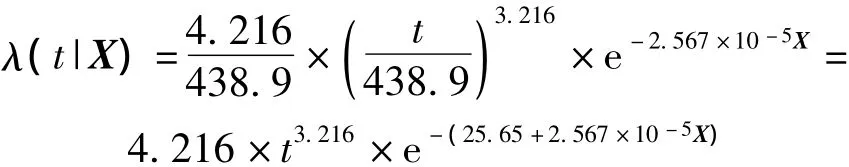
通过计算，可得齿轮箱在不同时刻预测的平均剩余寿命，表3为不同检测时间的剩余寿命预测结果。

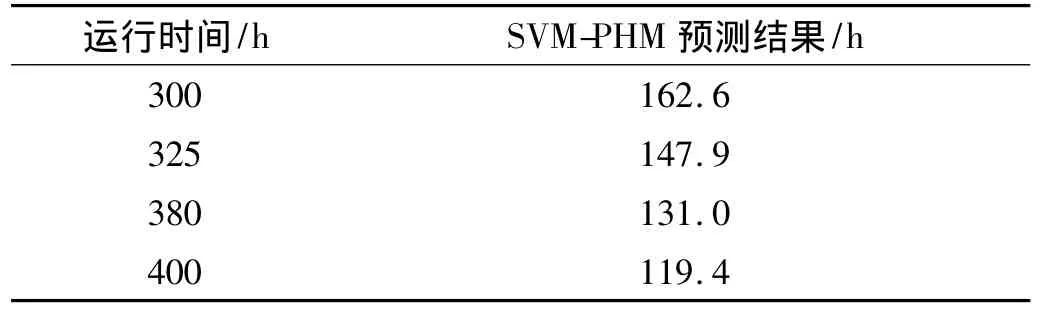
表3 齿轮箱剩余寿命Tab.3 The remaining useful life of the gearbox

3.4 基于PF的齿轮箱剩余寿命预测

基于PF的齿轮箱剩余寿命预测模型与传统PHM不同，其训练样本综合采用特定频带能量E和磨损量wl。利用PF对齿轮箱轮齿磨损过程进行建模。由于Gamma过程具有平稳、独立增量等退化建模所需的所有属性，被认为是描述产品退化过程的首选方法［18］，磨损量演化的状态空间模型如下:

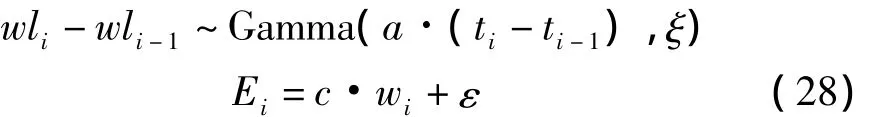
取448 h的磨损量0.3 mm为故障阈值WLf，ε～(0，σ)为观测误差。为便于计算，取a(0)的初始值为1，分别可得初始参数参数ξ(0)=2 105、c(0)=48 744和σ(0)=968.7。令Wu表示所获得的第u个磨损量观测值，相应的监测时间为tu，通过PF方法可计算模型参数，其收敛过程如图8所示。

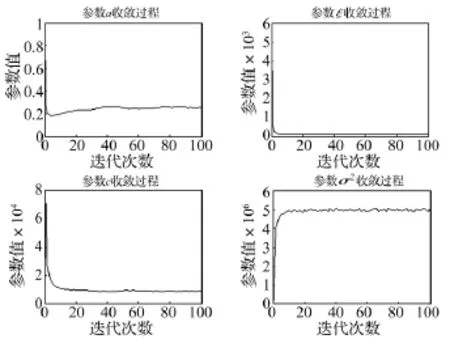
图8 参数收敛过程Fig.8 Convergence of the parameters

由于参数求解过程中，滤波粒子通过先验分布随机生成，导致每次参数求解结果具有一定的随机性，因此进行1 000次重复参数求解后可得各参数的分布图及参数均值和标准差，具体结果见表4。

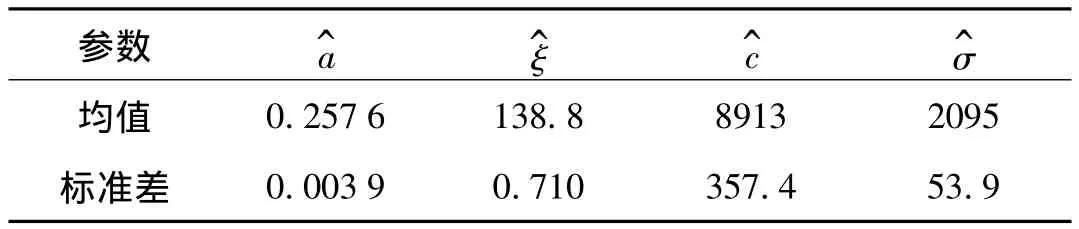
表4 参数评估结果Tab.4 The results of parameter estimation

获得模型参数后，可对不同时刻的磨损情况进行评估，利用状态方程可实现对未来裂纹概率密度的预测，预测公式为:

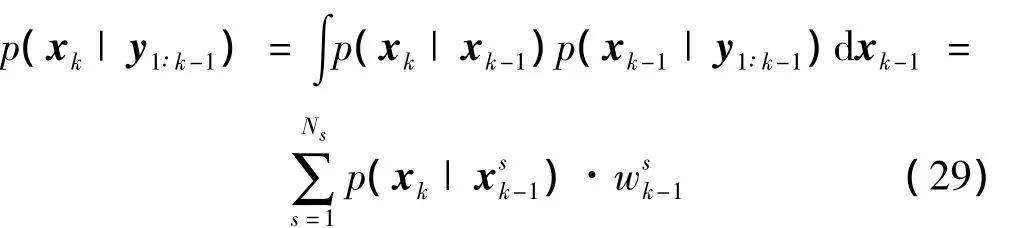
其中，p(xk|)为xk在粒子条件下的先验概率论，为粒子所对应的权值，粒子集{，由粒子滤波算法获得。则通过式(29)，可实现对齿轮箱磨损量的预测，预测结果如图9所示。

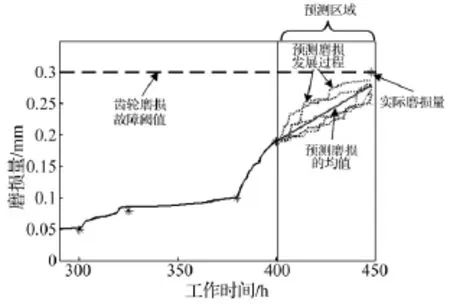
图9 磨损量预测结果Fig.9 The prediction results of wear

通过计算，分别得到400 h时的齿轮箱剩余寿命累积分布函数、概率密度函数和剩余寿命(如图10，其中实际剩余寿命为48 h，预测值为60.7 h)。

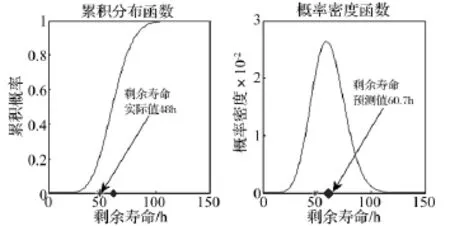
图10 400 h时的剩余寿命累积分布及概率密度函数Fig.10 The CDF and PDF of RUL at 400 h

采用同样的方法，得到不同时刻的振动检测序列后，确定相应的模型参数，表5为不同时刻测模型参数。

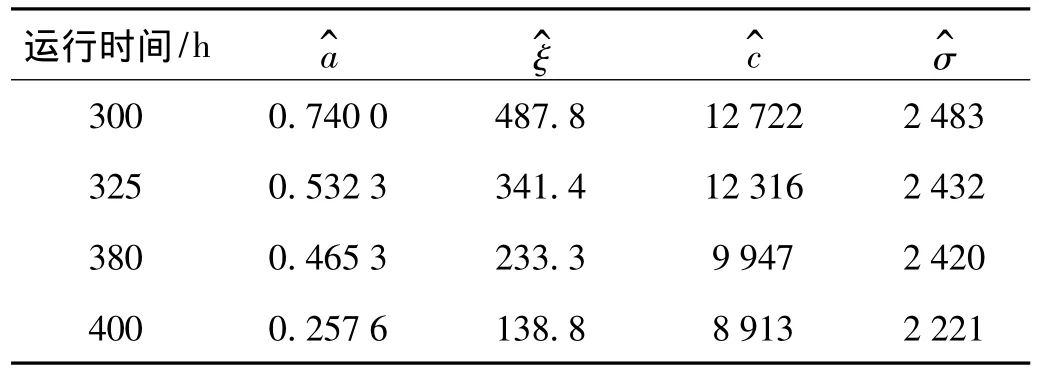
表5 不同检测时刻的模型参数Tab.5 Estimated parameters at different inspection time

获得不同时刻模型参数后，可计算得到剩余寿命的概率密度函数和平均剩余寿命，如图11所示。表6为不同时刻的剩余寿命预测结果及95%的置信区间。根据公式(23)～(27)对预测的结果进行效果评估(见表7)。

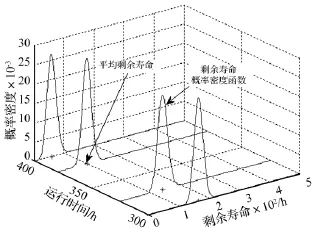
图11 不同检测时刻剩余寿命概率密度函数和均值Fig.11 Probability distribution function and mean of RUL at different inspection time

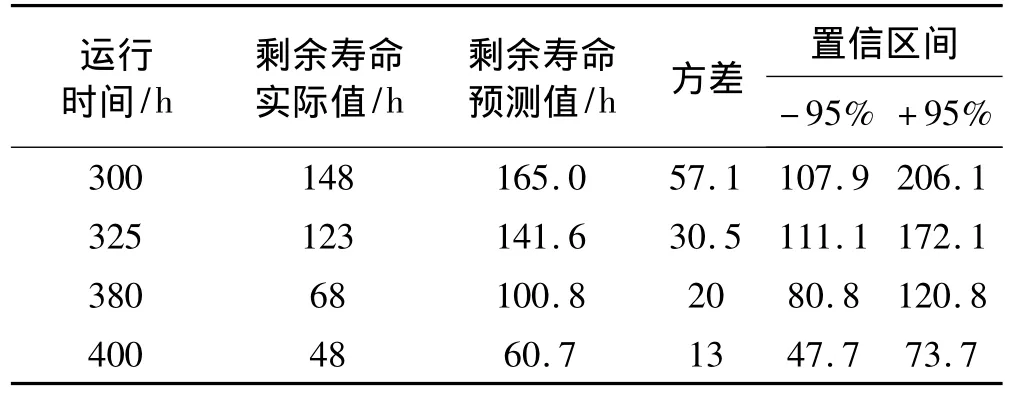
表6 剩余寿命预测值及置信区间Tab.6 Mean value and 95%confidence interval of RUL

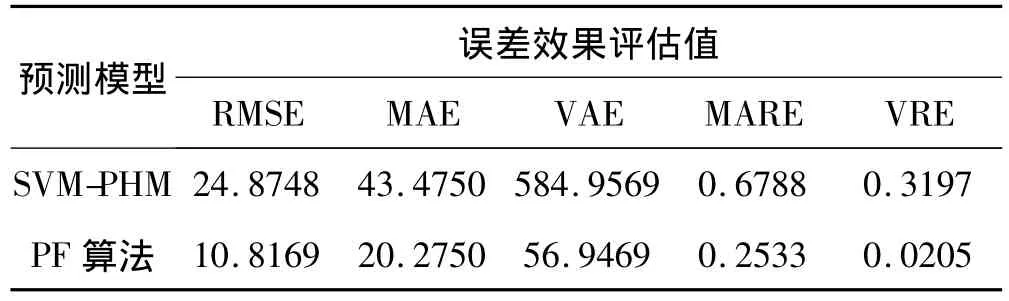
表7 剩余寿命预测效果评估结果Tab.7 Performance evaluation results of RUL prediction

3.5 结果分析

表3和表6分别给出了两种剩余寿命预测方法的预测结果。从表6可知，齿轮箱实际剩余寿命均落于置信度为0.95的置信区间之内，因此基于PF的剩余寿命预测结果具有一定的合理性。表7给出了两种方法RUL预测效果评估结果，从上述5个指标对比可以看出，基于PF的剩余寿命预测无论是在预测的准确度还是精确度方面均较PHM有明显优势。这主要是由于基于PF的剩余寿命预测时综合考虑了磨损量和振动特征值，使模型能够更为准确的反映齿轮箱的磨损过程;而PHM单纯采用振动特征进行剩余寿命预测，由于振动特征并不能完全准确地反映齿轮磨损状态，因此预测结果较差。但PHM较基于PF的剩余寿命预测来说，模型结构比较简单，计算复杂度较低，模型求解过程更为容易。

4 结论

本文针对非线性系统剩余寿命预测问题，提出了基于粒子滤波算法的剩余寿命预测框架，并根据系统的状态监测数据，结合粒子滤波算法，提出了剩余寿命预测方法，针对预测效果评估问题，进行了准确性和精确性验证。最后通过齿轮箱全寿命实验进行了实例分析，结果表明，与传统的PHM预测方法进行对比分析，基于粒子滤波模型的剩余寿命预测方法更加有效和准确。

本文的研究结论为复杂噪声条件下非高斯非线性系统的剩余寿命预测提供了一种可行的解决方法，具有一定的普适性。为增强该方法实际应用的实时性，结合Rao-blackwellized进行算法简化研究和实时预测研究;以及设备多故障模式条件下的故障追踪和预测问题，将做为进一步研究的重点方向。

［1］Marseguerra M， ZioE， PodofilliniL. Condition-based maintenance optimization by means of genetic algorithms and Monte Carlo simulation［J］.Reliability Engineering and System Safety，2002，77:151-65.

［2］ Samanta P K，Vesely W E，Hsu F，et al.Degradation modeling with application to aging and maintenance effectivenessevaluations［R］. NUREG/CR-5612. US Nuclear Regulatory Commission，1991.

［3］Kopnov V A.Optimal degradation process control by twolevel policies［J］.Reliability Engineering and System Safety，1999，66:1-11.

［4］Lam C， Yeh R. Optimal maintenance policies for deteriorating systems under various maintenance strategies［J］.IEEE Trans Reliability，1994，43:423-430.

［5］Hontelez J A M，Burger H H，Wijnmalen D J D.Optimum condition-based maintenance policies for deteriorating systems with partial information［J］.Reliability Engineering and System Safety，1996，51:267-274.

［6］ Vlok P J，Coetzee J L，Banjevic D，et al.An application of vibration monitoring in proportional hazards models for optimal component replacement decisions［J］.Journal of Operational Research Sociaty，2002，53:193-202.

［7］Kopnov V A.Optimal degradation process control by twolevel policies［J］.Reliability Engineering and System Safety，1999，66:1-11.

［8］Pulkkinen U，Uryasev S.Optimal operational strategies for an inspected component［C］.In:Petersen K E，Rasmussen B，editors.Safety and Reliability'92， Proceedings of the European Safety and Reliability Conference'92.London，1992:896-907.

［9］Anderson B D，Moore J B.Optimal filtering［M］.Englewood Cliffs(NJ):Prentice Hall，1979.

［10］ Myotyri E，Pulkkinen U，Simola K.Application of stochastic filtering for lifetime prediction［J］.Reliability Engineering and System Safety，2006，91:200-208.

［11］ Zio E.Parameter identification in degradation modeling by reversible-jump Markov Chain Monte Carlo［J］. IEEE Tranctions on reliability，2009，58(1):123-131.

［12］ Guo D，Wang X，Chen R.New sequential Monte Carlo methods for nonlinear dynamic systems［J］.Statistics and Computing，2005，15:135-147.

［13］ Newby M.Perspective on Weibull proportional hazards models［J］.IEEE Transactions on Reliability，1994，43(2):217-223.

［14］ Orchard M E，Tang L，Goebel K，et al.A novel RSPF approach to prediction of high-risk，low-probability failure event［C］.Annual Conference of the Prognostics and Health Management Society，2009:1-8.

［15］ Cadini F，Zio E.A Monte Carlo method for the model-based estimation of nuclear reactor dynamics［J］.Ann.Nuclear Energy 2007，34(10):773-781.

［16］Doucet A，de Freitas N，Gordon N.Sequential Monte Carlo in practice［M］.New York:Springer-Verlag，2000.

［17］ Hu Q，He Z J.Fault diagnosis of rotating machinery based on improved wavelet package transform and SVMs ensemble［J］.Mechanical Systemsand SignalProcessing， 2007，21:688-705.

［18］ Van Noortwijk J M.A survey of the application of gamma processes in maintenance［J］.Reliability Engineering and System Safety，2009，94:2-21.

［19］ Boser B E，Guyon I M，Vapnik V N.A training algorithm for optimal margin classifiers［C］.The 5th AnnualACM Workshop on Computation Learning Theory，ACM Press，1992:144-152.