铜基面抗拔摩擦摆支座的力学性能研究

李雄彦，薛素铎，潘克君

(1.北京工业大学 建筑工程学院，北京 100124;2.北京市弘都城市规划建筑设计院，北京 100045)

随着振动控制技术的发展，支座隔震技术逐步应用于结构减震设计，建筑结构隔震可分为基础隔震和高位隔震。基础隔震是在基础与上部结构间设置柔性的隔震层或安装隔震支座，高位隔震一般是在屋盖与下部支承结构安装隔震装置。目前常用的隔震装置有橡胶支座和摩擦支座两大类，其基本原理主要是通过隔震层改变结构的动力特性，减少地震动能量的输入和振动，并利用支座耗散部分地震动能量。

摩擦摆隔震系统(FPS)系摩擦类支座，该支座由Zayas等［1-2］在美国加州大学伯克利分校研发成功。FPS隔震消能原理是利用摩擦滑移层延长结构的自振周期，以大幅度减少地震作用产生的结构动力放大效应。同时，FPS滑动面与滑块之间的摩擦可有效消耗地震能量，减少结构地震输入。摩擦摆支座滑动面为不锈钢材料制作的下凹球状表面，与滑动面接触的滑块底面涂有聚四氟乙烯(Teflon)复合摩擦。

美国加州大学地震工程研究中心(EERC)、美国国家地震工程研究中心(NCEER)和加州大学圣地亚哥分校(UCSD)等科研机构对摩擦摆支座进行了大量的性能研究试验，结果表明摩擦摆支座具有稳定的滞回性能和优异的耐久性。Zayas等［3-4］对摩擦摆支座在温度、时间、热运动等影响因素下进行了测试，试验证明摩擦摆支座在动力测试下的有效性和可预测性，其抗压性和稳定性可以防止支座过载，提供可靠的安全机制。Constantinou等［5-8］就滑道内衬Teflon材料的摩擦耐久性和可靠性进行了大量的理论研究和试验研究。试验发现支座的摩擦系数不仅与接触面材料特性有关，还与接触面的压强，滑动速度等有关。

早期摩擦摆多采用基础隔震的方式，主要应用于上部较重的桥梁或建筑结构，该类支座在各荷载工况下一般不会出现拉力。针对可能出现拉力的多层结构，Rousssis等［9-10］开发出了一种双向滑动的抗拔摩擦摆支座。然而，随着隔震技术的发展，摩擦摆支座开始应用于空间结构［11-13］。与桥梁和多高层结构相比，空间结构多采用高位隔震，在屋盖与下部支承结构间安装支座。因此，在风荷载以及竖向地震的作用下，利用摩擦摆支座隔震时，支座的上部盖板和滑块可能会由于受拉而脱离，致使摩擦摆支座失效，抗拔成为亟待解决的问题之一。此外，应用于空间结构的摩擦摆支座一般应具有万向转动能力。

现有的摩擦摆支座的摩擦面一般采用Teflon涂层滑块与不锈钢球面组成摩擦副，由于Teflon的抗压强度远低于不锈钢材料，因此支座的大小与滑块的强度有密切联系。若能采用高强且摩擦系数与Teflon相当的材料替代现有的摩擦副，则有效减小支座的尺寸。

本文针对上述问题，介绍了抗拔型摩擦摆支座的基本构造，将新型的铜基复合材料应用于摩擦摆支座，通过试验测定了新型铜基摩擦摆的摩擦系数和滞回性能，基于试验研究结果，验证了现有摩擦摆支座理论模型的适用性。

1 竖向抗拔摩擦摆支座的构造与力学模型

1.1 支座构造

抗拔型摩擦摆支座由下底座、中间滑块、抗拔挡板、挡块、上部盖板等五部分构成(图1)［14］。滑槽内滑动面上附有自主研发的新型青铜基复合减摩材料，该材料具有摩擦系数小，承载力高的特点。滑块下表面为抛光不锈钢板，采用镀铬处理，以减小滑动面间的摩擦系数。滑块上球面和挡块下球面间的相对转动提供支座的转动能力，滑块在滑槽中的滑动产生水平位移，挡块和抗拔挡板之间的接触实现抗拔。

1.2 支座的理论模型

抗拔型摩擦摆支座在沿球面凹槽滑动时，与传统的摩擦摆支座一样，其基本力学模型可简化为沿圆弧面滑道运动的滑块(图2)，其中滑道半径及滑块底部圆弧面半径均为R，滑块质量为m1。θ表示滑块m1相对于滑道竖向对称轴运动的转角，以逆时针为正，摩擦摆的水平力F平衡方程可表示为:

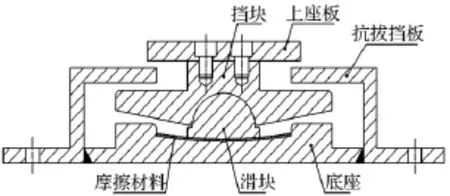
图1 支座构造示意图Fig.1 Sketch of the bearing

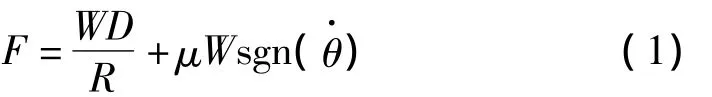
其中:摩擦摆水平位移D=Rsinθ;滑块正压力N=Wcosθ;W为上部结构竖向荷载W=Mg;μ是滑块动摩擦系数，可采用库伦模型;符号函数sgn()可表示为:

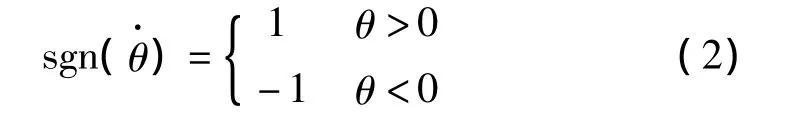
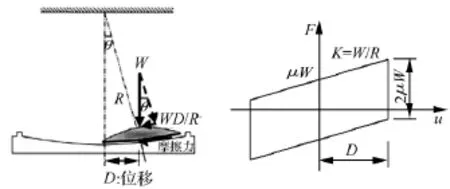
图2 摩擦摆受力模型Fig.2 Mechanical model of FPS

摩擦摆系统的摩擦力能呈非线性，可用等效线性刚度和等效粘滞阻尼来模拟其非线性，基于图2中的滞回模型，可采用美国AASHTO(the American Association of State Highway and Transportation Officials)计算等效线刚度KE和等效粘滞阻尼 ζE［15］:

等效粘滞阻尼系数为:

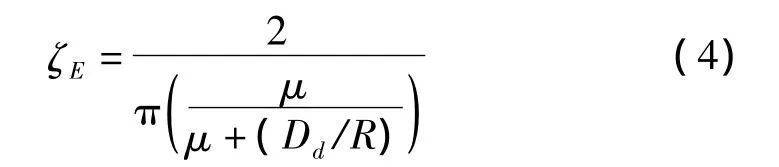
设Keff为隔震系统的等效刚度，KU为与上部结构基本振型相对有效刚度，则:

当上部结构为刚性时，刚度KU=∞，此时Keff=KE。因此，摩擦摆隔震结构的等效自振周期约为:

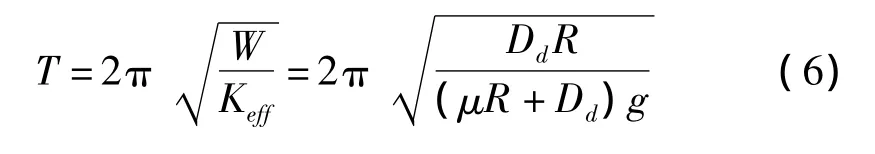
从摩擦摆的力学性能计算公式看出，除几何参数外，摩擦系数对其等效刚度和等效阻尼有重要影响。同时，对于青铜基摩擦副组成的摩擦摆支座，其滞回性能是否具有刚塑性特征是式(3)、(4)成立的前提条件。为了确定摩擦系数和支座的滞回特征，因此需要对支座进行性能试验。

2 竖向抗拔摩擦摆支座的试验研究

2.1 试验模型概况

试验模型选用FPB3000型竖向抗拔摩擦摆支座，支座剖面与实体照片如图3所示。试验支座竖向设计承载力3 000 kN、抗拔承载力600 kN，设计转角为0.06 rad，径向允许位移为+70 mm。支座受力件选用铸钢ZG275-485H、Q235B制造，摩擦材料选用新研发的铜基复合材料，其抗压强度为320 MPa。摩擦材料的金像照片和滑槽实物照片如图4和图5所示。

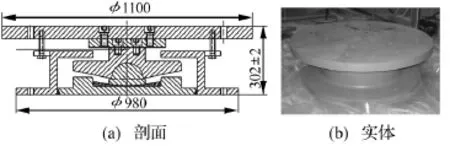
图3 支座试验模型Fig.3 Experimental Bearing

图4 摩擦材料照片Fig.4 Photo of frictional material

图5 滑槽实物照片Fig.5 Photo for the frictional interface

2.2 试验装置简介

试验在4 000 t多功能电液伺服加载系统完成，数据采集采用IMP359551B型静态数据采集系统，采集参数16位，采集频率1Hz。由于试验装置电脑采集的水平位移与实际位移相差较大，存在固有误差，为了弥补装置自身缺陷，在试验过程中增加两个位移传感器，以采集支座水平位移。两个传感器分别布置在支座水平行程的前、后两端，为了使其数值相互修正，减小数据误差，试验装置如图6。

2.3 试验工况

支座性能试验主要测试摩擦系数和滞回性能，测试时竖向分别施加1 000 kN、2 000 kN和3 000 kN的压力;水平向采用位移控制，测试时输入正弦位移曲线，幅值为70 mm，加载频率分别为 0.05 Hz、0.1 Hz和0.2 Hz，试验加载工况如表 1。

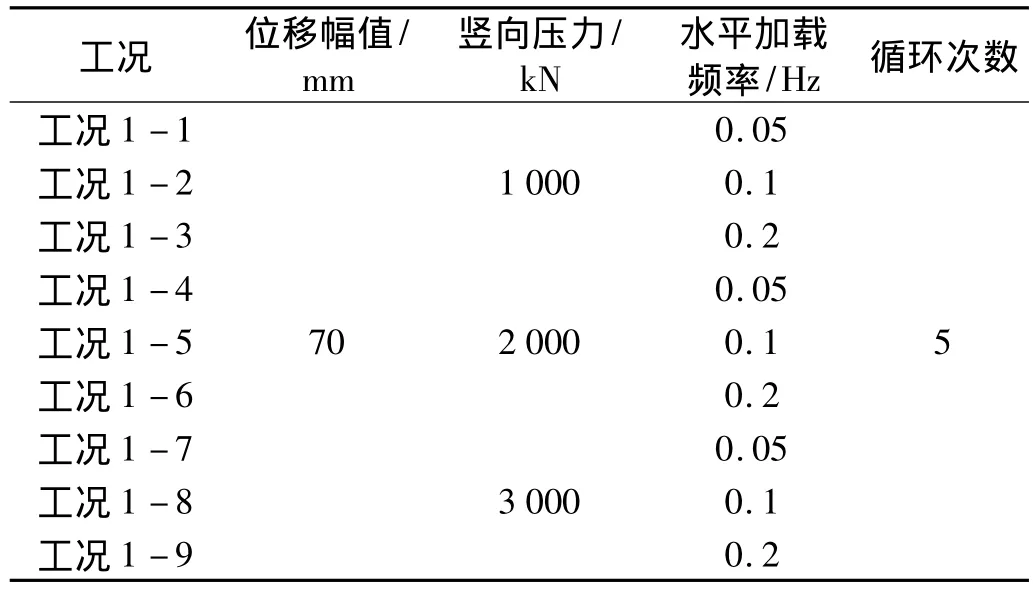
表1 支座性能试验加载方案Tab.1 Experimental Loading Scheme of Hysteretic Property

图6 试验装置简图与照片Fig.6 Experimental set-ups

2.4 试验结果分析

(1)滞回性能测试

图7给出了工况3的水平位移-时间曲线和滞回曲线。图8给出了竖向压力为1 000 kN和2 000 kN条件下不同加载频率的滞回性能对比。

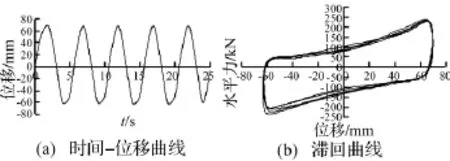
图7 工况3的位移输入与滞回测试结果Fig.7 Displacement input and experimental hysteric loops

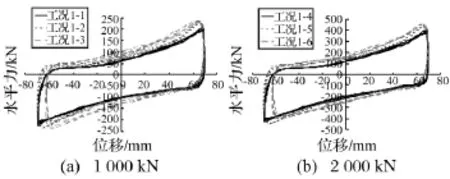
图8 相同压力、不同频率下的滞回曲线对比Fig.8 Comparison of the hysteretic loops with varied input frequency

从图7可看出，支座的滞回曲线饱满，总体呈平行四边形，四边形的两侧边近似竖直，滞回呈刚塑性。由图8可知，支座在相同压力、不同加载频率下滞回性能变化不大，随着加载频率增大，最大位移处水平力略有增大，滞回曲线趋于饱满。在0.2 Hz加载频率下，试验时负向位移采集存在误差，滞回曲线也随之产生差异。

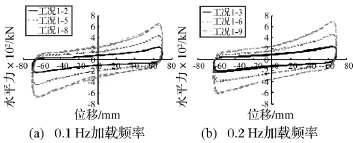
图9 相同频率、不同压力下滞回曲线对比Fig.9 Comparison of the hysteretic loops with varied vertical pressure

图9给出了相同加载频率、不同竖向压力下的滞回曲线的对比。图9表明，在相同加载频率下，随竖向压力的增大，支座的滞回耗能能力呈增大趋势，滞回曲线的水平力幅值的增长与竖向压力增幅相当。

(2)摩擦系数分析

摩擦系数分析采用表1各工况的测试结果，利用位移-时间曲线和水平力-时间曲线，推导出水平力-位移曲线，根据理论模型推算出摩擦系数。测试表明，支座在滑动过程中摩擦系数存在差异，表2给出了支座水平位移为0、+A/2和+A处的摩擦系数均值，其中A为支座水平最大位移。

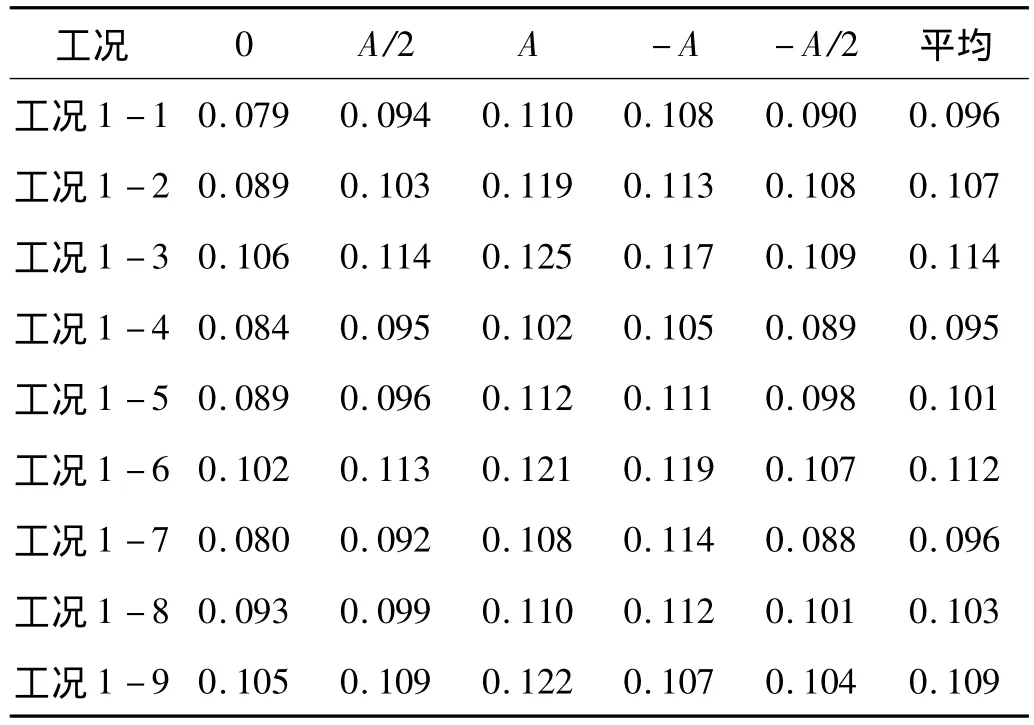
表2 各工况下支座摩擦系数Tab.2 Friction Coefficient Under Various Conditions

由表2可知，支座摩擦面间的摩擦系数平均值在0.096-0.109之间变化，表明采用新型摩擦材料制作的滑槽与滑块间的摩擦系数基本能满足要求。

为了分析竖向压力对摩擦系数的影响，图10给出了相同加载频率不同竖向压力下各工况的摩擦系数。

由图10可知，滑块在滑槽最低点即水平位移为0时摩擦系数最小，随着水平位移增大摩擦系数呈增大趋势。支座在相同加载频率不同压力作用下摩擦系数变化不大，没有明显变化规律，证明竖向压力对摩擦系数影响较小。

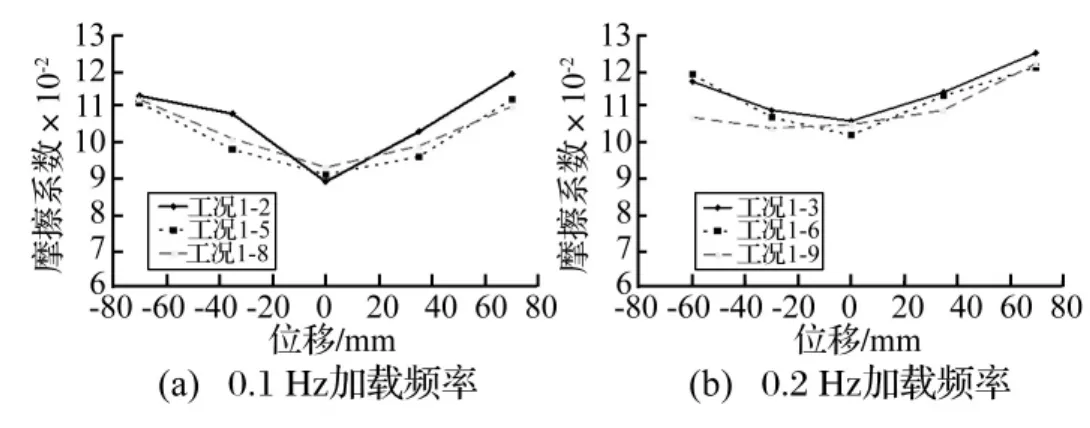
图10 相同加载频率不同压力下摩擦系数对比Fig.10 Comparison of friction coefficient with varied vertical pressure

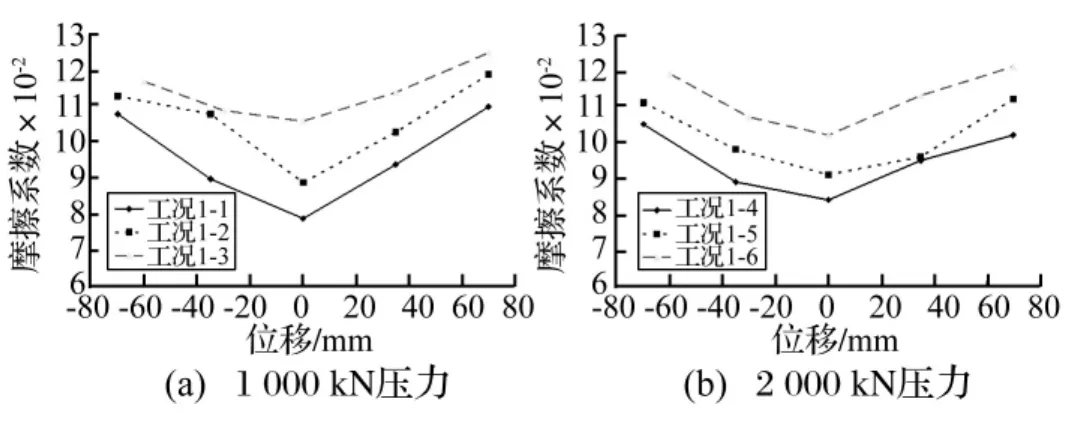
图11 相同压力不同加载频率下摩擦系数对比Fig.11 Comparison of friction coefficient with varied input frequencies

图11给出了将相同竖向压力、不同加载频率下各工况的摩擦系数对比曲线。由图11看出，滑块在滑槽最低点即水平位移为0时摩擦系数最小，随着水平位移增大摩擦系数呈增大趋势。在相同压力作用下，随着加载频率的增大，摩擦系数整体呈增大趋势，支座耗能能力增强，这与文献［7］中关于Teflon与不锈钢摩擦测试结果类似。

3 试验结果与理论模型对比分析

3.1 试验结果与数值模拟滞回曲线

数值模拟分析采用ABAQUS有限元软件，模拟采用的试验测定之表2中的摩擦系数，建模利用旋转实体快速生成。在本文分析中，未考虑支座板的螺栓洞口。在网格划分过程中，分析时均选用8节点六面体线性减缩积分单元(C3D8R)，该单元适合于弹塑性分析和接触分析。在采用C3D8R单元分析时，是通过结构化网格技术进行划分的，选用中性轴算法(Medial Axis)，该算法容易得到单元形状规则的网格［16-17］。由于支座各部分的构成不规整，较为复杂，不能直接采用结构或扫略网格划分，此时可先将该实体分割(Partition)为几个简单区域，然后再进行划分，网格划分如图12所示。在接触面定义、约束定义和加载定义等方面，根据不同的分析内容采用相应的定义方式。

在材料本构关系选择上，本章中模型采用弹塑性模型，钢材的弹性模量取E=2.1×105 MPa，泊松比υ=0.3，设计强度为210 N/mm2，塑性材料数据如表3所示。

表3 材料真实应力与塑性应变的关系Tab.3 Relationship between plastic deformation and real stress of the steel materials

图12 网格划分示意图Fig.12 Grids division of the FPS bearing

依据理论分析与试验结果，将支座在各工况下的理论滞回曲线、数值模拟滞回曲线和试验滞回曲线进行对比，图13给出了四类工况下滞回曲线对比，其中理论值是按式(1)计算的结果。

由图13可知，试验所得滞回曲线与理论模型和数值模拟结果吻合较好，可以验证理论力学模型的正确性和数值模拟结果的准确性。

然而，在整体吻合的情况下，试验所得滞回曲线与理论结果还是存在一定差异，主要表现在以下几方面:① 支座的水平刚度不断变化，在平衡位置水平刚度较小，在最大位移处水平刚度最大;② 支座由负向最大位移向正向最大位移运动时，试验测得耗能能力低于理论耗能能力;③ 水平位移在零点位置时，试验采集的水平力低于理论值，而在最大位移处，试验采集到的水平力与理论值相差不大。

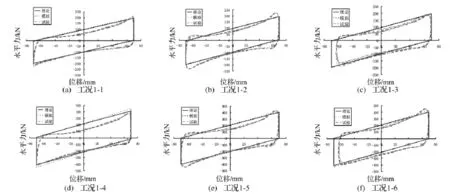
图13 理论滞回与试验滞回曲线对比Fig.13 Hysteretic loops comparison between theoretical and experimental

3.2 误差分析

试验结果和理论模型的对比分析可以看出本次试验结果较为理想，但试验所得支座滞回曲线与理论模型拟合值间还存在差异。差异产生的原因主要表现在以下几个方面:

(1)试验设备的系统误差

本次试验所使用的4 000 t多功能液压伺服加载设备的系统误差为加载量程的+1%;水平位移量程为+600 mm，误差为+6 mm，设备系统误差对于本次试验的影响偏大。试验过程中，为了避免这些误差，在竖向加载过程采用了输出荷载控制加载，即缓慢调整输入荷载同时关注输出荷载，当输出荷载稳定在所需加载数值时，开始进行试验。同时，在位移输入时，也未使用试验设备自身的位移控制系统，而是采用两个位移传感器进行位移控制和数据采集。这样，从很大程度上避免了设备的系统误差，但是设备的系统误差必然存在，也必然会对试验结果产生一定影响。

(2)数据采集误差

本次试验使用的是IMP359551B型静态数据采集系统，采集参数16位，采集频率1 Hz。由于数据采集是静态采集，采集频率较低，也可能造成试验数据采集误差。

(3)理论假设造成的误差

支座理论力学模型推导存在假设，如由于支座转角很小而忽略转角产生的影响;忽略了挡块和滑块之间的转动摩擦;用库伦模型简化滑动面间的摩擦系数而忽略了压力和滑动速度对摩擦系数的影响等。

(4)加工误差

由于加工能力所限，试验构件加工精度不能保证滑动面间的完全耦合，挡块和滑块球面间的关节也不能完全耦合，所以在试验中会产生相应误差。

4 结论

(1)在简谐激励作用下青铜基摩擦材料的摩擦摆支座具有良好的耗能能力，其滞回曲线为平行四边形，与传统的摩擦摆支座的滞回曲线具有相同的特征，呈刚塑性。因此，新开发的摩擦摆支座可考虑采用与Teflon摩擦摆支座的力学模型进行隔震结构的设计，为工程应用提供了方便。

(2)支座的性能试验表明，支座的水平隔震性能与竖向荷载、加载频率等因素相关。在相同压力不同加载频率下滞回性能变化不大，随着加载频率增大，最大位移处水平力略有增大，滞回曲线趋于饱满;在相同加载频率下，随竖向压力的增大，支座的滞回耗能能力呈增大趋势，其增幅比值与竖向压力增幅比值相当。

(3)支座滑动面间的摩擦系数平均值的变化范围在0.096-0.109之间。在相同压力作用下，随着加载频率的增大，摩擦系数整体呈增大趋势，支座耗能能力增强;而在相同加载频率不同压力作用下摩擦系数变化不大，没有明显变化规律，表明竖向压力对摩擦系数没有明显影响。

(4)结果表明试验所得滞回曲线与理论模型和数值模拟结果吻合较好，验证理论力学模型的合理性。

［1］ Zayas V，Low S，Mahin S.The FPS earthquake resisting system［R］. TechnicalReportUCB/EERC -87/01，University of California at Berkeley，1987.

［2］ Zayas V，Low S，Bozzo L.Feasibility and performance studies on improving the earthquake resistance of new and existing buildings using the friction pendulum system［R］.TechnicalReportUBC/EERC -89/09，University of California at Berkeley，1989.

［3］Zayas V，Piepenbrock T，Al-Hussaini T.Summary of testing of the friction pendulum seismic isolation system 1986-1993［C］.Preprint:Proc.，“ATC-17-1，Seminar on Seismic Isolation，Passive Energy Dissipation，and Active Control”，Applied Technology Council， Redwood City， CA94065，March，1993.

［4］Zayas V，Contantinou M C，Tsopelas P，et al.Testing of friction pendulum seismic isolation bearings for bridges［C］.The 4th World Congress On Joints And Bearings，Sacramento，California，1996.

［5］Constantinou M C，Caccese J，Harris H G.Frictional characteristics of teflon-steelinterfaces under dynamic conditions［J］. Earthquake Engineering and Structural Dynamics，1987，15(6):751-759.

［6］Mokha A S，Constantinou M C，Reinhorn A M.Teflon bearing in base isolation I:testing［J］.J.Structural Engineering，ASCE，1990，116(2):438-454.

［7］ Mokha A，Constantinou M，Reinhorn A.Experimental study of friction-pendulum isolation system［J］.J.Structural Engineering，ASCE，1991，117(4):1201-1217.

［8］Mokha A，Constantinou M，Reinhorn A.Verification of friction model of Teflon bearings under Triaxial load［J］ J.Structural Engineering，ASCE，1993，119(1):240-261.

［9］Roussis P，Constantinou M. Uplift-restraining friction pendulum seismic isolation system［J］.Earthquake Engineer Structure Dynamic，2006，35(5):577-593.

［10］ Roussis P，Constantinou M.Experimental and analytical studies of structures seismically isolated with an upliftrestraining friction pendulum system［J］.Earthquake Engineer Structure Dynamic，2006，35(5):595 611.

［11］ Constantinou M，Whittaker A S，Velivasakis E.Seismic evaluation and retrofit of the Ataturk international airport terminal building［C］.Research Progress and Accomplishment，MCEER Bulletin，2001.

［12］ Hitomi Y，Osawa K，Nakagawa M.Structural design of yamaguchi dome［C］.Proceedings of IASS 2001(Nagoya)，TP155，2001.

［13］ Kin Y C，Xue S D，Zhuang P，et al.Seismic isolation analysis of FPS bearings in spatial lattice shell structures［J］.Earthquake engineering and engineering vibration，2010，9(1):93-102.

［14］ AASHTO .Guide specifications for seismic isolation design［M］.Washington ，DC:AASHTO，1999.

［15］薛素铎，赵 伟，李雄彦.竖向抗拔型摩擦摆支座［P］.中国专利:CN101086152，2007-12-12.

［16］庄 茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用［M］.北京:清华大学出版社，2009.

［17］石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京:机械工业出版社，2006.