连通图含某些指定边生成树的环和矩阵生成法

孙文静, 胡茂林

(1.宁夏大学 数学计算机学院, 宁夏 银川 750021; 2.淮阴师范学院 数学科学学院, 江苏 淮安 223300)

连通图含某些指定边生成树的环和矩阵生成法

孙文静1,2, 胡茂林2

(1.宁夏大学 数学计算机学院, 宁夏 银川 750021; 2.淮阴师范学院 数学科学学院, 江苏 淮安 223300)

提出并研究了连通图含某些指定边的生成树的生成问题.在给出环补关联矩阵与环和矩阵等定义的基础上,给出并证明了连通图含某些指定边的生成树的生成方法(环和矩阵法).利用环和矩阵法寻求图的特殊的生成树的方法、步骤以及其准确性和快捷性也在文中进行了讨论.

指定边; 生成树; 环补关联集; 环补关联矩阵; 环和矩阵

0 引言

我们知道求连通图的全部生成树有很多方法,如Johson给出的基本割集多项式相乘展开法[1]、Mayeda给出的基本树变换法[2]、朱绍文给出的两类K-树递推公式法[3]、胡茂林给出的全部生成树的组合生成法[4]等.在图论的应用中,常需要找出一个连通图的所有生成树.例如,在电网络的拓扑分析中,需要找出网络中所有可能的互异生成树.但在实际中往往需要求出一个连通图的含某些指定边的生成树.例如,一个有n座城市组成的地区,城市1至n编号,为了地区经济的快速发展,决定其中一些城市可以修建高速铁路.由于某几个城市经济特别繁荣且考虑到建设成本,因此决定在这几个经济特别繁荣的城市间修建直达的高速铁路且这几城市间高铁不形成环.这就需要求出一个连通图的含某些指定边的生成树.因此,本文将在文[4]的基础上介绍连通图含某些指定边的生成树的一种方法(环和矩阵法).为此,我们给出含某些指定边的图顶点的相关关联集、环补关联集定义,在此基础上把含某些指定边环补关联集向量及自环补关联集向量的不重并组成矩阵,这样就可减少很多不必要的运算,从而准确快捷地得到指定的全部生成树.在本文中,若非特别声明,大写字母G一般表示一个图,G(p,q)一般表示一个具有p个顶点q条边的图.另外,还用到下面概念和运算.

关联集: 设v是图G的一个顶点,与v关联的所有边的集合,称为顶点v的关联集,记作S(v).

集合环和运算: 设A,B是两个集合,则称集合{x|x∈(AB)Y(BA)}为集合A与B的环和或对称差,记为A⨁B,并称符号⨁为集合的环和运算.

模2加法: 0+0=0,1+0=1,1+1=0.

1 几个基本概念

在本节我们定义本文要用到的几个基本概念即相关关联集、环补关联集、环补关联矩阵、参考环补关联矩阵和环和矩阵等.

定义2 设边a1,a2,…,ak(1≤k≤p-1)是具有p个顶点q条边的图G(p,q)的给定的k条边,如果G的一个关联集S(v)含指定边ai1,ai2,…,ail,其中{ai1,ai2,…,ail}⊂{a1,a2,…,ak},则称该关联集为图G(p,q)与指定边a1,a2,…,ak相关的关联集,记为Sai1ai2…ail(v),其中1≤l≤k.

定义3 对于图G(p,q)的指定边a1,a2,…,ak(1≤k≤p-1),若图G的几个关联集作环和运算所得的结果中含全部指定边a1,a2,…,ak,则称这几个关联集为图G的关于指定边a1,a2,…,ak的互为环补关联集.

特别地,若一个关联集本身含有指定边a1,a2,…,ak,则称这个关联集关于指定边a1,a2,…,ak还是自环补的.

定义4 一个图G(p,q)的关于指定边a1,a2,…,ak(1≤k≤p-1)的所有互为环补关联集的对应的关联向量以及所有自环补的关联集的对应的关联向量的不重并叫图G的关于指定边a1,a2,…,ak(1≤k≤p-1)的环补关联矩阵,记为M(G(a1,a2,…,ak));从M(G(a1,a2,…,ak))中任意删去一行所得到的矩阵叫图G的关于指定边a1,a2,…,ak的参考环补关联矩阵,记为M′(G(a1,a2,…,ak));删去的一行所对应的G的顶点叫参考点.

定理1 一图G(p,q)的任意两个关联集的环和等价于它们所对应的关联向量在{0,1}域上作模2加法.

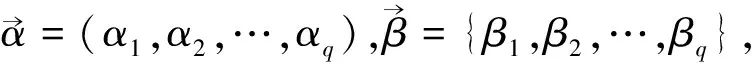
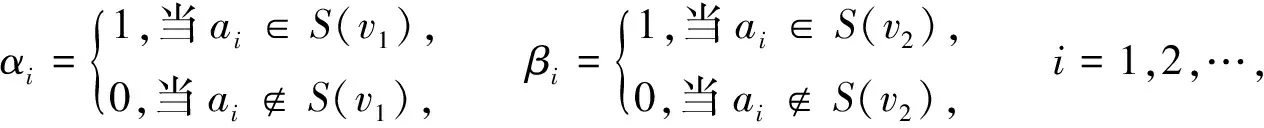
设S(v1)∩S(v2)={ajk,ajk+1,…,ajl},即aik=ajk,aik+1=ajk+1,…,ail=ajl,其中1≤k≤l≤min{m,n},

则

S(v1)⨁S(v2)={ai1,…,aik-1,ail+1,…,aim,aj1,…ajk-1,ajl+1,…ajn},

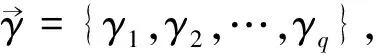
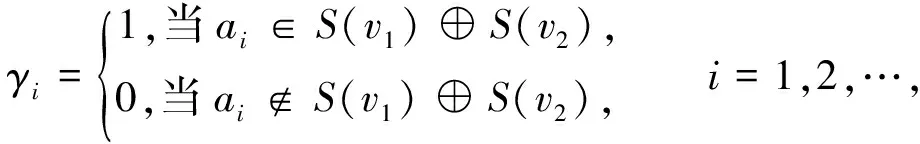
图1 一个(4,5)的连通标定图

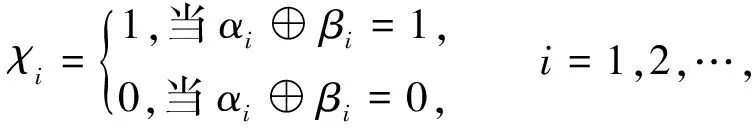
故

反之亦然.

定义5 对于图G(p,q)的指定边a1,a2,…,ak(1≤k≤p-1),把它的参考环补关联矩阵中各个自环补关联集以及各种互为环补的关联集作环和一起构成的矩阵叫图G关于指定边a1,a2,…,ak的环和矩阵,记作A.

例1 对图1所示的图G指定a,b边,求图G关于a,b的相关关联集、环补关联集、环补关联矩阵及环和矩阵.

图G的关联集为

S(1)={a,d,e};S(2)={a,b};S(3)={b,c,e};S(4)={c,d}.

因为图G指定边为a,b,所以图G关于a,b的相关关联集为

Sa(1)={a,d,e};Sa,b(2)={a,b};Sb(3)={b,c,e}.

又因为

Sa(1)⨁Sb(3)={a,b,c,d};Sa,b(2)⨁⟩={a,b};Sa(1)⨁Sb(3)⨁S(4)={a,b}.

所以图G关于指定边a,b的环补关联集为

Sa(1)与Sb(3);Sa(1),Sb(3)与S(4).

自环补关联集为

Sa,b(2)={a,b}.

因此图G关于指定边a,b的环补关联矩阵为

从M(G(a,b))中删去第四行即参考点为顶点4得到图G关于指定边a,b的参考环补关联矩阵为

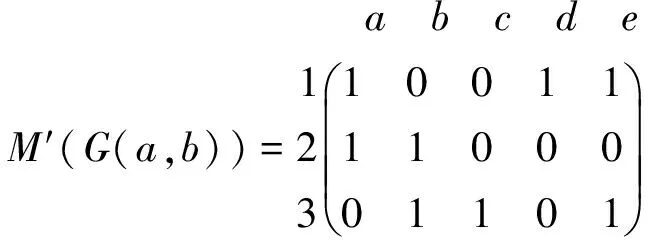
于是,图G关于指定边a,b的环和矩阵为

2 连通图含某些指定边的生成树的生成

引理1[4]设G是具有q条边的a1,a2,…,aq的p阶连通图,其增广关联矩阵是C,则由G的p-1条边aj1,aj2,…,ajp-1导出的G的子图T=aj1aj2…ajP-1是G的一棵生成树的充要条件是在C中存在唯一的一行,使得这行在第j1,j2,…,jp-1列处的元素都是1.

定理2 设G(p,q)具有q条边a1,a2,…,aq的p阶连通图,aj1,aj2,…,ajk(1≤k≤p-1)是G的k条指定边且由这k条边导出的G的子图不含圈,又设关于这k条边的一个环和矩阵为A,则T=ai1ai2…aip-1是G的一棵含指定边aj1,aj2,…,ajk生成树的充要条件是在A中存在唯一一行,使得这行在第i1,i2,…,ip-1列处元素都是1,其中有k个1元素在指定边所对应列上.

证明设图G的增广关联矩阵C是与G的环和矩阵A具有相同的参考点的G的一个增广关联矩阵.由于图G的环和矩阵A是它的增广关联矩阵C的所有行向量集合的一个子集组成的矩阵,因此矩阵A是与C同列且具有相同的参考点的C的子矩阵.

下面证明C在第j1,j2,…,jk列的所有元素都为1的每个行向量都在A中.

设α是C的在第j1,j2,…,jk位置元素都为1的行向量,令这个行向量对应的边集合为S,则S含有所有指定边,这样S有且仅有以下两种情况:

若S是G的一个自环补的关联集,由定义5则它对应的关联向量就在A中;

若S是G的几个关于指定边互为环补的关联集的环和,由定义5则它所对应的关联向量在A中.

必要性: 设T=ai1ai2…aip-1是G的一棵含指定边aj1,aj2,…,ajk的生成树,则由引理1[4]知,在矩阵C中存在唯一一行使得这行在第i1,i2,…,ip-1列的元素都为1.特别地在第j1,j2,…,jk列的元素都为1,因此这样的行向量必在A中.又由于A是C的子矩阵,故这个行向量在A中是唯一的.

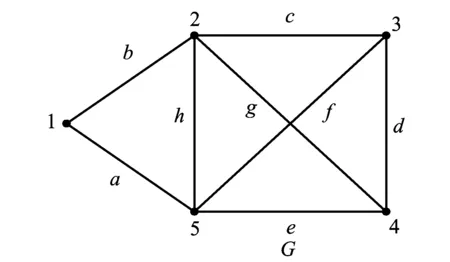
图2 一个(5,8)的连通标定图

充分性: 设α是A中唯一一行在第i1,i2,…,ip-1列的元素都为1且其中有k个1在指定边aj1,aj2,…,ajk所对应列上,则α同时也在C中.由引理[4]知T=ai1ai2…aip-1是G的一棵生成树.由于C中这样的α在第j1,j2,…,jk列的元素都为1,所以T含有指定边aj1,aj2,…,ajk,即T是含有指定边aj1,aj2,…,ajk的G的一棵生成树.

例2 对图2所示的图G指定a,b边,求图G含指定边a,b生成树.

图G的关联集为

S(1)={a,b};S(2)={b,c,g,h};S(3)={c,d,f};S(4)={d,e,g};S(5)={a,e,f,h}.

图G对于指定边a,b的相关关联集为

Sa,b(1)={a,b};Sb(2)={b,c,g,h};Sa(5)={a,e,f,h}.

因为

Sa,b(1)⨁φ={a,b};Sb(2)⨁Sa(5)={a,b,c,e,f,g};

Sb(2)⨁S(3)⨁Sa(5)={a,b,d,e,g};

Sb(2)⨁S(4)⨁Sa(5)={a,b,c,d,f};Sb(2)⨁S(3)⨁S(4)⨁Sa(5)={a,b}.

所以图G对于指定边a,b的环补关联集为

S(2)与S(5);S(2)、S(3)与S(5);S(2)、S(4)与S(5);S(2)、S(3)、S(4)与S(5).

自环补关联集为

Sa,b(1)={a,b}.

图G对于指定边a,b的环补关联矩阵为

从M(G(a,b))中删去第五行即选参考点为顶点5得图G对于指定边a,b的参考环补关联矩阵为

图G对于指定边a,b的环和矩阵为

由定理2可知图G中含指定边a,b生成树有

abcd,abdf;abde,abdg;abce,abcg,abef,abfg.

[1] Johson D E, Johonson J R. Graph Theory with Engineering Application[M]. NewYork: Ronald Press,1972.

[2] Mayeda W. Graph Theory[M]. NewYork: Wiley-Intrsience, 1972.

[3] 朱绍文, 陈洪陶. 全部生成树的一种生成方法[J]. 兰州大学学报:自然科学版,1988,24(4):64-70.

[4] 胡茂林, 蔺勇. 全部生成树的组合生成法[J]. 陕西科技大学学报,2004,22(1):124-126.

TheRingSumMatrixGeneratingMethodofSpanningTreesContainingCertainAppointedEdgesinConnectedGraph

SUN Wen-jing1,2, HU Mao-lin2

(1.School of Mathematics and Computer Science, Ningxia University, Yinchuan Ningxia 750001, China)(2.School of Mathematical Science, Huaiyin Normal University, Huaian Jiangsu 223300, China)

In this paper, the generating problem of the spanning tree containing some prescribed edges is posed and discussed. This paper gives and proves the generating method after defining the related definitions and notations of the ring complement in-cidence matrix and ring sum matrix. The method, step and the accuracy, immediacy of the method seeking the particular spanning tree using the ring sum matrix method is also further discussed

prescribed edges; spanning trees; ring complement incidence set; ring complement incidence matrix; ring sum matrix

2013-04-05

孙文静(1985-), 女, 江苏宿迁人, 硕士研究生, 研究方向为图论.

O157.5

A

1671-6876(2013)03-0208-05

[责任编辑李春红]