MATLAB在支路电流法教学中的应用
侯 丽,刘 琦
(黄山学院 机电与信息工程学院,安徽 黄山245041)
1 引 言
支路电流法是以支路电流为电路未知量列写电路方程分析电路的方法。列写的是独立的KCL 和KVL 方程。[1]方程列写方便、直观,但因方程数较多,求解比较繁琐。因而急需找到一种快速的、简捷的求解方法。MATLAB 是一套高性能的数值计算和可视化软件,具有强大的矩阵处理功能,极大地方便了科学计算和工程问题的求解。[2]
因此,利用MATLAB 强大的矩阵计算功能进行支路电流法的求解,使得课堂教学中更专注于电路问题的分析和讨论,能够改善课堂教学效果。
2 支路电流法的一般步骤
对于有n 个结点、b 条支路的电路,要求解各支路电流,未知量共有b 个,只要列出b 个独立的电路方程,便可以求解出b 个支路电流未知量。具体步骤如下:
1.标定各支路电流的参考方向;
2.从n 个结点中任意选择n-1 个结点,列写KCL 方程;
3.选择b-(n-1)个基本回路,指定回路绕行方向,列写KVL 方程;
4.求解上述方程,得到b 个支路电流;
5.进一步计算支路电压和进行其他分析。
3 支路电流法的难点
当电路中含有理想电流源和受控源时,如何列写支路电流方程,是支路电流法的难点。
当电路中含理想电流源支路时,可采用避开电流源支路取回路的方法。因为理想电流源所在支路的电流为已知量,电路中含有多少条理想电流源支路,相当于减少了对应数目的支路电流未知量,减少了对应数目的KVL 方程数。
当电路中含有受控源时,方程的列写分两步:首先将受控源看作独立源列方程;然后将控制量用未知量表示,并代入所列的方程,消去中间变量。
4 MATLAB 在支路电流法中的应用
利用MATLAB 强大的矩阵计算功能求解手工建立的支路电流方程。现以图1 电路模型为例,说明MATLAB 求解过程。
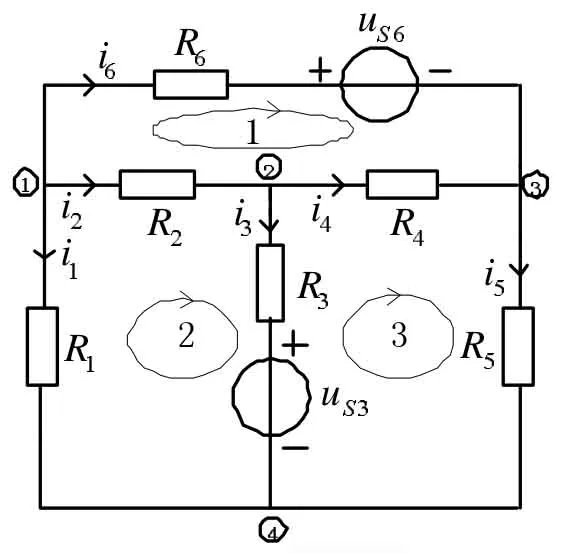
图1
其参数设置如下:
R1=R2=10Ω,R3=4Ω,R4=R5=8Ω,R6=2Ω,uS3=20V,uS6=40V,
图1 中共有i1-i6个支路电流未知量,需列写6个独立的方程,按照图示的电流参考方向和回路绕行方向,列方程如下:
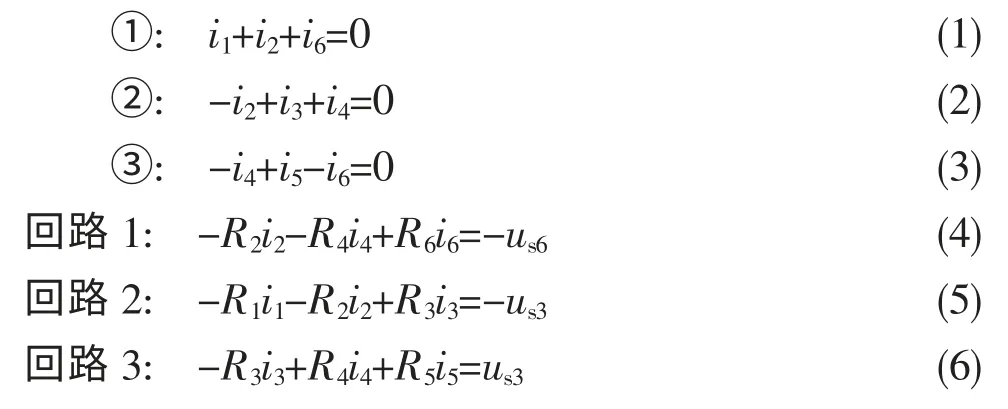
将式(1)-(6)写成矩阵形式:
AX=B
式中:
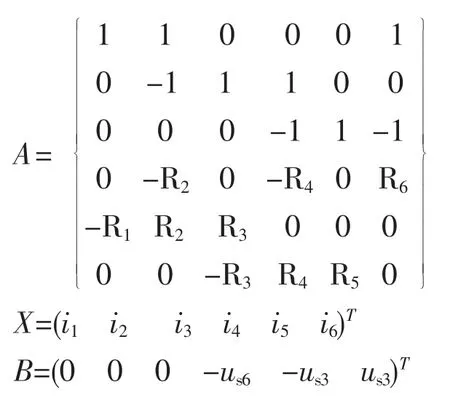
其中A为系数矩阵,取决于电路元件的参数,X是由支路电流未知量构成的列向量。B是与电压源的电压有关的列向量。
在MATLAB 命令菜单中输入edit 命令进入程序编辑器,编辑文件。运行下述程序:
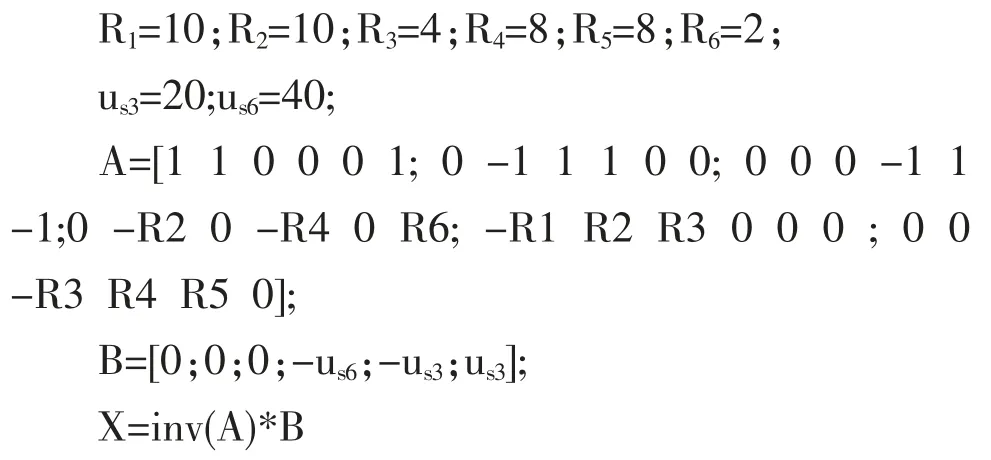
得到以下运行结果:

5 结 论
本文利用MATLAB 软件强大的矩阵计算功能进行支路电流法的求解,相比手工求解,极大地减少了课堂教学中进行电路运算的时间,使得课堂教学中能把精力更集中于电路问题的分析和讨论中,明显改善了课堂教学效果,并提高了学生分析问题和解决问题的能力。因此利用MATLAB 软件进行电路问题的求解,在电路分析课程教学中具有很好的应用价值。
[1]邱关源.电 路(第5 版)[M].北京:高 等教育出版 社,2006:58-60.
[2]李海涛.MATLAB 程序设计[M].北京:高等教育出版社,2005:28-30.

