主成分分析法在生物科学专业学生成绩评价中的应用

陈向阳

（黄山学院 生命与环境科学学院，安徽 黄山245041）

1 引 言

学生学习成绩是衡量学生学习情况的重要指标，是教师教学效果的重要反映。[1]如何准确、客观、全面、科学地评价学生的学业综合成绩对学生和教师都是非常重要的。目前大部分高校主要采用总平均学分绩点或平均分作为评价学生综合成绩的手段，但方法能否全面反映学生的综合成绩，这个问题一直让许多高校和学者产生疑问，本文采用主成分分析法来对学生成绩进行科学的评价和学科间具体的优势、劣势的度量。[2]

2 主成分分析法

2.1 主成分分析法

主成分分析是把多个指标化为少数几个综合指标的一种统计方法，去解释原来资料中的大部分变异。在实际问题研究中，为了全面、系统地分析问题，往往要考虑众多影响因素，这些涉及的因素一般称为指标或者变量。因为每个变量都在不同程度上反映了所研究问题的某些信息，并且变量之间彼此也存在一定的相关性，即所得的统计数据反映的信息在一定程度上会有重叠。因此，人们会很自然地想到，能否在相关分析的基础上，用较少的新变量代替原来较多的变量，而且使这些较少的新变量尽可能多地保留原来变量所反映的信息？主成分分析法就能解决这一问题，即在众多的因素中不损失或很少损失原有信息的基础上，将原始的多个彼此存在相关性的变量转化为少数几个彼此不相关或彼此独立的，能综合评价学生成绩的一种多因素方法。从数学角度来看，这是一种降维处理技术。[3]

2.2 主成分分析法的步骤

1.建立观测数据矩阵。设有n 个样本，每个样本有m 个指标：x1，x2，…，xm，将所有样本写成矩阵形式记为X=(xij)n×m

2.对原始数据进行标准化处理，得

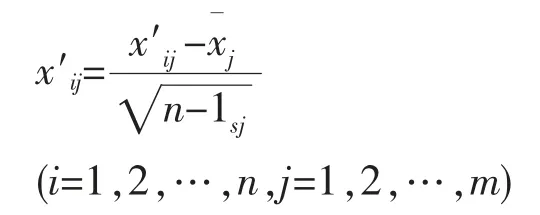
式中xij——原始数据；

x′ij——标准化后的数据；

n—样本容量；

m—指标变量数。标准化后的数据矩阵仍然记为X=(xij)n×m。

3.计算相关系数矩阵R=(rij)n×m的特征值λ 与对应的特征向量αj(j=1,2,…,m)。

4.计算主成分载荷lij，即主成分中xi的系数lij=。

5.依据特征值和累积贡献率确定所需主成分的个数p，使p 满足：

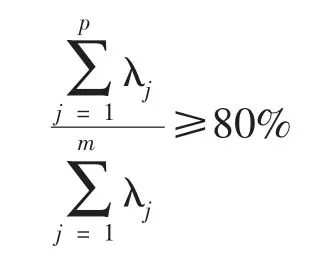
6.计算得出主成分分值，解释主成分含义，对影响学生公共必修课和专业必修课成绩的诸多因素进行分析和评价。[4]

3 结果与分析

以黄山学院生命与环境科学学院生物科学专业09 级学生在大一-大三的3 学年的考试课成绩为例，运用主成分分析法对学生的综合学习效果和综合能力进行评价。该班总共有78 名学生，随机抽取25 名同学的考试科目成绩作为样本，即研究对象。该专业3年总共开设了30 多门课程，经过生物科学专业视角的初步遴选，确定以15 门主干课程成绩作为指标（或称变量），所选课程为B1（大学体育）、B2（大学物理）、B3（C 语言程序设计）、B4（马克思主义基本原理概论）、B5（大学英语）、B6（高等数学）、B7（有机化学）、B8（动物学）、B9（植物学）、B10（生物化学）、B11（微生物学）、B12（细胞生物学）、B13（遗传学）、B14（植物生理学）、B15（分子生物学），其中B1-B6为公共必修课，B7-B15为专业必修课，以上15 门课程对应的成绩用x1、x2、x3、x4、x5、x6、x7、x8、x9、x10、x11、x12、x13、x14、x15来表示，这样即可得到一个25×15 的数据矩阵，使用DPS 进行主成分分析可得到相关系数矩阵、特征值及贡献率表以及主成分的特征向量与相应的载荷值表，见表1-表3。

由表1 可以看出，在被进行统计的15 门课程中，有14 门课程成绩间的相关系数为正值，即正相关，只有大学体育与多门课程之间的相关系数为负值，即负相关，并且多数课程之间的相关系数都达到了显著或极显著，这表示多数课程成绩间具有较强的可比性，即某门课程的成绩高低，可由另外一门课程成绩的高低分布规律大致推断。以有机化学（B7）和分子生物学（B15）为例，二者之间的相关系数最高（0.827），这表明有机化学掌握较好的同学，其分子生物学掌握的也较好。此外，对于生物科学专业开设的公共必修课和专业必修课对大学物理（B2）的依赖性较重，而高等数学（B6）和有机化学（B7）与绝大多数课程的相关系数都在0.4 以上，这充分地说明了在大学一年级时学好这两门课对生物科学专业本科生具有重要的影响。动物学（B8）、植物学（B9）和生物化学（B10）与所有的专业必修课之间的相关系数都在0.4 以上，达到了显著相关，这3 门课程也是生物类专业重要的专业基础课，这有力地验证了学好这3 门课程对专业知识的掌握至关重要。大学体育（B1）与多数课程的相关系数较小，甚至与多数课程出现了负相关，这可能是课程性质的缘故，这就要求教师合理引导学生转变思维方式，尤其是班级辅导员要在这方面进行充分分析，更加重视大学体育。

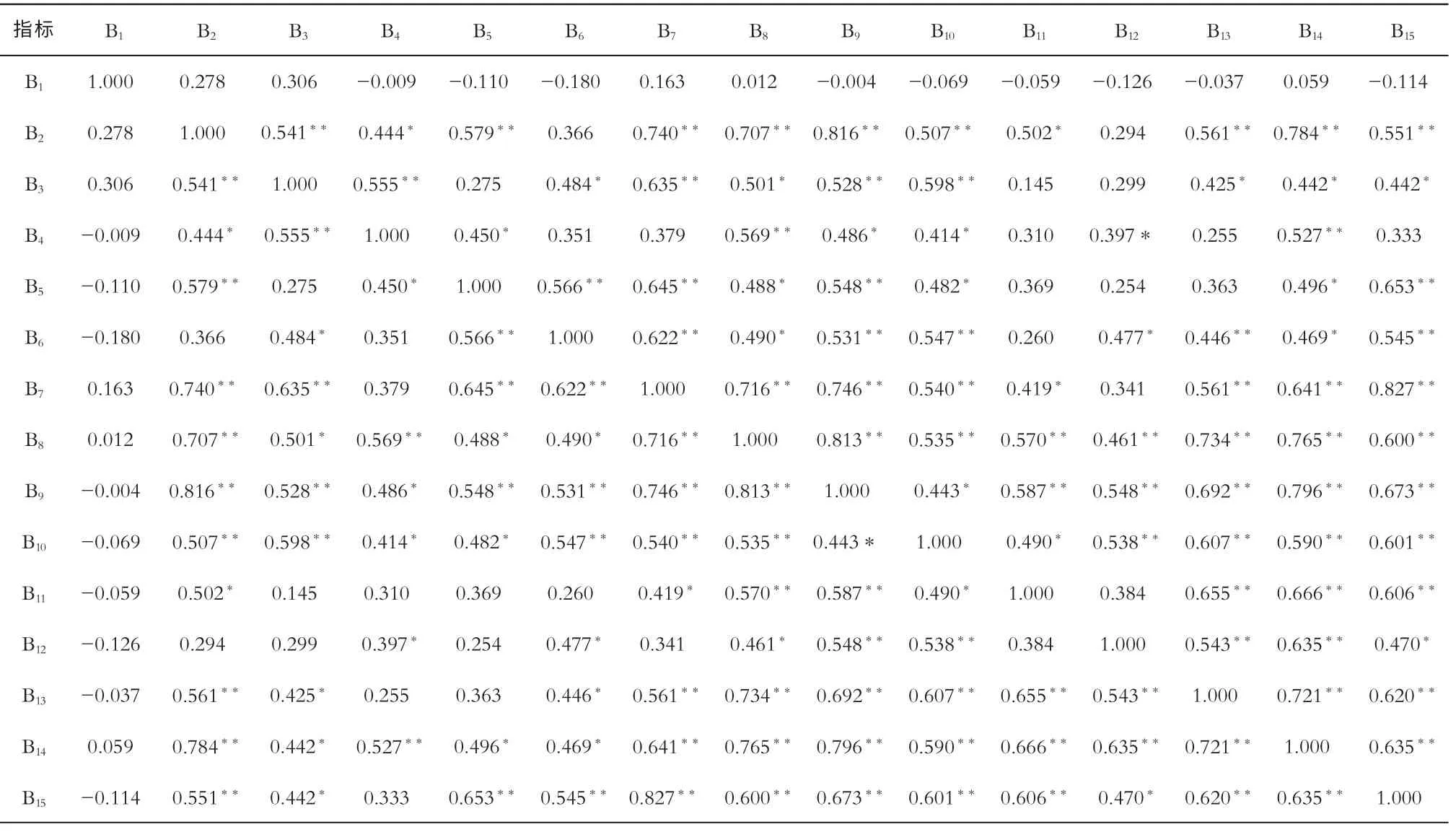
表1 公共必修课指标间相关系数

由表2 可以看出，前第一主成分的方差贡献率高达53.410%，即第一主成分可以反映原指标53.410%的信息量，表示第一主成分承载了学生成绩的主要综合信息。前5 个主成分的累积方差贡献率以高达82.935%，若按照80%的判断标准，只需选取前5 个主成分就可以代表原来15 个指标所包含信息量的82.935%。

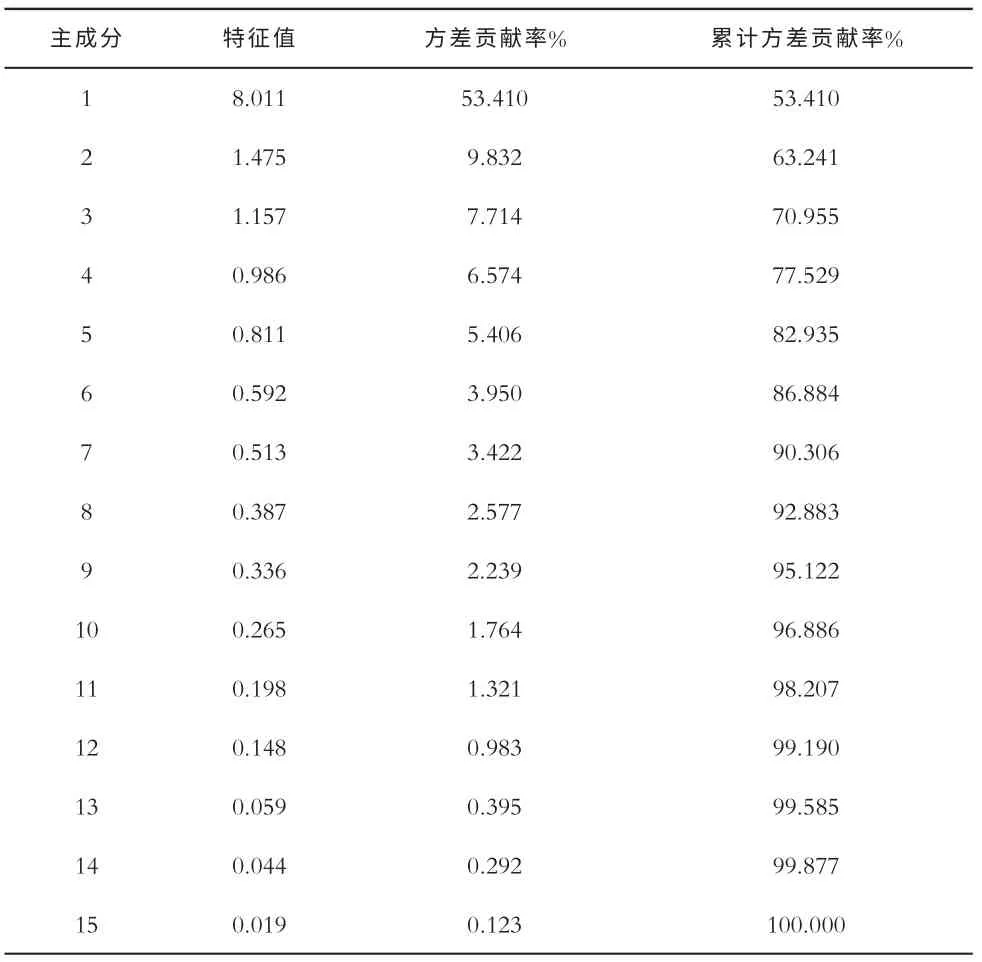
表2 主成分的特征值、方差贡献率和累计贡献率

表3 给出了前5 个主成分的特征向量和相应的载荷值。第一主成分对应的特征向量和载荷值均为正值，数值上也相差较小，即第一主成分可以反映学生的综合学习成绩。第一主成分在有机化学、动物学、植物学和植物生理学专业基础课程上的载荷值较大，可以认为这4 门课程在第一主成分中起作用较大，因此在大一和大二这几门课学得怎样就直接影响学生的综合专业素质。第二主成分的方差贡献率只有9.832%，且在各门课程上的载荷值有正有负，在评价学生综合成绩容易对结果产生偏差，剩下的3 个主成分与第二主成分的情况类似，因此直接可以利用第一主成分对学生综合成绩进行合理的评价。依据表3 可以计算25 名学生的选定数量主成分上的得分。

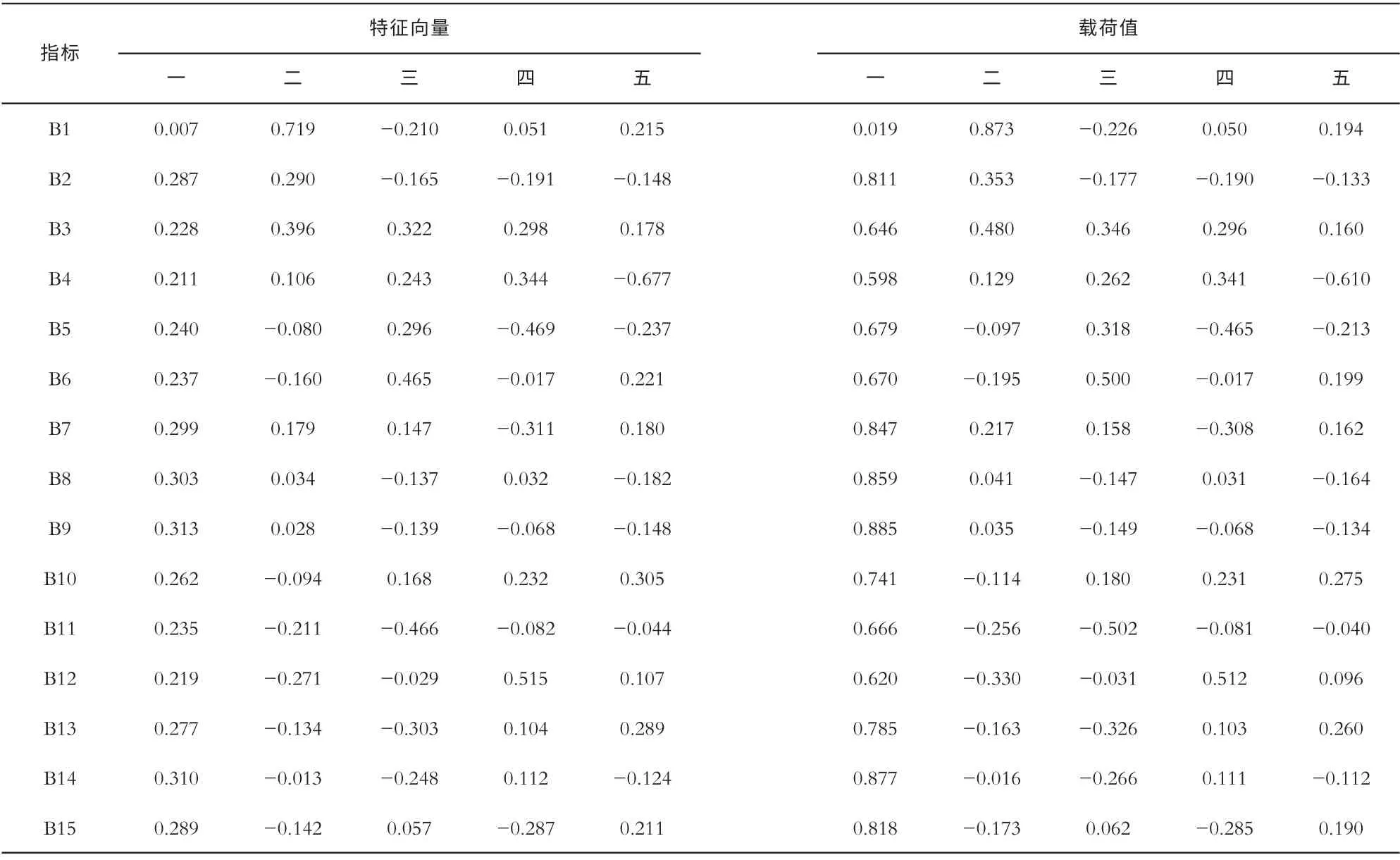
表3 5 个主成分的特征向量和相应的载荷值

第一主成分：

y1=0.007x1+0.287x2+0.228x3+0.211xx4+0.240x5+0.237x6+0.299x7+0.303x8+0.313x9+0.262x10+0.235x11+0.219x12+0.277x13+0.310x14+0.289x15

以此类推，通过表3 还可以写出其余4 个主成分的得分表达式。对于学习综合成绩的优劣也可以通过综合评价得分体现，其表达式为：

Y=8.011y1+1.475y2+1.157y3+0.986y4+0.811y5

将学生成绩标准化后的数据代入y1、y2、y3、y4、y5和Y的表达式中，就可以得到每位同学的主成分得分、综合得分，进而对25 同学3年来的学习效果进行综合排序（表4）。从表4 可以看出，第一主成分得分给出的排名与5 个主成分的综合得分提供的排名十分接近，平均分排名与主成分得分排名差距较大。从表4 中每名同学的综合成绩得分、总成绩平均分以及在5 个主成分方面的得分情况，可以进一步判断学生在综合素质和学科上的优劣。

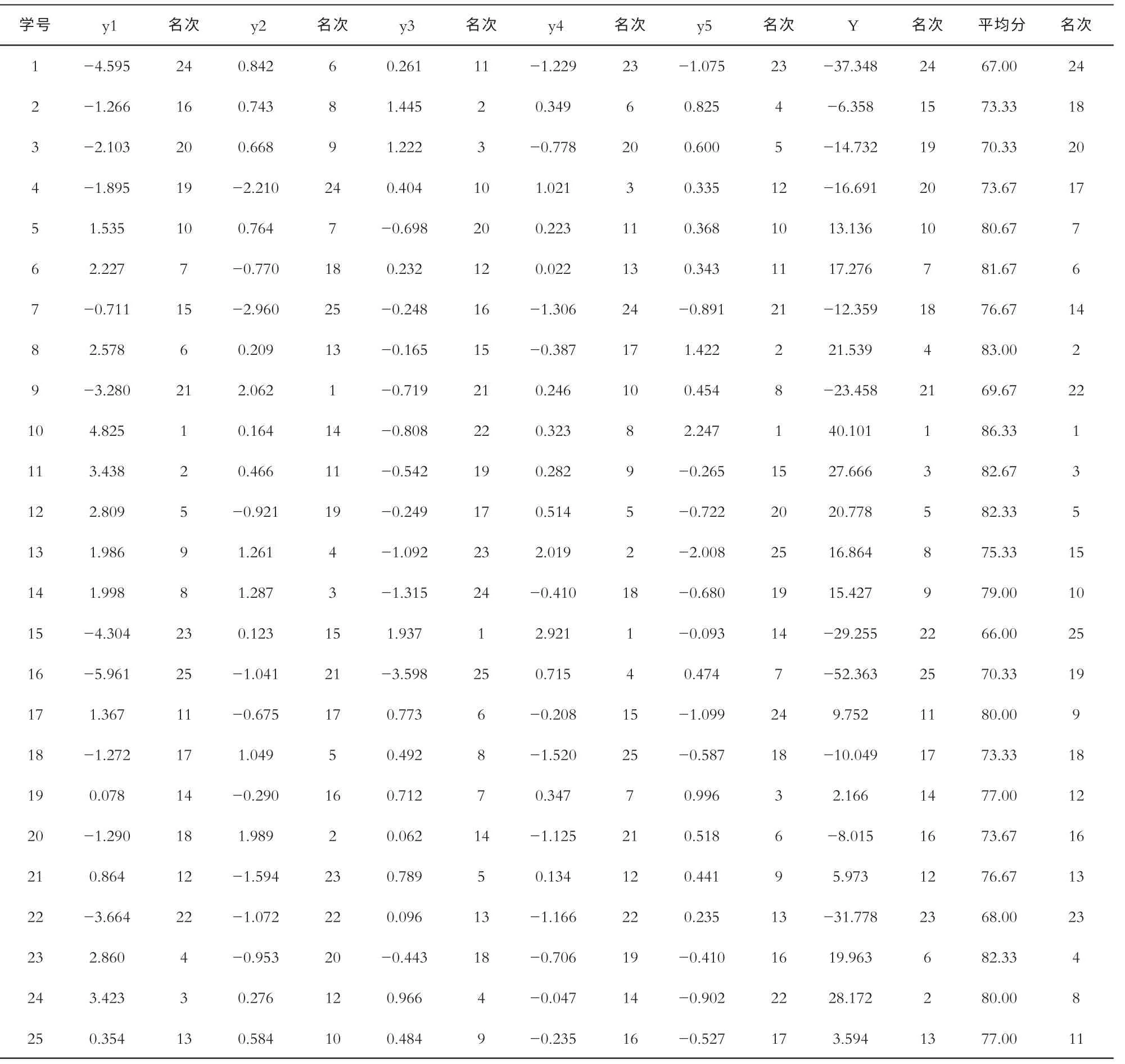
表4 综合排序

4 结 论

学生成绩可以反映学生的学习能力和综合素质，但是通过15 门课程来评价学生的学习能力又是一个复杂的问题，本文采用主成分分析的思想与实际教学情况相结合，从枯燥的各科目成绩中挖掘出很多信息，如各门课程成绩之间具有较强的相关性，学好后续专业必修课对动物学、植物学和生物化学等科目的依赖性，高等数学作为公共必修课对专业课学习的基础性作用，如何从主成分得分情况客观综合评价每位学生，体育课与理论课的关系该如何处理，等。

本文只是选择公共必修课和专业必修课进行统计分析，没有考虑公共选修课、专业限选课对学生学习成绩的影响，可能在分析综合成绩方面存在偏差。但是通过以上的数据分析，还是能发现教学的一些规律，旨在为生物科学专业教育教学改革提供科学的方法和理论依据。

[1]宫一博，魏军．多元统计分析在体育成绩评价中的应用[J]．吉林师范大学学报，2011，（2）：149-151．

[2]陈忠维，惠淑荣，董建国．主成分分析法在专业基础课成绩分析中的应用[J]．高等农业教育，2011，（6）：42-44．

[3]唐启义．实用统计分析及其DPS 数据处理系统[M]．北京：科学出版社，2009：761-771．

[4]罗双华，王芬玲．多元统计在研究专业课成绩影响因素中的应用[J]．桂林电子工业学院学报，2005,25，（2）：41-44．