旋转对称布尔函数线性结构的2个公开问题

赵亚群，李旭

（1. 信息工程大学 四院，河南 郑州 450002；2. 信息工程大学 数学工程与先进计算国家重点实验室，河南 郑州 450002）

1 引言

旋转对称布尔函数(RSBF, rotation symmetric boolean function)是一类具有特殊代数结构的布尔函数，由Pieprzyk和Qu[1]最先提出并应用于散列算法中。由于其良好的结构特性和在散列算法中广泛的应用，RSBF受到了极大的关注，RSBF的密码学性质一直是研究的热点问题[2~6]。其中，线性结构是度量布尔函数安全性的一个重要指标，具有非零线性结构的布尔函数是密码学中的一类“弱函数”。因此，研究RSBF的线性结构对于密码算法的安全性设计是很有意义的。

Elsheh在文献[7]中系统地研究了RSBF的线性结构，证明了 1n- 次RSBF不存在除全0和全1的线性结构，并提出了2个公开问题：对任意的 3n＞ ，n-1次偶变元平衡 RSBF和 n - 2次奇变元 RSBF均不存在非零线性结构。当 n ≤ 1 0时，Elsheh通过计算机验证了这2个公开问题的正确性。在此基础上，本文进一步研究了RSBF的线性结构，完全证明了公开问题1，给出了公开问题2成立的充分条件以及不成立的必要条件。

2 预备知识

12n1x2,… ,xn)∈F2。记Bn为所有n变元布尔函数构成的集合。

任意一个 Bn中的布尔函数 f ( x)都可以唯一地表示成 F2上的多变元多项式。

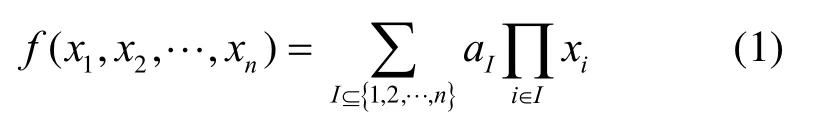
其中，aI∈F2，式(1)称为f( x)的代数正规型（ANF,algebraic normal form）。定义布尔函数 f ( x)的代数次数deg f为ANF中系数非零次数最高的单项式次数。若deg f≤ 1，则称 f ( x)为仿射函数，An表示 Bn中的全体仿射函数。定义 f( x)∈ Bn的支撑集，那么 f ( x)的汉明重量表示集合M的元素个数)。若wt( f) = 2n-1，则称 f ( x)为平衡函数。对任意的x = (x1, x2, … , xn)∈，定义x的支撑集为 W S( x)=那么x的汉明重量 w t( x)=对任意的 I ⊆ ｛ 1, 2, … ,n ｝ ，有

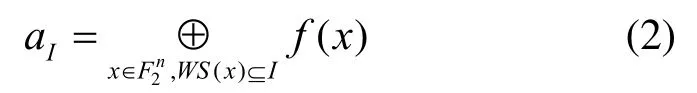
关于弹性(相关免疫)函数的谱特征有如下定义。

引理1[8]设 f ( x)∈ Bn，f( x)具有m阶弹性(相关免疫性)，当且仅当对任意的 w ∈Fn且

20 ≤ w t( w) ≤ m (1 ≤ w t( w) ≤ m )时，有 S(f)(w) = 0 。

定义 2 设 f ( x)∈ Bn，s∈，记Δsf( x)=f( x) ⊕ f ( x ⊕ s )。若对所有的 x ∈，都有Δf( x)=

sΔsf ( 0)=常数(0或1)，则称s为 f ( x)的一个线性结构。

定义 3 设 n为正整数，对任意的 x = (x1,和0≤k≤n -1，定义，其中，

3 2个关于RSBF线性结构的公开问题

首先，给出文献[7]中关于RSBF的一些基本性质。

引理2 设 f ( x)∈ Bn为RSBF，则有如下描述。

1) 若 α ∈F2n为f( x)的一个线性结构，那么对任意的 β ∈Gn( α)， β 仍为f( x)的线性结构。

2) 若deg f = n ，那么 f ( x)不存在非零线性结构。

3) 若deg f = n - 1 ，那么 f ( x)不存在除0和1以外的线性结构。

在文献[7]的最后，Elsheh通过对n元RSBF的考察，提出了2个关于RSBF线性结构的公开问题：对任意的 n ＞ 3 ，1) 代数次数为 n -1的偶变元平衡RSBF不存在非零线性结构；2) 代数次数为 n - 2的奇变元RSBF不存在非零线性结构。

注：由于任意向量均为线性布尔函数的线性结构，因此，在讨论布尔函数的线性结构时，所涉及的布尔函数均默认为非线性布尔函数。故文献[7]提出的2个公开问题中，有 n ＞ 3 的条件。

首先，给出公开问题1的证明。

引理 3[9]设，那么(i=0或 1)的充分必要条件是对任意的 w ∈且ws= i⊕ 1，都有 S（f）（w）= 0 。

引理4[9]设 f ( x)∈ Bn具有m阶相关免疫性，degf = k ，则k + m ≤ n 。若设 f （ x） 是平衡的，且1≤m ≤ n -2，则 k +m≤n-1。

定理1 设 f ( x)∈ Bn为RSBF(n为偶数且n＞3)，若deg f = n -1， w t( f) = 2n-1，那么 f ( x)不存在非零线性结构。

证明 根据引理 2中的 3)，只需证明 1不是f( x)的线性结构。

在讨论公开问题2之前，先引入FP(fast point)的概念及其部分性质。

定义4[10]设＜ d eg f-1，则称c为 f ( x)的一个FP。

可见，非线性布尔函数 f ( x)的任一线性结构均为 f ( x)的一个FP。若c=0，则称c为 f ( x)的平凡FP；否则，称c为 f ( x)的非平凡FP。 f ( x)的全体FP构成上的一个线性子空间，也就是说，若的2个FP，那么α⊕β仍为f( x)的FP。

引理5[10]设 f ( x)∈ Bn(n≥3)，f( x)的ANF中只含有代数次数为 n - 2 的单项式，记其单项式的系数为存在Bn且 只含有n-2次 项}。对任意的f( x)∈F，f( x)有且只有3个非平凡FP，且其中任意的2个非平凡满足：

注：下文中出现的 ri,j均表示 n - 2 次单项式的系数。

定理 2 设 f ( x)∈ Bn，degf=k(k＞1)，令f( x) = g( x) ⊕ h ( x)，其中， g ( x)为 f ( x)中所有代数次数为k的单项式之和，那么 f ( x)的任意非零线性结构均为 g （ x）的非平凡FP。

证明 deg f = d egg = k ，deg h ≤k-1。易知，对任意的，有

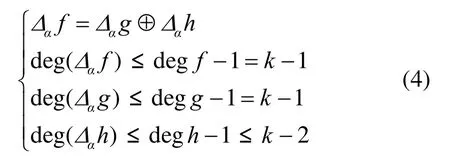
设 f(x) ∈ Bn为RSBF，degf = n - 2 ，令f( x) = g( x) ⊕ h ( x)，其中， g ( x)为 f ( x)中所有代数次数为 n-2的单项式之和，那么 g ( x)和 h( x)均为RSBF，且deg g = n - 2 ，deg h ≤n-3。

注：下文中出现的 g ( x)、 h ( x)和 f ( x)均具有如上关系。

定理 3 设 f ( x) ∈ Bn为RSBF(n为奇数且n＞ 3 )，若deg f = n - 2 ，那么：

证明 首先，证明 1不是 f ( x)的线性结构。g（ x）为只含有代数次数为 n - 2 的单项式的RSBF，不妨设 n - 2 次项出现，又 n为奇数，那么 n - 2 次项j≤n-1)均出现，即r1+j,i+j=1 (0≤j≤n-1)。

注：在不引起混淆的情况下，若i + j ＞ n ，笔者仍然用i+ j表示（i+ j） modn。

假设1是 f ( x)的线性结构，由定理2可知，1是 g ( x)的一个非平凡FP。由引理5可知 g ( x)存在其他2个非平凡FP，设其中的一个为 c ∈F2n，根据式(3)有

2f( x)不存在非零线性结构。

n 1,1)k)={(0,1,1)k,(1,0,1)k,(1,1,0)k}。事实上，笔者知道，那么 α ∈Gn((0,0,1)k)或Gn((0,1,1)k)。若 α ∈Gn((0,0,1)k)={(0,0,1)k,(0,1,0)k, (1,0,0)k}，有(0,0,1)k⊕ ( 0,1,0)k⊕ ( 1,0,0)k=1仍为 g ( x)的非平凡FP矛盾。可知， α ∈Gn((1,0,0)k)不是f( x)的线性结构。

若 α ∈Gn((0,1,1)k)为f( x)的线性结构，那么Gn((0,1,1)k)为 g ( x)的非平凡 FP。根据式(3)可得：f( x)中代数次数为 n - 2 的单项式的系数满足下式

4 结束语

本文利用了FP的一些性质，讨论了文献[7]提出的2个关于RSBF线性结构的2个公开问题。非线性布尔函数的线性结构必定为其FP，但布尔函数的非平凡 FP不一定是其非零线性结构。讨论线性结构和FP之间的关系以及对公开问题2的完全证明将是下一步需要进行的工作。

functions with maximum algebraic immunity[J]. Information Security IET, 2011, 5(2):93-99.

[5] STANICA P, MAITRA S. Results on rotation symmetric bent and correlation immune Boolean functions[A]. Fast Software Encryption Workshop (FSE 2004)[C]. Delhi, India, 2004. 161-177.

[6] MAXIMOV A, HELL M, MAITRA S. Plateaued rotation symmetric Boolean functions on odd number of variables[A]. Proceedings of the First Workshop on Boolean Functions: Cryptography and Applications[C]. Rouen, France, 2005.

[7] ELSHEH E. On the linear structures of cryptographic rotation symmetric Boolean functions[A]. Proceedings of the 9th International Conference for Young Computer Scientists(ICYCS '08)[C]. Zhangjiajie,China, 2008. 2085-2089.

[8] XIAO G Z, MASSEY J L. A spectral characterization of correlation-immune function[J]. IEEE Transactions on Information Theory, 1988, 34(3):569-571.

[9] 李世取, 曾本胜, 廉玉忠等. 密码学中的逻辑函数[M]. 北京: 北京中软电子出版社, 2003.LI S Q, ZENG B S, LIAN Y Z, et al. Logical Functions in Cryptography[M]. Beijing: China National Computer Software and Technology Service Corporation Press, 2003.

[10] DUAN M, LAI X, YANG M, et al. Distinguishing properties of higher order derivatives of Boolean functions[EB/OL]. http://eprint.iacr.org/2010/417, 2011.