基于OFDM循环前缀LS信道估计的构造方法

赵旺兴，万群，陈章鑫

（电子科技大学 电子工程学院，四川 成都 611731）

1 引言

正交频分复用技术被认为是下一代4G或B3G无线通信系统中最关键的技术之一。该项技术的优势在于它可将一段固定频谱分隔成相互正交的子频带，提高了频谱资源利用率。同时，子频带可将小尺度衰落分割成平坦衰落，从而有效对抗多径衰落如频率选择性信道影响。结合在接收端通过信道估计和均衡，相对于单载波调制系统具有更好的传输效率。

在系统应用中，欧洲的DVB，WiMAX系统采用在频域中等间隔地插入已知导频并在接收端进行插值方法跟踪快变信道的频域信息的方式，适用于快衰落信道估计[1]。中国数字地面广播系统（DTMB）采用了一种在时域帧中插入具有不相关特征的PN序列的方式可分离出时域信道信息，已有一部分用于系统的方案中。除此之外，国内外开展了大量的理论研究工作。通常与接收端均衡联合起来研究。如在基于判决反馈的均衡方法中，将信道参数处理成滤波器抽头，用自适应的方法如最小均方法（LMS）不断训练逼近信道真实值[2]。文献[3]利用卡尔曼滤波法也属于自适应理论范畴。还有一类盲信道估计方法中，不需要借助辅助信息，直接将接收符号做数学处理，如将其变换到高阶矩阵，用特征值分解或奇异值分解再做特征提取，可以恢复出信道信息[4]。由于矩阵理论的成熟，文献[5]直接将OFDM简化为矩阵扰动模型进行分析求解。

循环前缀（CP）在抑制符号及子载波间干扰中发挥着重要的作用，一般不直接用于估计信道。尽管如此，文献[6]建立了信道估计凸优化模型。文献[7]直接推导了循环前缀与时域信道表达式的关系。文献[8]系统而全面地总结了循环前缀的完整性对信道估计及接收端均衡恢复的影响。这些方法都将循环前缀与信道估计建立了关系，不乏巧妙性。然而这些研究都是在时域上进行研究挖掘关系，很少有文献研究循环前缀的频域特性，也即将CP做相应长度的FFT变换成频域序列在频域上研究其特性。事实上，因为CP是一个OFDM最后部分的复制，它的频域序列必然携带了子载波信息。换言之，可以将其作为一种特殊的导频，并且这种导频不同于传统子载波导频对子载波信息进行局部抽取，它与子载波之间具有特殊的线性映射关系，具体见第 2节的推导。

已经有文献研究表明，与传统类似的直接占有子载波的导频序列相比，在相同的最小二乘估计准则下，CPFS法的估计均方误差（MSE）与后者具有不确定的关系。文献[9]给出了一个在LS估计框架[10]下，只要选择的子载波导频序列足够多，其信道估计的MSE一定要好于CPFS序列。那么，当选择子载波个数只能为p（CPFS点数）点时，上述2种序列进行信道估计的大小关系是值得研究的内容。

而大家熟知的在相同子载波导频选取下，有一种等间隔的子载波导频序列具有最优性，也称梳状子载波导频序列，附录 A给出了证明。那么当同时选取p点CPFS与之比较时，LS估计性能如何？通过推导它们的特征表达式，附录B将两者进行了做差比较，结果证明是不定的，取决于子载波的不同情况。

在这样的背景下，本文提出了一种构造子载波发送序列的方法，在新的构造子载波下，可使得上述2种特征序列不定的关系明朗化，利用LS信道估计的最小化 MSE机制迫使前者优于后者，从而进一步提升了LS信道估计方法的估计精度，与之对应发现了这种特殊的CPFS序列。

本文余下的部分组织如下：首先推导LS信道估计器的MSE，论述MSE取决于导频序列的能量，作为依据，推导了等间隔子载波序列与子载波发送序列间的关系并比较了两者的能量关系。在构造发送序列部分中，通过以上机制建立约束模型，用两步拉格朗日解析法解得了最优解，保证了CPFS的最优性；还对约束模型的优化进行了可行性范围分析，指出其可行性。最后用仿真验证了构造理论和约束模型的正确性。需要说明的是，⊗代表向量卷积，*代表向量之间或向量与标量间的乘积，H表示矩阵共轭转置。

2 LS信道估计器

2.1 点到点的OFDM信道传输模型

点到点的OFDM信道传输模型可表示为

其中，y代表接收端符号，s发送端符号，h时域信道，n是加性噪声。当传输过程连续时，根据傅里叶变换理论，在频域式(1)等价于

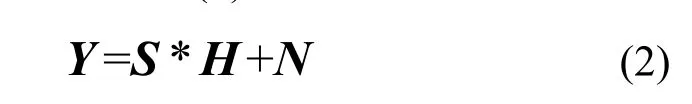
2.2 LS信道估计的最小化MSE原理

在OFDM系统中，结合式(2)，频域LS准则的信道估计表达式可简单表示为

其中，“—”表示2个向量除法，是将接收端的频域符号与发送端对应符号相除，表征LS信道估计的频域信息。结合式(2)，推导该估计方法MSE如下。

3 特征序列

为了在LS框架下比较CPFS与传统基于子载波序列信道估计的 MSE大小关系。首先定义一种等间隔子载波序列。即从子载波中等间隔地抽取出导频序列。附录A证明了在相同的点数下，其具有最小的LS估计MSE。图1给出它与循环前缀频域序列CPFS之间的关系表征。

图1 2种比较的特征序列

下面推导出2种特征序列与子载波发送序列之间的特征关系表达式。

设子载波个数为M, 训练序列个数为P，由于PM＜，于是总能够从M个子载波中抽取出P个训练序列，等间隔长度为表示向上取整。实际中，为了满足一致性条件，只要保证P略大于多径信道径数即可。

Xi, i =1,2,… ,M记为总体子载波发送序列，于是等间隔训练序列为

m表示起始训练序列位置，不失一般性，结合DFT得

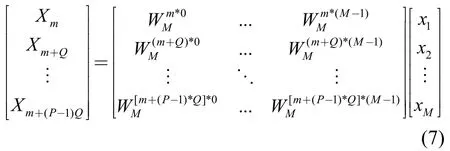
其中， fQ-1为循环前缀， ( fQ-1= xCP)，f0, … ,fQ-2表示非循环前缀部分。同理，将局部傅里叶矩阵也做相应的分块，即

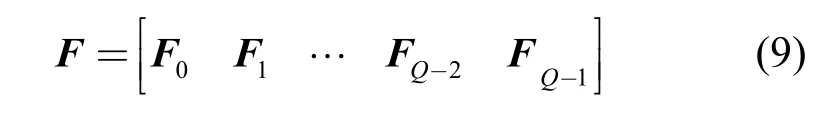
将0F化简得

观察其特征，可表示为

FP表示P点DFT矩阵。同时，进一步有

Fi= Fi-1φ, i = 1 ,… ,Q ，于是结合式(10)和式(12)得

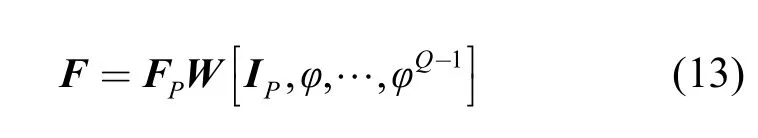
因此，

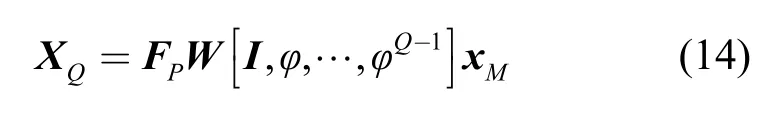
这样就得到了等间隔子载波导频序列与子载波发送序列的特征关系式。同时，直观地，循环前缀频域序列CPFS又可表示为

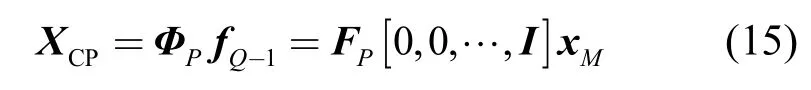
在附录B中比较了 XQ和 XCP在相同子载波下序列的能量关系，即LS信道估计器的MSE大小关系，可以证明关系是不定的。然而研究CPFS的目的是为了以之作为载体优化LS信道估计。以下从凸优化的角度，以子载波发送序列为变量，建立优化模型，解得最优的子载波发送序列，使得 CPFS能够最优化。同时，还对优化模型进行了可行域分析，论述其可行性。

4 新的发送序列构造

4.1 基本约束模型搭建

记新的发送序列为X，结合式(5)和式(14)，新的发送序列X使得2种特征序列尽量靠近，于是

同时为了使误码率不至于太大，整个发送序列与原发送序列间应尽量保持一致，即

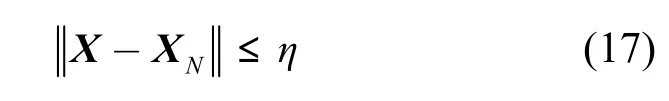
其中，η是一个很小的正数。

最后，为了使得CPFS比等间隔子载波序列的MSE小，结合式(4)和式(5)得

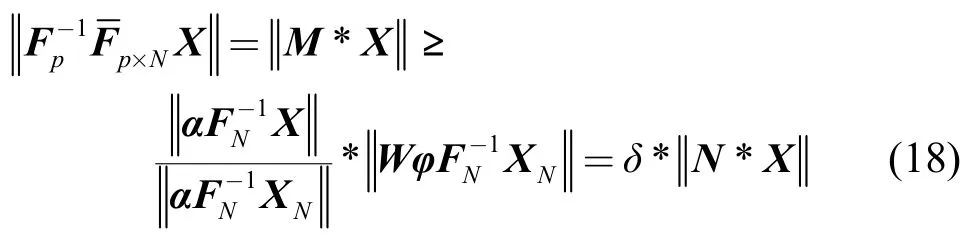
结合式(16)～式(18)，建立约束模型为

为了解得式（19）的结果，利用拉格朗日解析法求解。

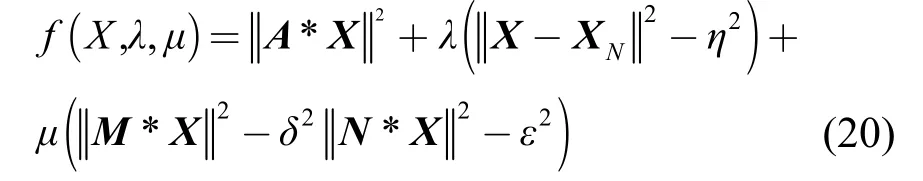
其中，λ，μ是拉格朗日约束式，ε是增量因子，由式（19）中第2个不等式引进。附录C是利用求梯度和求导的方法巧妙解出新的解X必然包含在

其中，η和ε是增量因子和确定变量。z是一个特殊的表达式，由式(18)定义。

4.2 拉格朗日重复解析

由式(21)可知，满足基本约束模型的X必然被包含在式(21)内，但是其中存在着若干解，同时为了进一步优化达到目的，有必要对结果进一步优化，与附录C一样。采用拉格朗日法进一步优化。

首先，确立一个更直观更强的目标函数，该目标函数使得构造前后2种特征序列进一步靠近。

那么，再次构造拉格朗日解析式为

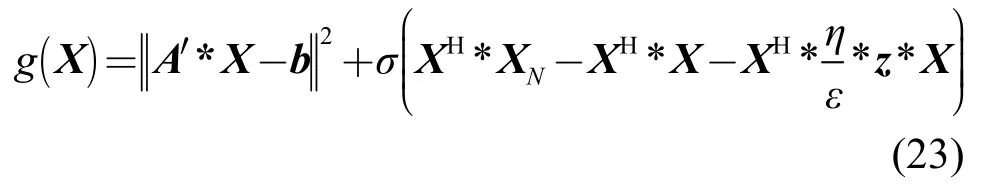
对X求梯度解得

其中，σ是拉格朗日因子。

5 构造可行性分析

第4节最后通过迭代求得最优解，为了验证以上约束优化模型具有合理性及可行性，在此继续对构造模型进行可行性分析，通过该分析从理论上可以明确构造思想的正确性。

总结起来，约束模型仅仅与2个约束式(式(17)和式(18))及2个目标函数式(式(16)和式(22))有关，并且由式(21)可知，约束式(16)与最终结果无关，因为该等式中并不包含A。因此，只需要考虑约束式(17)和式(18)及目标函数式(22)所组成的优化模型。

首先，重新抽象出约束模型，式(18)等价于

β将时域OFDM符号映射成循环前缀，α将时域OFDM符号映射为该符号带上循环前缀，γ将时域OFDM符号映射为等间隔训练序列时域符号。

同时目标函数式(22)可简记为

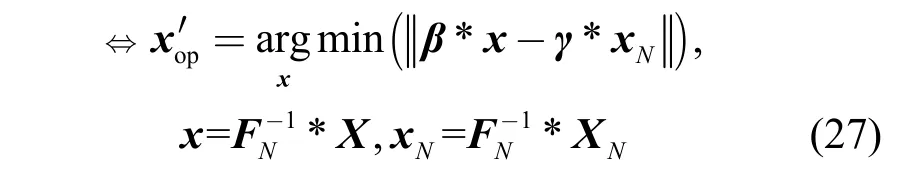
于是约束式可统一在以下框架中

在该框架下，核心是分析式(28b)的可行性。

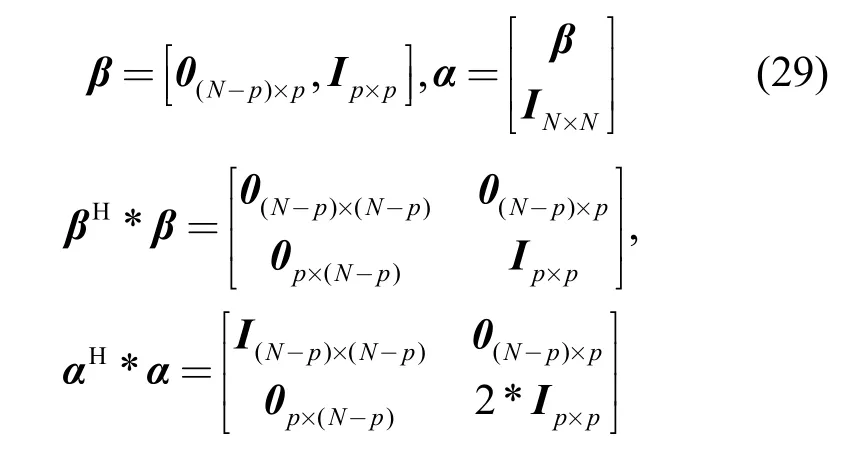
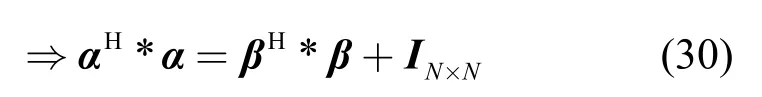
根据矩阵理论， f1(x)的范围为

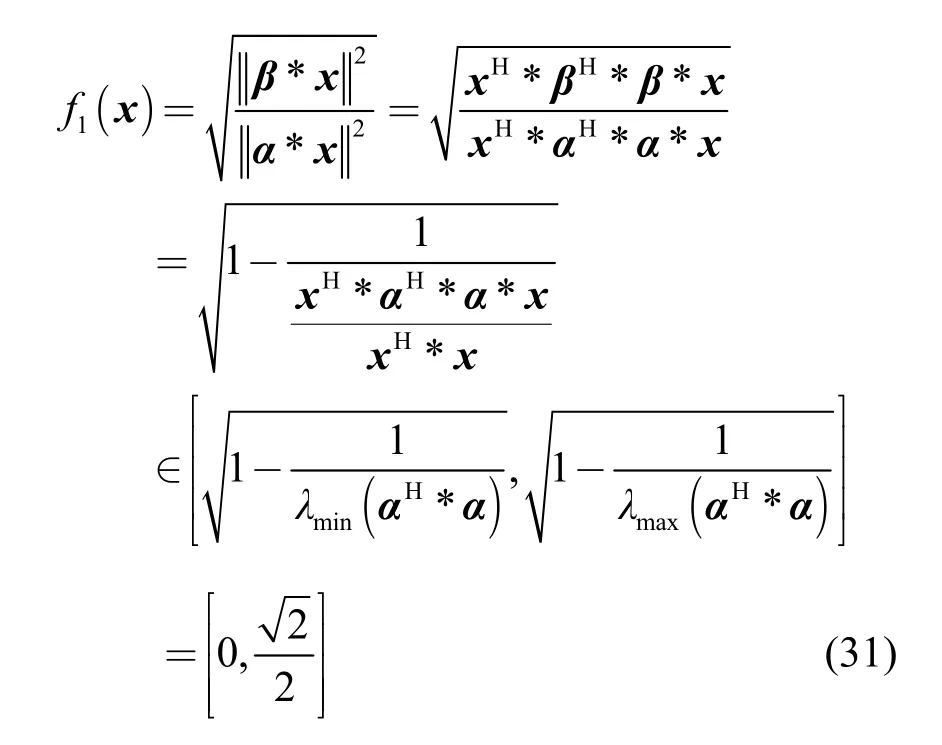
这时再构造比较函数

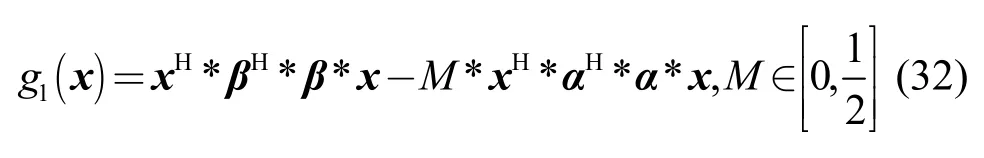
事实上，结合式（31），当M属于以上范围时，矩阵 βH* β - M* αH*α 是不定的。即存在 x0，使得 g1( x0) ≥ 0 。

接下来再计算 f2(xN)的范围，由于关系的不明朗，只能给定一个上界和下界。

其中，

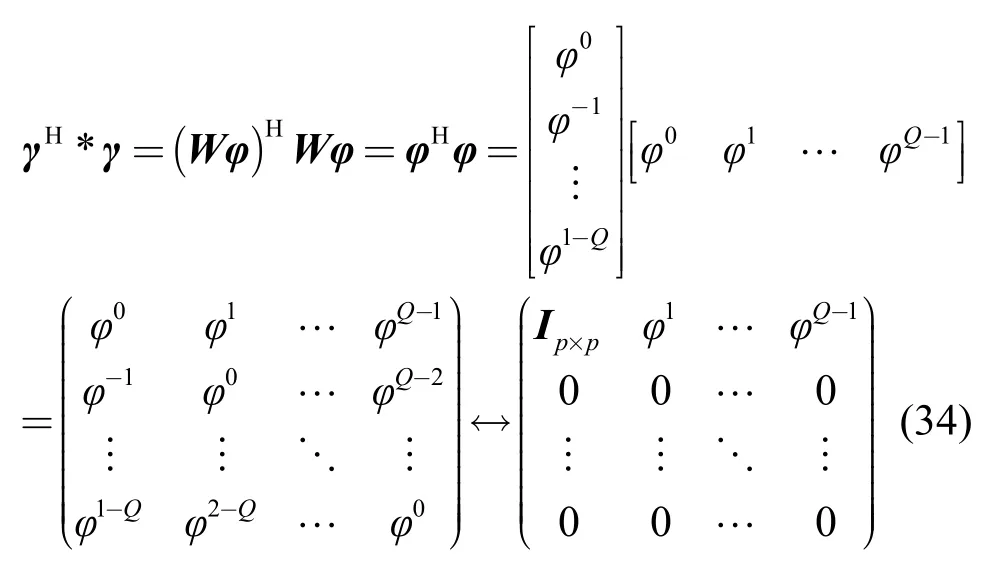
从式(34)得出如下结论。

1不可行。

事实上，这种情况等价于ε很大时，式(28b)不可能成立。然而，此时再看式(28a)和式(28c)可知，这并不影响优化结果。

6 仿真

仿真条件如下。

比特映射：16-QAM。

子载波个数：256。

是否插入导频：否。

循环前缀长度：P=16。

信道估计插值方式：DFT。

等间隔宽度：Q=16。

信道径数：H=16。

最大信噪比：40dB。

参数设置：η，ε可调。

6.1 可调参数分析

为了验证在可行性分析中的准确性，分2步对仿真理论进行验证。通过可行性分析知道，ε将影响可行性是否成立。当η固定时，首先使得作为第1种情况。然后，在第2步中设立ε很大，即足够小，逼近于0，将其作为第2种情形。

6.2 信道估计MSE分析

当 η =0.01,ε =0.01时，2种特征序列构造前后MSE结果如图2所示。

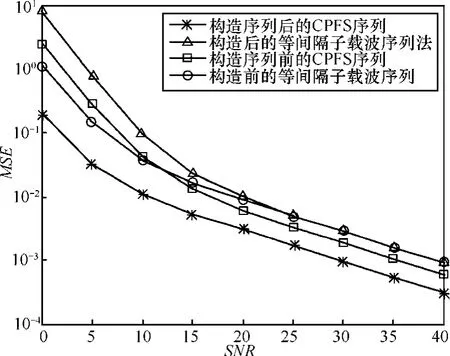
图2 基本条件下的2种特征序列构造前后MSE比较

当 η = 0 .0001,ε = 0 .1时，2种特征序列构造前后MSE结果如图3所示。

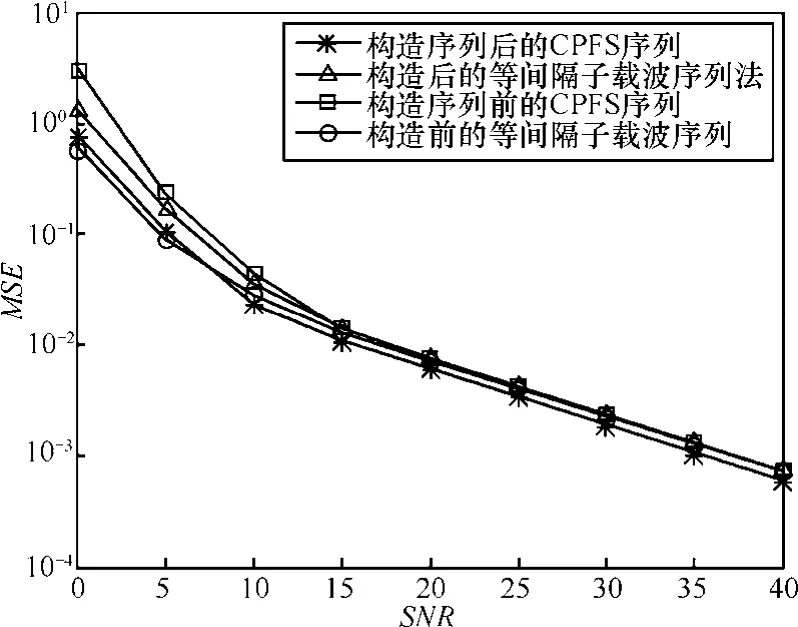
图3 拓展条件下2种特征序列构造前后MSE比较

以上仿真结果表明，可行性分析是正确无误的，从而本文的构造理论达到了预期的目的。不仅提高了LS导频信道估计的精度，也利用了循环前缀资源，提高了系统效率。

7 结束语

本文在LS信道估计框架下，提出了一种新的基于循环前缀频域序列的信道估计方法，论证了其与传统最优性的等间隔子载波序列法比较的均方误差大小关系。设计了一种构造子载波发送序列的方法，该构造方法的成功使得循环前缀LS估计方法超越了传统的具有最优性的等间隔训练序列法，达到了优化的目的。拉格朗日解析法的使用巧妙地得到了优化结果，可行性分析对优化模型进行了严格的论述，最后用仿真验证了其正确性。该设计的成功预示着，在新的 OFDM 框架下，可以充分应用循环前缀资源，同时还能够得到更准确的信道估计，从而提高了系统利用的效率。虽然构造的计算复杂度可能很高，但是作为一种理论上改进的方法，本构造理论具有很强的理论性和创新性，具有借鉴的价值和研究的意义。

附录A 等间隔训练序列最优性证明

设导频从 L个子载波中任选 p个组成导频选取下标｛k1, k2,… ,kp｝ ，那么，

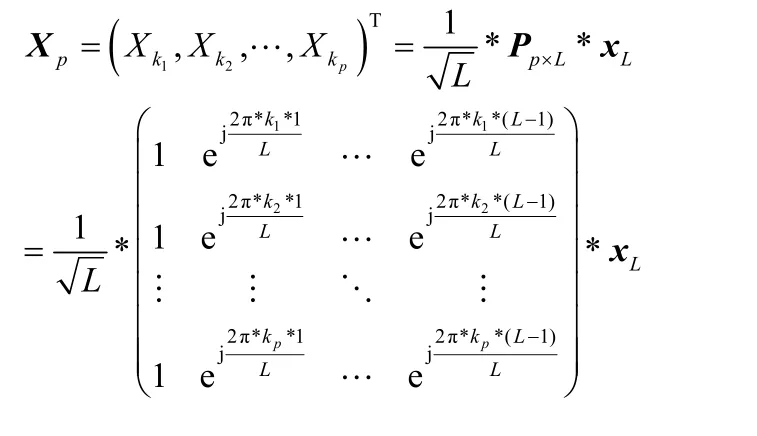
不论导频选择的哪些子载波，由式 (16)可知，决定LS通用估计器 MSE大小的因子将由矩阵Q决定，因

L×L为 xL是时域OFDM符号，相对而言是固定的。

所以矩阵LL×Q是哈密特对称矩阵，对角线上的元素为均为p，并且LL×Q可由pL×P表出，而后者秩不大于p，矩阵LL×Q的秩不大于p。

考虑将LL×Q做特征值分解如下

其中，LL×q是酉矩阵，因为pL×P是复数矩阵，所以LL×Q的特征值必然都是复数，又因为矩阵的对角线之和等于矩阵的特征值之和，以矩阵的谱范数来定义矩阵大小，所以得到如下约束关系。

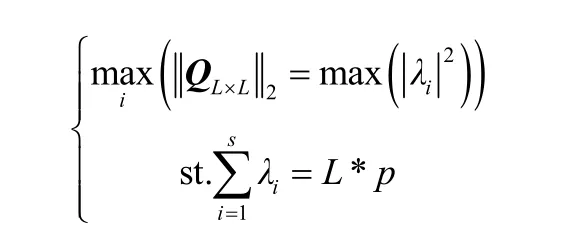
容易发现，当1s=时，LL×Q矩阵只有一个特征值或者其余特征值几乎可以忽略不计时，所有的能量都倾斜于该最大的特征值，可使得谱范数最大化。这时，矩阵LL×Q的秩理论上为1，或者每行的差距不大。又由于LL×Q是哈密特矩阵且秩为1，并且其对角线上的元素均为p，因此一个充要条件是：LL×Q的所有元素都接近p。

根据其定义，LL×Q中的第i行及第k列的元素表达式为

根据以上分析得

利用欧拉公式，进一步有

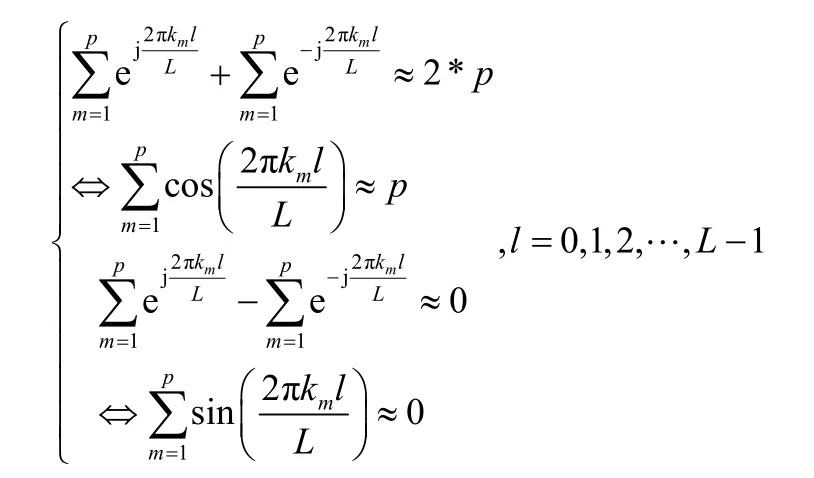
要同时满足式（21）中的条件，由于 km∈{1,2,…,L},m=1,… ,p，且l=0,1,2,…,L-1取值都要满足，于是，需要设计一种最优的km使得如下问题优化，

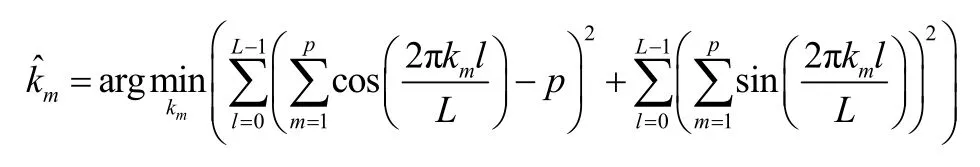
将其看作mk的函数，求偏导令其等于0，整理得

满足上式的mk只有限定其是离散均匀分布，不妨设为

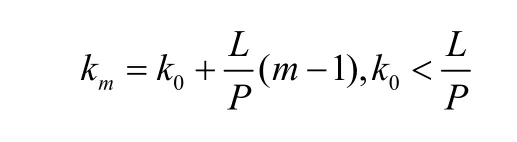
这时导频选取为等间隔的。证明完成。

附录B 2种特征序列的能量大小比较

考虑做如下变形，

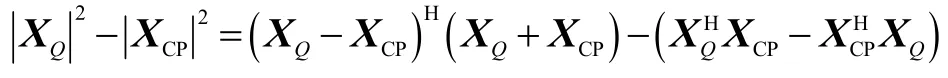
分别计算得

同时，

那么，

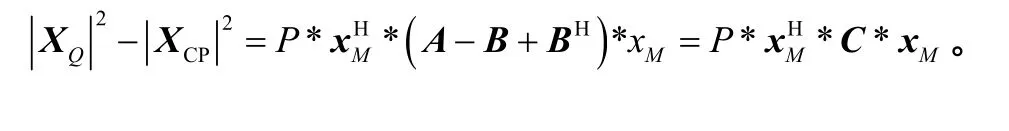
具体地，

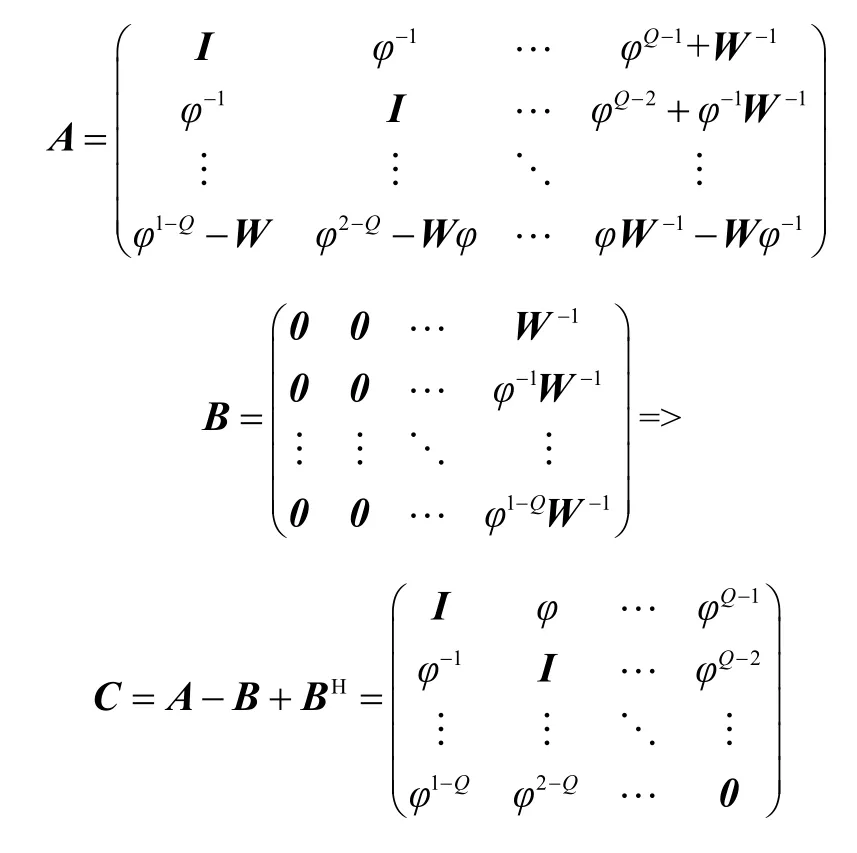
能量决定于 C, 看是否是正定或负定。首先可将C等价变形为

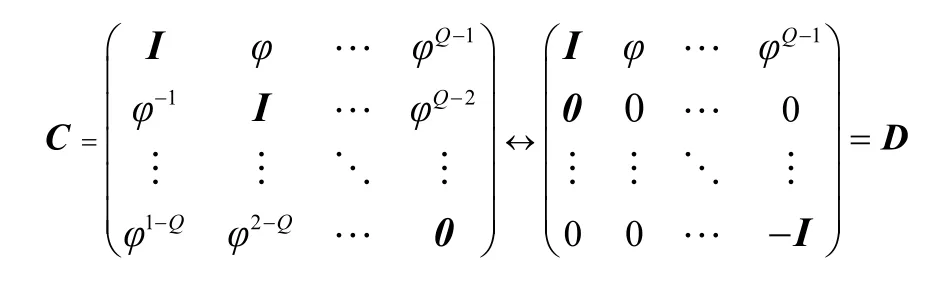
C和D等价，它们有共同的特征值，注意到D含有正和负的特征值，是不定的，从而 C是不定矩阵，意味着发送序列的不同可使得能量差可正可负，即2种特征序列的能量大小关系不定。从而2种序列LS信道估计的MSE也不定，它在相同的子载波下决定于特征序列的能量。完毕。

附录C 子载波最优解的关系式推导

对式(20)求梯度，并分别对λ和μ求导得

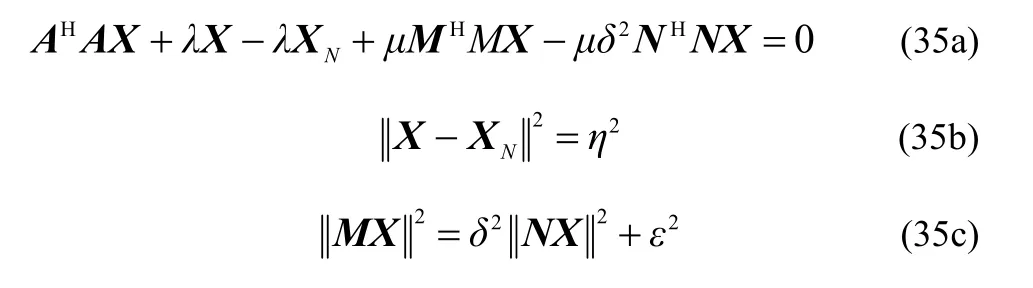
以下是具体求解过程。

首先，式(35a)可以化为

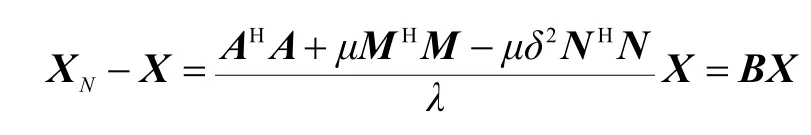
上式代入式(35b)得

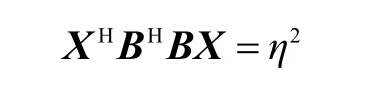
将式(35c)展开为

比较得

因为 BH=B也是一个共轭对称矩阵，所以式(36)等价于

同时，由式(35a)左乘HX 可以解出

比较式(37)和式(38)得到重要的等式

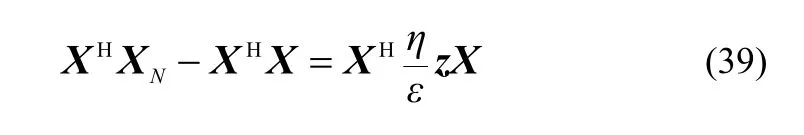
推导完毕。

[1] WANG L G, LIU H S, ZHU L X. Design methods of channel estimation device based on OFDM system[J]. Shipboard Electronic Counter measure, 2008, 31(4)：101-104.

[2] SUN G C, ZHOU C Z, SUN B. LMS adaptive channel estimation algorithm and simulation[J]. Computer Applications, 2005,25(6)：1468-1470.

[3] HE W H, LEE Y M. Low-complexity kalman channel estimator structures for OFDM systems with and without virtual carriers[A]. Proc of Communication society[C]. IEEE Press, 2004.2447-2451.

[4] KATHRYN K. Channel Estimation of Frequency Selective Channels for MIMO-OFDM[D]. Alberta：University of Calgary，2005.

[5] FENG W. Signal-Perturbation-Free Semi-Blind Channel Estimation for MIMO-OFDM Systems[D]. Montreal： Concordia University, 2009.

[6] KOIKE-AKINO T, MOLISCH A F, DUAN C J, et al. Capacity, MSE and secrecy analysis of linear block precoding for distributed antenna systems in multi-user frequency selective fading channels[J]. IEEE Trans on Communications, 2011, 59(3)：888-900.

[7] STEGER C B. Wireless Downlink Schemes in a Class of Frequency Selective Channels with Uncertain Channel State Information[D].Houston： Rice University, 2004.

[8] SU B. Blind Channel Estimation Using Redundant Precoding： New Algorithms, Analysis and Theory[D]. California： Institute of Technology Pasadena, 2008.

[9] ZHAO W X, FANG F. A diverse proof of OFDM channel estimation comparing CP-sequences and training-sequences methods under LS frame[A]. Proc of Information Theory and Artificial Intelligence Computing[C]. IEEE Press, 2011.

[10] GÜREL İ, Channel Estimation for OFDM Systems[D]. Middle East Technical University, 2005.