基于扩展Petri网的ECA规则集表示及终止性分析
张立臣,王小明,窦文阳
(陕西师范大学 计算机科学学院,陕西 西安 710062)
1 引言
基于触发机制的ECA(event-condition-action)规则能够描述主动知识,是人工智能和知识表示处理领域的研究热点[1]。应用ECA规则[2,3]和ECA规则集的动态行为特性(如可终止性、汇流性等)分析[4~10]得到研究人员的高度关注。如果从任何初始状态下开始,ECA规则集的执行过程都会在有限步之内停止,那么称ECA规则集是可终止的[4]。但是,由于ECA规则集之间存在复杂的规则结构和规则特性,如复合事件(composed event)、复合条件(composed condition)、触发关系(triggering relation)、活化关系(activating relation)和堕化关系(deactivating relation)等,导致 ECA规则集的可终止性分析问题十分困难,在考虑所有规则特性的情况下,ECA规则集的可终止性分析问题是不可判定的[5],因此,研究人员通常只考虑部分结构特性。
截至目前,在 ECA规则集可终止性分析方法中,基于图理论和基于Petri网的分析方法是主要的2类方法。触发图(TG, triggering graph)分析方法只考虑了规则间的触发关系[6],而活化图(AG, activating graph)的分析方法针对的是活化关系[7]。Baralis提出了结合TG图和AG图的终止性分析方法[8],在此基础上,Montesi定义了进化图[9],郝忠孝等提出了含环触发图的分析方法[10]。在基于图理论的分析方法中,规则用图的节点表示,规则间触发、活化或堕化关系则用图的有向边描述。若图中存在一条回路,则表明所对应的 ECA规则集是不可终止的。但是简单的图形并不能体现 ECA规则之间的细粒度规则特性(如复合事件、规则耦合模式等),导致了基于图理论的终止性分析方法的分析粒度较粗,准确性较差。
Petri网是动态系统建模和行为分析方面的形式化工具[2,3,11],被广泛应用于 ECA规则集的可终止性分析领域[12~15]。Latifa[12]基于 Petri网分析含优先级的 ECA规则集的终止性,但是没有考虑复合事件和复合条件等结构特性。Bostan-Korpeoglu[14]基于模糊有色Petri网分析模糊ECA规则集的可终止性,但只考虑了复合事件。
综上所述,现有 ECA规则集的可终止性分析方法只考虑 ECA规则之间的部分结构特性,导致算法判定的准确性较低。为了提高 ECA规则集的可终止性判定算法准确性,笔者首先提出可有效描述 ECA规则各种规则特性的扩展 Petri网(EPN,extended Petri net)模型,然后在充分利用EPN所包含的规则结构信息的基础上,综合分析 ECA规则集的可终止性,并提出了相应的可终止性判定算法,最后,通过理论分析和实验仿真对本文的算法与传统可终止判定算法进行了比较。
2 ECA规则集的EPN模型
2.1 模型设计
ECA规则的事件分为原子事件和复合事件,条件分为原子条件和复合条件。为简单起见,本文约定,ECA规则的复合事件只能通过“”∧运算符将原子事件或原子事件的“逆事件”复合起来;复合条件只能通过“”∧运算把原子条件或原子条件的否定复合而来。在此约定下,本文提出了一种可有效表示ECA规则集的扩展Petri网模型——EPN模型。
定义1 描述ECA规则集的EPN是一个9元组,EPN=(P, T, F, C, E, W, G, CF, M0)。
1) P 是库所的有限集,P=Pe∪Pt∪Pv∪Pn∪Pc,其中,Pe是事件库所集,Pt是处于触发态的库所集,Pv是处于激活态的库所集,Pn是动作库所集,Pc是条件库所集。Pe、Pt、Pv、Pn和Pc两两不相交。
2) T是变迁的有限集,Tt⊂T是触发变迁集,Tv⊂T是激活变迁集,Tn⊂T是执行变迁集。Tt、Tv和Tn两两不相交。
3) F是流关系的有限集, F = Fi∪ Fo,其中,Fi⊆ { (p, t)|p ∈ P , t ∈ T }是 输 入 弧 集 , Fo⊆{(t,p)| p∈ P , t ∈ T }是输出弧集;Fi=Fn∪Fh∪Ft,Fn、Fh和Ft分别是一般弧集(normal arcs)、抑制弧集(inhibitor arcs)和检测弧集(test arcs),并且 Fn、Fh和 Ft两两不相交。
4) C是颜色的非空有限集;CF: P→CM是颜色映射函数,其中,CM是C上的多重集(multiset)。
5) E: F→ expression 是弧函数;G: T→ bool是变迁门函数(guard function)。
6) W: P→N+是库所容量函数,对∀p∈P, 都有W(p)∈N+,N+是自然数集合,表示库所p的最大容量。
7) M0: P→CM是初始标记函数,对网中库所标记。∀p∈P,M(p)表示p的标识,p中的token以二元组(p, c)表示,其中,c∈C表示token颜色。
定义2 在EPN中,变迁t 的前集用⋅t 表示,⋅t = {p|(p, t)∈F, p∈P}。
1) 若对于∀p∈⋅t,都有 p不包含 token且(p,t)∈Fh,或者p 中至少包含E(p,t)个token,并且(p, t)∉Fh,则称t是激活的(enabled)。
2) 若t 是激活的,且G(t)返回true,则称t为可发生的(firable)。
3) 若t为可发生的,则t发生后,网中的标识由式(1)确定。

带检测弧和抑制弧的有色 Petri网在表达能力上是与传统有色 Petri网是等价的[16],因此,检测弧和抑制弧并没有降低EPN的分析能力,并且检测弧和抑制弧使得EPN比标准有色Petri网更为简洁。
2.2 EPN的描述能力
EPN不仅可以描述复合事件和复合条件,而且可以描述 ECA规则中事件消耗模式(event consumption mode)。
2.2.1 对触发变迁的描述
ECA规则的每个原子事件在EPN中都对应一个原子事件库所。普通原子事件在EPN中对应的事件库所与触发变迁之间的弧是普通弧,而原子事件的“逆事件”对应的弧则为抑制弧。设一条ECA规则r的事件为e1∧e2∧¬e3,变迁t是r在EPN中对应的触发变迁,库所p是r处于触发态的库所。图1是触发变迁t发生过程,图1(a)是t发生前EPN状态,图1(b)是t发生后EPN状态。t发生后,一个token将流入到库所p,其含义是规则r被触发。
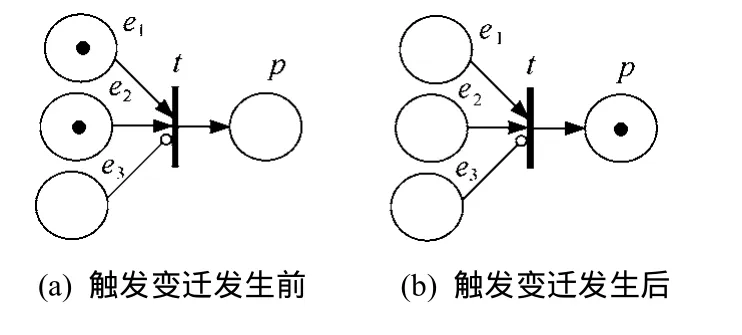
图1 触发变迁的发生过程
2.2.2 对激活变迁的描述
ECA规则的每个原子条件在EPN中都对应一个条件库所。普通原子条件所对应的条件库所与规则的激活变迁之间的弧是检测弧,而否定形式的原子条件所对应的条件库所与激活变迁之间的弧是抑制弧。设一条ECA规则r的条件为c1∧¬c2,变迁t为激活变迁,库所p和p'分别为处于触发态和激活态的库所。激活变迁t的发生过程如图2所示,其中,图2(a)是t发生前的EPN状态,图2(b)是t发生后的 EPN状态。t发生后,p'中将产生一个token,此时规则r被激活。
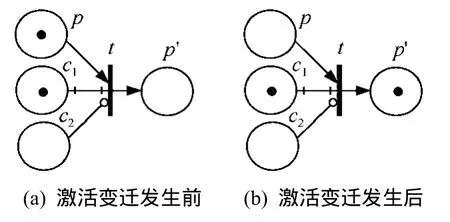
图2 激活变迁的发生过程
2.2.3 对执行变迁的描述
通常情况下,一条 ECA规则执行后不会产生事件,也不会改变条件,此时该规则在EPN所对应的执行过程如图3所示,其中,库所p和p'分别为处于激活态的库所和动作库所。
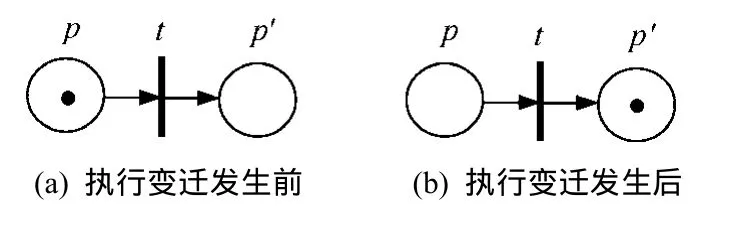
图3 执行变迁的发生过程
2.2.4 对规则动作改变条件情形的描述
如果一条ECA规则r改变原子条件,那么EPN中r对应的执行变迁t的发生过程如图4所示,其中,库所p和pc分别为处于激活态的库所和条件c
对应的库所。
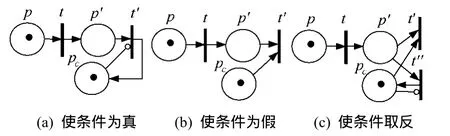
图4 3种改变条件的情形对应的EPN
1) 情形1:使条件c为真
如图4(a)所示,在网中添加一个动作库所p'和一个变迁t',(pc, t')为抑制弧。t发生后,如果c为真,则t'将不发生,此时c仍为真;否则t'将发生,将c改为真。
2) 情形2:使条件c为假
如图4(b)所示,在网中添加一个动作库所p'和一个变迁t',(pc, t')为一般弧。t发生后,如果c为假,则t'将不发生,此时c仍为假;否则t'将发生,将c改为假。
3) 情形3:使条件c取反
如图4(c)所示,在网中添加一个动作库所p'和2个变迁t'和t'',(pc, t')和(pc, t'')分别为一般弧和抑制弧。t发生后,如果c为真,则t'将发生,将c改为假;否则变迁t''将发生,将c改为真。
2.2.5 对事件消耗模式的描述
ECA规则的事件消耗模式包括消耗范围(记为cs)和消耗时间(记为 ct)2种属性[17],其中,消耗范围表示系统对触发事件的处理方式,具有3种取值:不消耗(记为0)、局部消耗(记为1)和全局消耗(记为2);消耗时间属性有2种取值:条件评价后(记为0)和规则动作执行后(记为1)。若ct=0,则不考虑条件评价的结果,而是根据cs的取值处理触发事件;若ct=1,则需考虑规则条件评价结果。如果条件评价结果为假,则不处理触发事件;否则,将根据cs的取值处理触发事件。为了在EPN中有效描述事件消耗模式,本文约定,对于一个事件库所 p,其中的token标识(p, c)中c取值为规则标识,含义是该token能够触发规则标识为c的ECA规则。针对不同的事件消耗模式,EPN的具体结构如下:(设事件 e是可以触发规则集{rj, rj+1, …, rk},p是对应的事件库所)
1) 消耗范围是不消耗(cs=0)
此时,p中有一个标记为(p, n)的token,符号n表示 e的事件消耗范围是不消耗;p到规则集{rj,rj+1,…, rk}所对应的每一个触发变迁均有一条输入弧。图 5是事件消耗时间为“条件评价后”(ct=0)的EPN结构,t2是激活变迁。设r的条件为c1∧¬c2。pc1和 pc2分别与变迁 t3和 t4连接,其中,( pc1, t2)和( pc2, t4)为检测弧,( pc1, t3)和( pc2, t2)为抑制弧。r被触发后,3个变迁t2、t3和t4中有且仅有一个发生,此时,库所p中都将产生一个token,其含义是当评估完条件后,触发事件e都将重新产生,而不论评估结果如何。
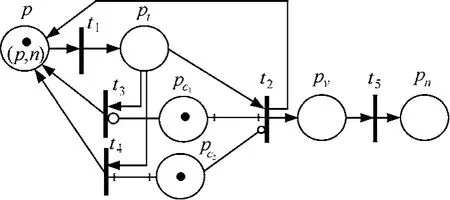
图5 触发事件的消耗范围为“不消耗”且ct=0时的EPN
图 6为事件消耗时间为“执行动作后”(ct=1)的EPN,t2和t3分别是激活变迁和执行变迁。只有当t3发生时,e才会被重新产生,其含义是在条件的评价结果为真时,不会被消耗触发事件,反之,若条件检测结果为假,则消耗触发事件。
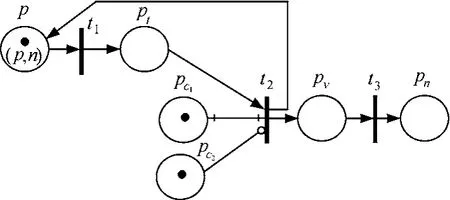
图6 触发事件的消耗范围为“不消耗”且ct=1时的EPN
2) 消耗范围是局部消耗(cs=1)
此时,事件库所p中有k-j+1个token,标记分别为(p, rj), (p, rj+1), …, (p, rk)。库所 p到{rj,rj+1, …, rk}所对应的每个触发变迁均有一条输入弧,且弧上的表达式为所指向的 ECA规则标识。由于每个token根据其颜色只触发其中一条规则,因此,局部消耗事件在消耗时间为“条件评价后”与 “执行动作后”的EPN结构相同。图7为局部消耗模式的EPN,设规则r1的条件为c1˄c2, t2和t3分别是激活变迁和执行变迁,不论t2是否发生,触发事件都将被消耗。
3) 消耗范围为全局消耗(cs=2)
此时,库所 p中只有一个标记为(p, g)的token,符号 g 表示事件消耗范围是全局消耗;p到{rj, rj+1,…, rk}的每个触发变迁均有一条输入弧。设e触发了2条ECA规则r1和r2,其中,r1优先级较高,r1和r2的条件分别为c1和c2。图8为事件消耗时间为“条件评价后”(ct=0)的 EPN,t2和 t3分别是 r1和r2的激活变迁。t1发生后,r1和r2被触发。由于(1tp, t3)是抑制弧,故先评价c1。若c1满足,则消耗2tp中的token,处于触发态r2被改成未触发态。
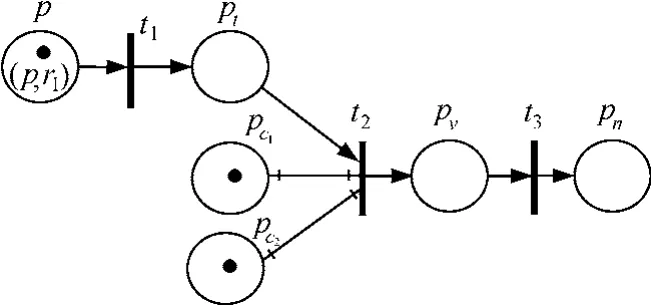
图7 触发事件的消耗范围为“局部消耗”的EPN
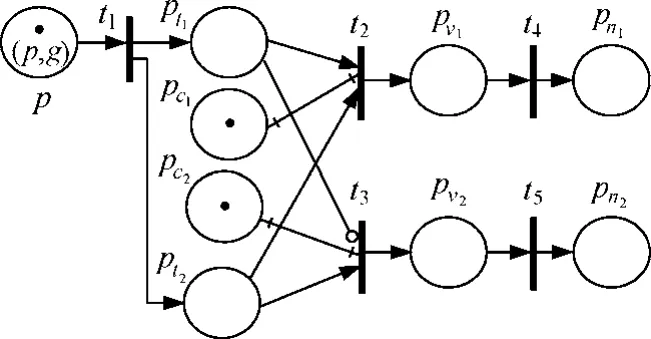
图8 触发事件的消耗范围为“全局消耗”且ct=0时的EPN
图 9为触发事件的消耗时间为“执行动作后”(ct=1)的EPN。t1发生后,r1和 r2均被触发,此时(1tp, t3)和(1vp, t3)是抑制弧,因此先对r1进行条件评价,当r1的条件满足且变迁t4发生时,r2的状态被改变,被重新转为未触发状态。
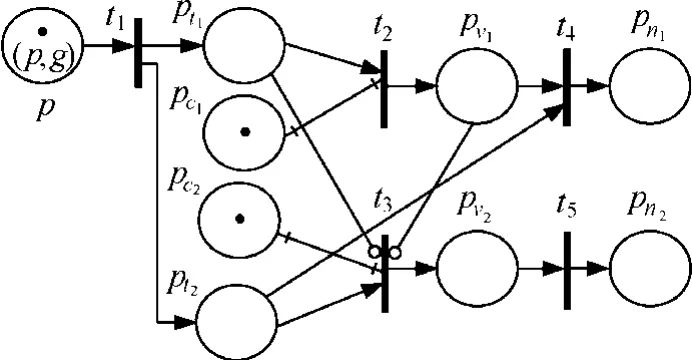
图9 触发事件的消耗范围为“全局消耗”且ct=1时的EPN
2.2.6 对规则产生事件的描述
在EPN中,如果执行变迁产生原子事件e(设p为e对应的事件库所),那么:1) 如果e的事件消耗模式为不消耗,则所产生 token的标记为(p,n);2) 如果 e的事件消耗模式为全局消耗,则所产生token的标记为(p, g);3)如果e的事件消耗模式为局部消耗,设e可触发规则集{rj, rj+1,…, rk},则将产生k-j+1个token,其标记依次为(p, rj), (p,rj+1),…, (p, rk)。
2.3 EPN举例
例1 一条ECA规则r 描述如下。
ON e1˄e2˄¬e3
IF c1˄¬c2THEN e2˄¬c1
规则 r 的语义为:当原子事件e1和 e2发生并且e3没有发生时,r被触发,然后评价r的条件,如果c1成立且c2不成立,则执行动作,产生e2并使c1不成立。设r触发事件的消耗模式为局部消耗。图10是规则r的EPN的初始状态,e1和e2已发生,e3未发生,此时触发变迁t1是可发生的。t1发生后,r被触发,库所pt中产生一个token。由于条件库所pc1中有 token(条件 c1成立)且库所 pc2中没有token(条件c2不成立),此时激活变迁t2是可发生的。t2发生后,r被激活,库所pv中产生一个token。此时,t3可发生。t3发生后,在e3和pn各产生一个token。由于1cp有token,因此变迁t4是可发生的。t4发生后,消耗库所1cp中的token。此时,完成了规则r 的一次触发执行过程。
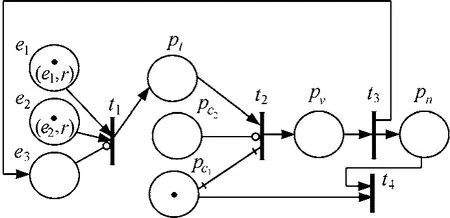
图10 规则r的EPN
2.4 ECA规则集的EPN等价转化
为了利用 EPN中的规则结构信息分析规则集的终止性,本文提出了EPN的等价转化算法,该算法将包含复杂规则特性(如复合事件、复合条件、事件消耗模式、触发关系、活化关系和堕化关系等)的ECA规则集转化为等价的EPN。ECA规则集EPN的等价转化算法如图11所示。
3 ECA规则集的终止性分析
3.1 理论分析
在ECA规则中,如果存在事件消耗模式为不消耗的事件,那么一旦该事件发生,该规则将不可终止。因此本文假设规则集中不存在事件消耗模式为不消耗的规则。设∑为 ECA规则集R的EPN表示,L是网∑ 中的一个触发环,L=(r1, r2,…, ri)表示规则 r1触发 r2, r2触发 r3,…,且 ri触发 r1。

图11 ECA规则集EPN的等价转化算法
定义3 设L是网∑的一个触发环,如果从任意初始标识出发,L中的规则都将在执行有限次后永远不会被触发,那么称L为一个假触发环,否则,L为一个真触发环。
定义4 设L是网∑的一个触发环。对于L中的一条规则r和一个库所p,如果规则r在网∑中对应的事件库所集合、条件库所集合和动作库所集合包含p,则称p属于触发环L,记p∈L。
定义5 设L是网∑的一个触发环,如果存在库所p和p',满足p∈∑,p'∈L,并且从库所p'到库所p有一条通路,则称p是触发环L可达的。
定理1 设L是网∑中一个触发环,存在一条规则r∈L,构成规则r的原子事件设为e,并设e在∑中对应的库所为p,t为规则r的触发变迁。如果(p,t)为一般弧,满足要么p的前集为空,要么p不由任何触发环可达,那么L是一个假触发环。
证明 设网∑的一个触发环L=(r1, r2, …, ri)且规则r∈L,e是r的原子事件,p为e对应的事件库所,t为r的触发变迁,(p, t)为一般弧,n为∑的初始标识下p中所包含token的数目,n是自然数。1)如果 p的前集为空,那么∑中任何变迁的发生只可能消耗p的token,而不会在p中产生token。消耗完所有p中的token以后,规则r 将不可能被再一次触发和执行。由于初始状态下p中的token的数目是有限的(数目为n),因此,r 最大触发次数不会超过n,在此之后,r 将不能再被触发,从而L为一个假触发环。2) 如果p不被任何触发环可达,此时进入p中的token数目是有限的,不妨设为m,从而当消耗完p中所有token时,r被触发执行的次数不会超过n+m。此后规则r将不能再被触发,从而L终止。
因此,触发环L是一个假触发环,命题得证。
推论1 设L是网∑中一个触发环,一条ECA规则r∈L,e为r的原子事件,p为e对应库所,t为r对应的触发变迁,弧(p, t)为一般弧。如果p的前集为空或仅由假触发环可达,则L是一个假触发环。
定理2 设L是网∑中一个触发环。如果存在一条ECA规则r∈L,其原子条件为c,满足以下3个条件:1) (c, t)是一般弧,其中,t是r的激活变迁;2) c被改为假或取反;3)改变c 的规则只有一条,设为r',且r'∈L,那么L为一个假触发环。
证明 采用反证法。假设触发环L不是假触发环。此时,从∑中任何状态出发,r' 可以被无限次执行。规则 r'改变了规则 r的条件 c,使其为假或取反,但是r被激活的前提是条件评估必须为真。由于改变规则r条件的规则只能是规则r',因此当r'执行后,导致规则r的条件评价为假,从而使得r不能被激活和执行,从而使得L不能永远执行下去,与假设矛盾。命题得证。
定理3 设L是网∑中一个触发环,如果存在一条ECA规则r∈L,r的原子条件为c,并且1) (c, t)是抑制弧,其中,t是r的激活变迁;2) c被改为假或取反;3) 改变c的规则只有一条,设为r',且r'∈L,那么L为一个假触发环。
证明 与定理2类似。
定理4 设ECA规则集R的等价EPN为∑,如果∑中不存在任何触发环或者所有的触发环都是假触发环,那么,ECA规则集R是可终止的。
证明 如果网∑中不包含任何触发环,则命题显然成立。设L是∑的一个假触发环,那么对于任意ECA规则r∈L,由定义3可知,r在触发有限次后将不能被再次触发,导致规则r是可终止的。由于∑中所有触发环都是假触发环,因此,规则集 R中的所有假触发环中的规则都是可终止的,从而R是可终止的。命题得证。
3.2 终止性判定算法
基于ECA规则集的等价EPN,本文提出了相应的终止性判定算法。该算法充分利用EPN所包含的规则信息,通过化简EPN来判定规则集的可终止性。算法具体描述如图12所示。

图12 ECA规则集的可终止性判定算法
本质上讲,基于图理论的 ECA规则集终止性分析方法是通过构造规则集的触发关系矩阵(或活化关系矩阵等),并依据该矩阵元素的可达性判定原规则集是否存在环(回路)。一般地,设A为规则集的触发关系矩阵,元素aij=1表示ECA规则i触发ECA规则j。矩阵M=Ak中的元素mij的值表示从规则i到规则j的长度为k的触发链路条数,而其对角线上的元素aii不为0则表示存在触发环或回路。在极端情况下,规则集不存在任何触发环或存在一个包含大部分或所有规则的触发环时,矩阵的乘法运算需要进行到An,这是判定算法的最坏情况。因此,现有基于触发图等图理论的判定算法的时间复杂度为O(n4)[8,9,14],其中,n为ECA规则条数。
本文提出的规则集判定算法不同于传统基于图理论的规则集可终止性判定算法,它基于ECA规则集的等价EPN,而EPN中包含了ECA规则的丰富规则信息,如复合事件、复合条件、事件消耗模式等,通过在EPN来判定定理1、定理2和定理 3,从而不断消除所有能终止的规则和所有假触发环,达到化简 EPN的目的。如果最终EPN的所有元素均被删除,则表示原ECA规则集不包含任何触发环或所有的触发环都是假触发环,从而原ECA规则集是可终止的,否则,原规则集不可终止。
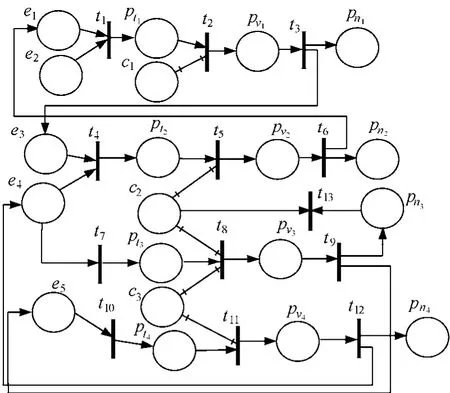
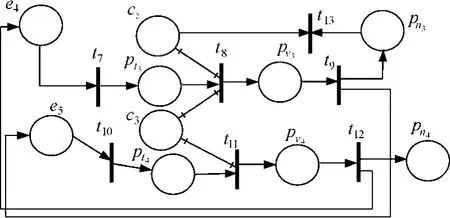
在算法2中,2)基于定理1和推论1对EPN进行化简,时间复杂度为O(m2),其中,m为ECA规则集中所有不同的原子事件个数。3)基于定理2和定理3对EPN再次化简,时间复杂度为O(kn),其中,k为规则中所有原子条件的个数,n为规则条数。通常在ECA规则集合中,k< 例2 设有ECA规则集R={ r1, r2, r3, r4},其中, r1: ON e1˄e2IF c1THEN e3 r2: ON e3˄e4IF c2THEN e1 r3: ON e4IF c3˄c2THEN ¬c2˄e5 r4: ON e5IF c3THEN e4 ECA规则r1, r2, r3和r4中各元素的含义与例1中的 ECA规则相同,设所有规则的事件消耗模式为局部消耗。图13是规则集R的等价EPN∑。对规则集R的终止性分析过程如下所述。 图13 规则集的EPN 执行算法2的2)后,网∑被化简,如图14所示。在3)中,由于原子条件c2及改变该条件的唯一一条ECA规则r3使c2为假,从而定理2成立,进而删除相关元素后,EPN被再次化简为只剩下规则r1。由于flag的取值为true,转至2),EPN被再次化简为空,从而得出结论:规则集R是可终止的。目前,采用已有方法均不能得出与笔者相同的终止性分析结论。 图14 化简后的EPN 针对不同的ECA规则集和终止性判定算法,本文设计了相应的仿真实验以验证各判定算法的正确性和效率。实验环境如下:CPU Intel 双核1.86 GHz,内存 1GB,Windows XP专业版,Microsoft Visual Studio 2005平台。参与对比的判定算法有3种TG、BK和PN算法,其中,TG(基于触发图的判定)算法是依据规则集的触发关系矩阵及其乘法运算计算是否存在回路,BK 算法是 Bostan-Korpeoglu[14]等人的算法,PN是本文所使用的算法。 待测试ECA规则集R只包含一个触发环L,L= {r1, r2, …, rn},n为规则条数。r1的事件为 e1˄e2,rn产生事件e1、事件e2是独立事件,它不被任何规则产生。实验中n取值范围(100, 1 000)。表1记录了规则集在不同算法下的运行时间。结果表明本文提出算法(PN)的效率最高,且算法PN和BK得出了正确结论(规则集是可终止的),而算法 TG的判定结果出错(规则集不可终止)。 表1 含一个触发环时算法的运行时间(单位:s) 待测试ECA规则集R含有3个触发环,分别为 L1、L2和 L3,其中,L1=( r1, r2,…, rn/2),L2=( rn/2+1,rn/2+2,…, rn)和 L3=(rn/4, rn/4+1,…, rn/2, rn/4×3, rn/4×3+1,…,rn)。规则 r1的事件为 e1˄e2,其中,e2不被任何规则动作产生。表2记录了规则集在不同算法下的运行时间,结果表明本文提出算法(PN)的运行时间仍然最短,并且得出了正确结论,而TG算法的判定结果仍然是错误的。 表2 含3个触发环时算法的运行时间(单位:s) 随机生成待测试ECA规则集R。表3记录了不同算法的运行时间。所有算法的判定结果是规则集保证终止,即规则集不含任何触发环,但本文算法PN的运行时间仍远低于其他算法。 表3 不同算法对随机生成的规则集判定的运行时间(单位:s) ECA规则具有复杂的结构特性,这些结构特性使得 ECA规则集的可终止性判定十分困难。针对目前 ECA规则集的终止性判定算法只考虑部分结构特性而导致算法准确性差的缺点,本文提出了可有效表示ECA规则集的扩展Petri网模型(EPN),并在此基础上综合分析了 ECA规则的各种结构特性对终止性的影响,提出了基于EPN的可终止性判定算法。该算法通过化简EPN来直接删除ECA规则间的假触发环,从而提高了判定准确性,并在一定程度上降低了传统图理论判定算法的时间复杂度。理论分析和实验结果表明,本文提出的 ECA规则集可终止性判定算法具有更高的准确性和更低的时间复杂度。 [1] PATON N, DIAZ O. Active database systems[J]. ACM Computing Surveys, 1999, 31(1):63-103. [2] 卢捍华, 闵丽娟, 王亚石. 工作流主从实例处理方法及其Petri网建模[J]. 通信学报, 2010, 31(1):92-99.LU T H, MIN L J, WANG Y S. Approach to master-slave workflow system and its Petri-net modeling[J]. Journal on Communications,2010, 31(1):92-99. [3] 郭迎九, 林闯, 尹浩等. 基于Petri网的数字媒体分发协议的安全性证明[J].电子学报,2009,37(5):1031-1036.GUO Y J, LIN C, YIN H, et al. Proof of the security of digital media distributing protocol based on Petri net models[J]. Acta Electronica Sinica, 2009, 37(5):1031-1036. [4] AIKEN A, WIDOM J, HELLERSTEIN J M. Behavior of database production rules: termination, confluence, and observable determinism[J]. SIGMOD, 1992, 21(2):59-68. [5] BAILEY J, DONG G, RAMAMOHANARAO K. Decidability and undecidability results for the termination problem of active database rules[A]. PODS'98[C]. New York, USA, 1998. 264-273. [6] MURATA T. Petri nets: properties, analysis and applications[J]. Proceedings of the IEEE, 1989, 77(4):541-580. [7] BARALIS E, CERI S, WIDOM J. Better termination analysis for active databases[A]. RIDS '93[C]. Edinburgh, Scotland, 1993.163-179. [8] BARALIS E, CERI S, PARABOSCHI S. Improved rule analysis by means of triggering and activation graphs[A]. RIDS'95[C]. Greece:Springer-Verlag, 1995. 165-181. [9] MONTESI D, BAGNATO M, DALLERA C. Termination analysis in active databases[A]. IDEAS'99[C]. Montreal, Canada, 1999. 288-297. [10] 郝忠孝, 任超, 赵龄强. 含环触发图对应的主动规则集可终止性分析[J]. 计算机研究与发展, 2005, 42(12):2199-2205.HAO Z X, REN C, ZHAO L Q. Termination analysis of active rule based on dependency set[J]. Journal of Computer Research and Development, 2005, 42(12):2199-2205. [11] 熊曾刚, 杨扬, 曾明. 基于Petri网的两阶段网格任务调度模型与分析[J]. 通信学报, 2009, 30(8):69-77.XIONG C G, YANG Y, ZENG M. Research on two-phase grid task scheduling based on Petri nets[J]. Journal on Communications, 2009,30(8):69-77. [12] LATIFA B, HAFIDA B. The priority of rules and the termination analysis using Petri nets[J]. The International Arab Journal of Information Technology, 2007, 4(2):177-183. [13] MEDINA-MARIN J, PEREZ-LECHUGA G, LI X. ECA rule analysis in a distributed active database[A]. ICCTD'09[C]. Kinabalu, Malaysia,2009.113-116. [14] BOSTAN-KORPEOGLU B, YAZICI A. A fuzzy Petri net model for intelligent databases[J]. Data & Knowledge Engineering, 2007, 62(2):219-247. [15] 张立臣.面向普适计算的主动访问控制模型研究[D].西安:陕西师范大学,2011.ZHANG L C. Research on Active Access Control Model for Pervasive Computing[D]. Xian: Shaanxi Normal University,2011. [16] CHRISTENSEN S, HANSEN N. Coloured Petri nets extended with place capacities, test arcs and inhibitor arcs[J]. Lecture Notes in Computer Science, 1993, 691(1):186-205. [17] FRATERNALI P, TANCA L. A structured approach for the definition of the semantics of active databases[J]. ACM Trans on Database Systems, 1995, 20(4):414-471.3.3 终止性判定举例
4 实验分析
4.1 实验1
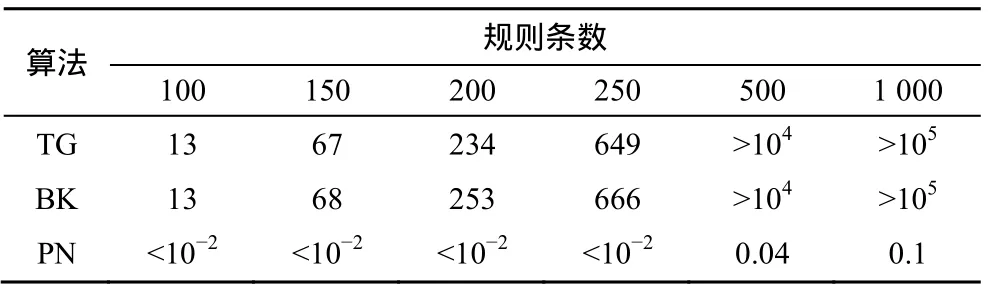
4.2 实验2
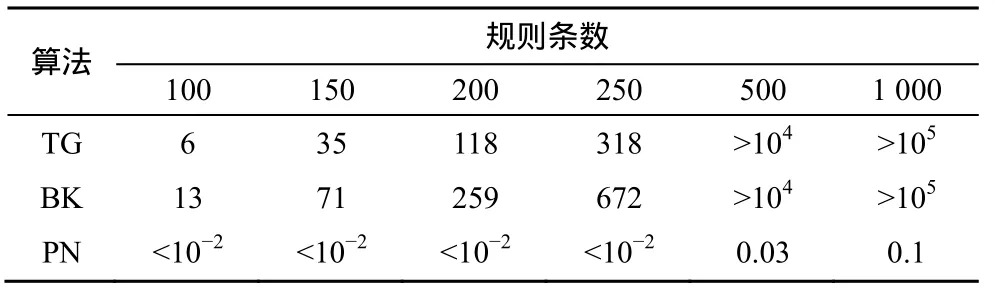
4.3 实验3
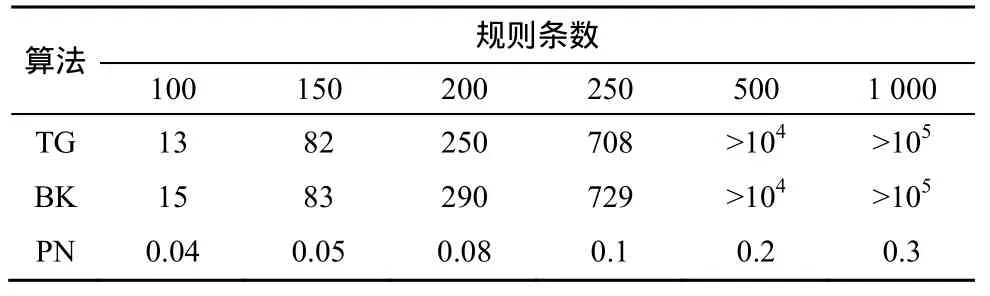
5 结束语

