无损分享视觉密码研究
郁滨,付正欣
(信息工程大学 电子技术学院,河南 郑州 450004)
1 引言
视觉密码[1](visual cryptography)是一种新的图像分存技术,它将秘密共享和数字图像相结合,经过 10多年的不断丰富和发展,已经成为密码学的一个新的研究方向,并从最初的(2, 2)方案发展成为一个相对完善的理论体系。
视觉密码通过秘密分享算法将秘密图像编码成为若干个共享份,并分发给每个参与者。当参与者集合满足约定的恢复条件时,只需将参与者的共享份直接叠加即可恢复出秘密图像。由于视觉密码的秘密恢复过程简单,因此视觉密码的研究重点主要集中于秘密分享算法。
以基矩阵为核心的秘密分享算法由 Naor和Shamir最先提出,由于其能够保证视觉密码方案的安全性和对比性条件,因而基矩阵的设计是视觉密码方案的关键。Naor和Shamir[1]证明了(n, n)方案的最小像素扩展度为 2n-1,并给出了基矩阵的构造方法,即B0(分享白像素的基矩阵)由所有汉明重量为偶数的列向量组成,B1(分享黑像素的基矩阵)由所有汉明重量为奇数的列向量组成。Bludno等[2]证明了(2, n)门限方案的最小像素扩展度为满足的最小 m值,在基矩阵设计时,B0由n个相同的汉明重量为 ■ m 2■的行向量组成,而 B1由 n个不同的汉明重量为 ■ m 2■的行向量组成。Droste[3]提出了ADD算子,用以在(n, n)方案基础上动态增加列向量,可以有效地减小(k, n)门限方案的像素扩展度,同时还提出利用线性规划的方法设计基矩阵,但由于规划模型的解不是整数,因此并不具有实际的意义。Ateniese等[4]通过定义授权集合QualΓ和禁止集合ForbΓ,将视觉密码由门限结构扩展到通用存取结构,并提出了2种经典的基矩阵构造方法,即基于累积矩阵方法和小方案扩展方法,广泛地应用于通用存取结构的方案。Hajiabolhassan[5]研究了几种特殊的通用存取结构,讨论了其像素扩展度的界限,并提出了相应的基矩阵设计方法。研究表明,基矩阵的列数代表图像面积上扩大的倍数,而以基矩阵为核心的视觉密码方案无法达到像素扩展度的理想值“1”。
为了使像素扩展度达到理想值,部分学者提出了与基矩阵不同的秘密分享算法。Yang[6]以整幅图像的安全性代替每个像素点的安全性,在分享像素点时随机从基矩阵中选取一列,实现了像素的不扩展。白璟霖[7]利用随机乱数率表示图像的对比度,提出了一种基于随机数的秘密分享算法,实现了像素的不扩展。Hou等[8]利用人类视觉系统的空间均衡及局部统计等特性,提出了一种多点加密法,该方法可以一次分享m个像素,使像素扩展度达到了理想值。Hsu等[9]从概率的角度研究视觉密码方案,认为原图像的识别可以通过黑白区域的不同灰度来实现,设计了以加密规则矩阵和概率矩阵为核心的秘密分享算法,得到了像素扩展度为1的视觉密码方案。上述方案达到了像素扩展度的理想值,但均以原图像的信息损失为代价,即恢复图像不再包含原图像的所有信息。目前尚无像素扩展度与信息损失之间关系的研究。
针对像素扩展与信息损失的问题,本文给出了无损分享的定义,指出无损分享视觉密码的最优像素扩展度是区分无损分享与有损分享的关键,并设计了矩阵转化算法和整数规划模型,实现了一种像素优化算法,可以在保持恢复计算复杂度的条件下实现完全恢复。
2 无损分享
设 P = { 1,… ,n }表示 n个参与者的集合,2p表示P的所有子集组成的集合。记ΓQual为授权集合,ΓForb为禁止集合,其中, ΓQual⊆2p, ΓForb⊆2p,且 ΓQual∩ ΓForb= Ø ,则(ΓQual,ΓForb)表示一个视觉密码方案的通用存取结构。下面是以基矩阵为核心的视觉密码方案定义。
定义1[4]( Γ ,Γ)为参与者集合P = { 1,…,n}
QualForb
的通用存取结构,称 ( ΓQual, ΓForb,m)-VCS表示一个视觉密码方案,其基矩阵为n×m的布尔矩阵B0和B1。当分享白(黑)像素时,选择 B0(B1)进行随机的列排序,以确定n个共享份中m个子像素的颜色。B0和B1满足以下2个条件。
1) 对比性条件:对于授权子集 X ={i1, i2, … ,ip}∈ ΓQual,B0的 i1, i2, … ,ip行“或”运算得到的向量V满足 H ( V)≤ tX-αm;B1的i1, i2, …, ip行“或”运算得到的向量 V满足 H ( V)≥ tX,其中,H( V)表示V的汉明重量。
2) 安全性条件:对于禁止子集 X ={i1, i2, … ,if}∈ ΓForb,设 D0(D1)为 B0(B1)的 i1, i2,… ,if行构成的子矩阵,则D0=D1。
定义 2 设一个视觉密码方案的原图像为 S,经过秘密分享算法后得到共享份集合T,直接叠加授权子集的共享份,得到恢复图像 S '。若存在一个函数R,满足 S = R ( S'),则称该视觉密码方案是无损分享的。
定理1 满足定义1的视觉密码方案是无损分享的。
证明 通过计算恢复图像 S '中 m个子像素的汉明重量并分类,可以实现原图像S的完全恢复。设原图像S的大小为a×b,S( i, j)对应恢复图像中S'( m i-m + 1 ,j )到S'( mi, j)的 m 个像素,设表示 S '中 m个像素的汉明重量表示像素块的平均汉明重量, W0表示原白像素对应像素块的汉明重量,W1表示原黑像素对应像素块的汉明重量,由定义1可知因此S( x, y)=即存在函数R满足 S = R ( S'),定理1证毕。
实际上对于一个已知基矩阵的方案而言,函数R更容易设计。例如对(2, 2)方案而言,其基矩阵为叠加 2个共享份 T和
1T2得到 S '。S '中的'01'汉明重量为1,对应S的'0';S'中的'11'汉明重量为 2,对应 S的'1'。令(i和 j表示 S的像素坐标),即可完全恢复出原图像。
由定理1的证明和(2, 2)方案的示例可知,无损分享的视觉密码方案在完全恢复原图像时,需要进行abm次加法和ab次取整,其计算复杂度与传统的直接叠加相同,均为 O (1 )。因此无损分享视觉密码既继承了恢复简单的特点,又可以实现完全恢复,待解决的问题是如何减小像素扩展度。
定理2(判别定理) 设 ( ΓQual, ΓForb)为通用存取结构,若m 证明 若以 m为像素扩展度的方案是无损分享的,则m0不是无损分享方案的最小像素扩展度,与已知条件矛盾,定理2证毕。 推论1 对于像素扩展度为1的视觉密码方案而言,若恢复操作为或运算,则该方案是有损分享的。 证明 对于恢复操作为或运算的视觉密码而言,(2, 2)方案的m0最小,且m0=2。因此对所有视觉密码方案均有 m0>1。根据定理 2,若 m=1,则m 由此可见,无损分享视觉密码是一类重要的方案,而且m0是衡量秘密信息能否完全恢复的关键。 一般而言,直接计算m0难度较大,而m0表示的是基矩阵的列数,所以可以将复杂的基矩阵设计问题简化为概率矩阵的最大公约数问题。根据像素扩展度m与最大公约数d的数学关系,建立以d最大化为目标、安全性和对比性为约束条件的整数规划模型,然后利用基矩阵与概率矩阵之间的转化算法,得到最优的像素扩展度及相应的基矩阵。本文设计的优化算法流程如图1所示。 加密规则矩阵和概率矩阵是Hsu等[9]为了避开基矩阵而提出的概念。 定义 3 记 E = [eij]为加密规则矩阵, i ∈{1,2,…,2n},j∈ {1,2,…,n},eij∈ { 0,1}。E中各行向量均不相同,行向量 ei= ( ei1, ei2,… ,ein)表示第i种加密规则,即原图像的1个像素按照 ei加密,生成第j共享份中对应的像素为eij。 定义4 记 C = [cij]为概率矩阵,i ∈ { 0,1}, j ∈{1,2,… ,2n},c ∈ [ 0,1]。其中, c 表示白像素选择第j ij0j条加密规则的概率,c1j表示黑像素选择第j条加密规则的概率,且 生成共享份时,根据概率矩阵选择加密规则。根据表1可知,当原像素为0(白像素)时,以c01=0.5的概率选择e1=(e11, e12),以c04=0.5的概率选择e4=(e41, e42),而e2和e3则不选择;当原像素为1(黑像素)时,以c02=0.5的概率选择e2=(e21, e22),以c03=0.5的概率选择e3=(e31, e32),而e1和e4则不在选择之列。通过上述步骤生成的共享份,其大小与原秘密图像相等,故像素扩展度为1。在衡量方案安全性和对比性时,则根据一个像素为黑色的概率来判断。 在安全性方面,禁止子集{1}和{2}无法得到原图像的信息。T1中原白像素的加密效果为 F C01=,原黑像素的加密效果为 F C =11由于 F C = F C,因此从 T中无 图1 优化算法流程 表1 基于加密规则矩阵和概率矩阵的(2, 2)门限视觉密码 01111法分辨出原图像的像素颜色。对T2的分析同理。 在对比性方面,需要确定授权子集{1,2}能够恢复出原图像。对T1+T2而言,原白像素对应的恢复效果为,原黑像素对应的恢复效果为,由于QC11>QC01,因此从T1+T2中可以分辨出原图像的像素颜色。 为了便于描述m与d之间的数学关系,本节首先介绍矩阵转化算法。 定义5 记能被概率矩阵C中所有元素整除的有理数组成集合D,若d是D中的最大值,则称d为C的最大公约数。 注:由于概率矩阵 C中的元素为[0, 1]的有理数,因此本文是在有理数范围内讨论最大公约数,与通常的自然数范围不同。 矩阵转化算法以加密规则矩阵E和概率矩阵C为算法输入,以基矩阵B0和B1为算法输出,具体步骤如下。 step1 找到C的最大公约数d。 step2 计算修正后的概率矩阵 ' d=C C 。 step3 将加密规则 ei(1 ≤ i ≤ 2n)的转置重复次,并依次连接组成新的矩阵B0。 step4 将加密规则ei(1 ≤ i≤ 2n)的转置重复次,并依次连接组成新的矩阵B1。 由矩阵转化算法可知,若 ( E1, C1) ≠ (E2, C2),则得到的基矩阵是不同的。由于根据基矩阵 B0和B1也可以计算出相应的E和C,因此可以设计以基矩阵为算法输出,以E和C为算法输出的逆算法,具体步骤如下。 step1 根据参与者人数n确定加密规则矩阵E。 step2 统计 B0中加密规则 ei(1 ≤ i ≤ 2n)出现的次数 c0'i。 step3 统计 B1中加密规则 ei(1 ≤ i ≤ 2n)出现的次数 c1'i。 step4 计算概率矩阵 C = C ' m。 定理 3 对一个视觉密码方案而言,其基矩阵的像素扩展度 m与概率矩阵的最大公约数 d满足m = 1 d。 证明 从矩阵转换算法及其逆算法可知,C ' = C d且 C = C ' m,故定理3得证。 下面以(3, 3)门限方案为例,对矩阵转化算法进行说明。加密规则矩阵,概率矩阵则C的最大公约数 d = 1 4,修正后的概率矩阵 C '=。将e的转置重复次,i并依次连接组成新的矩阵将ei的转置重复 c1'i次,并依次连接组成新的矩阵,基矩阵的像素扩展度 m = 4 。 设 Γ=(ΓQual, ΓForb),且对于以Γ为存取结构的视觉密码方案,其最优像素扩展度是以下整数规划模型的解。 1) 规划目标 由于像素扩展度 m = 1 d,因此求m的最小值等价于d的最大值。在视觉密码方案设计过程中,d只随概率矩阵C的变化而取不同的值,因此本模型的规划目标是寻找到一个d最大的概率矩阵C。 2) 对比性约束条件 设 Q C0h( Q C1h)表示授权子集 Qh∈ΓQual(h∈{1,2,…,q})的所有共享份叠加后,原白(黑)像素呈现黑像素的概率。定义 O R ( E , X)(X = { x1, x2,… ,x } ∈ 2p)表示加密规则矩阵E中第 x, x ,… ,x列在 t12t或运算后得到的列向量,则 ( Q C0h, Q C1h)T=C×OR ( E , Qh)。对比性约束条件指授权子集能够恢复秘密图像,故 Q C1h- Q C0h>0。 3) 安全性约束条件 设 F C0k(F C1k)表示禁止子集 Fk∈ΓForb(k∈{1,2,…,f})的所有共享份叠加后,原白(黑)像素呈现黑像素的概率,则 ( F C0k, F C1k)T=C×OR ( E,Fk)。安全性条件表示禁止子集无法获取秘密图像的任何信息,故 F C1k- F C0k= 0 。 4) 其他约束条件 由于d是概率矩阵C的最大公约数,因此 cij=nijd且n∈N(i∈ { 0,1},j∈ { 1,2,… ,2n})。另外由根据概率 ij矩阵的定义,可知和 cij∈ [ 0,1]。 本文设计的像素扩展度优化算法适用于通用存取结构,下面从门限结构和通用存取结构2个方面进行实验与分析,以说明本文算法的有效性。 1) 门限结构 按照像素扩展度的优化算法,计算(k,n)(2 ≤ k ≤ n ≤ 1 0)门限结构视觉密码方案的最优像素扩展度,如表2所示。从计算结果可以看出:对于(n, n)门限结构,表2的结果与文献[1]相同;对于(2, n)门限结构,表2的结果与文献[2]相同;对于(k, n)(2 < k < n ≤ 1 0)门限结构,表2的结果与文献[3]相同。因此本文提出的优化算法对于(k, n)门限结构是有效的。 表2 (k, n)门限结构方案的像素扩展度 2) 通用存取结构 设 P = { 1,2,3,4}, ΓQual= { {1,2},{2,3}, {1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}}, ΓForb={{1,3},{1,4},{2,4},{3,4},{1},{2},{3},{4}},则 ( ΓQual, ΓForb)是通用存取结构。根据文献[4]的累积矩阵方法,计算得到的基矩阵为根据本文方法,计算的基矩阵为m=4,比文献[4]的方法更优,因此本文方法对于通用存取结构是有效的。本方案对应的原图像、共享份和恢复图像如图2所示。 图2 本文方案的实验效果 从图2分析可知,直接叠加共享份得到的 S '能够完全恢复出原图像 S。需要说明的是,对于不同的授权子集,函数R是不同的。比如对于{1, 2},,则 最后从通用存取结构、像素扩展度、相对差、信息损失和恢复计算复杂度等5个方面将本文方案与前人方案进行对比,具体结果如表3所示。其中,m0≤m1, m2,0< Q C1h- Q C0h< 1 。分析表3可知:本文方案在保证原图像完全恢复的情况下,能够有效减小像素扩展度,且不增加恢复过程的计算复杂度。 表3 方案综合比较 在研究秘密图像恢复质量的基础上,本文给出了无损分享视觉密码的定义,保持了恢复简单优点,同时实现了原图像的完全恢复。针对无损分享方案中的像素扩展问题,将像素扩展度 m0的求解问题转化为计算概率矩阵的最大公约数 d,进而设计了像素扩展度的优化算法,包括整数规划模型和矩阵转化算法2部分。本文取得的计算结果只考虑了或运算的情况,对于其他的算子如 XOR等,尚有待进一步的研究。 [1] NAOR M, SHAMIR A. Visual cryptography[A]. Cryptology-Eurocrypt’94[C]. 1994. 1-12. [2] BLUDNO C, SANTIS A D, STINSON D R, et al. Graph decomposition and secret sharing schemes[J]. Journal of Cryptology, 1995, (8):39-64. [3] DROSTE S. New results on visual cryptography[A]. Cryptography-CRYPTO’ 96[C]. 1996. 401-415. [4] ATENIESE G, CARLO B, SANTIS A D, et al. Visual cryptography for general access structures[J]. Information and Computation, 1996, (12):86-106. [5] HAJIABOLHASSAN H, CHERAGHI A. Bounds for visual cryptography schemes[J]. Discrete Applied Mathematics, 2010, (158): 659-665. [6] YANG C. New visual secret sharing schemes using probabilistic method[J]. Pattern Recognition Letters, 2004, (25):481-494. [7] 白璟霖. 以随机乱数为基础的影像机密分享[D]. 铭传大学, 2005.BAI J L. Image Secret Sharing based Upon Random Numbers[D].Ming Chuan University, 2005. [8] HOU Y C, TU S F. A visual cryptographic technique for chromatic images using multi-pixel encoding method[J].Journal of Research and Practice in Information Technology, 2005, 37(2):179-191. [9] HSU C S, TU S F, HOU Y C. An optimization model for visual cryptography schemes with unexpanded shares[A]. ISMIS[C]. Springer-Verlag Berlin Heidelberg, 2006. 58-67.3 像素扩展度的优化算法
3.1 加密规则矩阵和概率矩阵


3.2 矩阵转化算法
3.3 整数规划模型
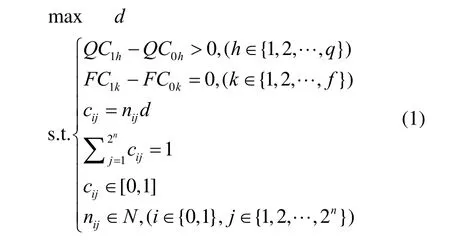
4 实验结果与分析



5 结束语

