证明q-恒等式的一种迭代法
庄世嘉,郑德印
(杭州师范大学理学院,浙江 杭州 310036)
证明q-恒等式的一种迭代法
庄世嘉,郑德印
(杭州师范大学理学院,浙江 杭州 310036)
考虑求和项含有q-二项式系数的一类终止型q-级数恒等式.利用q-二项式系数的两个递推关系,建立了此种q-级数的两个递推关系.作为应用,使用这两个递推关系证明了一些重要而基本的求和公式,例如q-Chu -Vandermond、q-Pfaff-Saalschütz和q-Dixon求和公式.这一迭代法对证明q-级数恒等式是简单和有效的方法.
q-恒等式;q-级数;q-二项式系数;迭代法
0 引 言
众所周知,q-恒等式的证明方法很多,比如迭代法[1-3]、Carlitz反演法[3-4]、q-Lagrang反演法[5]、q-差分法[1 -2]、Abel方法[6]、WZ方法[7]和组合意义证明法[8]等.受文献[9]的启发,本文给出证明q-恒等式的一种迭代法,即通过建立q-组合和的递推公式来证明q-恒等式.从证明过程可以看出,这一方法是证明q-组合和恒等式的一个简单而统一的方法.为了展示这一方法的有效性,在第2节和第3节分别给出了一些重要而经典的q-恒等式和q-级数求和公式的证明过程.在开始这一过程之前,先介绍一些记号、概念和结论.
定义x的n次q-平移阶乘(x;q)n为
(x;q)0:=1, (x;q)n:=(1-x)(1-xq)…(1-xqn-1),n=1,2,….
为了简便,记(a,b,…,c;q)n:=(a;q)n(b;q)n…(c;q)n.定义q-二项式系数为

容易验证,q-二项式系数满足Pascal三角递推关系[2,I.45]:
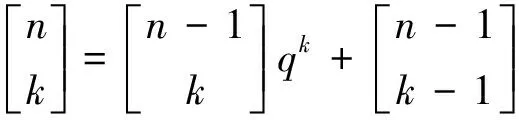
(1)

(2)
基本超几何级数(或q-级数)[1-2]定义为

1 q -组合和的两个递推公式
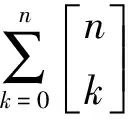
定理1对于正整数n和任意序列α0,α1,…,αn,有递推关系:

(3)
证明当n=1时,结论显然成立.下设n>1,由q-二项式系数的递推关系(1),有


□
定理2对于正整数n和任意序列α0,α1,…,αn,有递推关系:
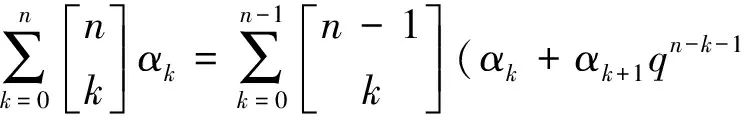
(4)
证明当n=1时,结论显然成立.下设n>1,由q-二项式系数的递推关系(2),有


□
2 基本的q -恒等式
定理3(Goldman-Rota的q-二项式定理[10])对正整数n和任意变量x,y,z,有

(5)
其中,Pn(x,y)=(x-y)(x-qy)…(x-qn-1y).
证明在递推关系式(3)中,令αk:=Pk(x,z)Pn-k(z,y),则有


使用此递推公式,连续迭代n次,得
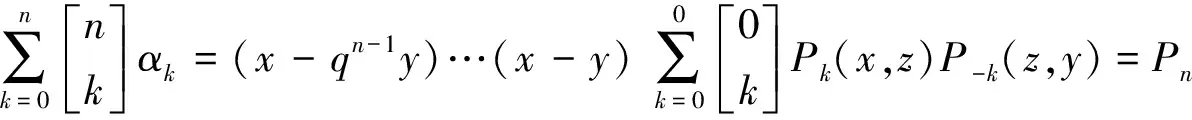
□
注若在式(5)中,取y=0,z=1,则得著名公式
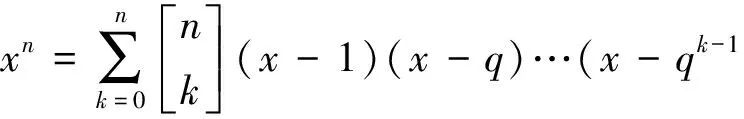
(6)
若在式(5)中,令x=1,z=0,再将y换成z,求和指标k换为n-k,则有
推论4(q-二项式定理[1,P.490,Corollary10.2.2(c)])对正整数n和任意的变量z,有

(7)
若在式(5)中,令x=1,y=ab,z=a,则得
推论5([2,P.25,Ex.1.3])对于正整数n和任意的变量a和b,有

(8)
进一步地,将上等式中的a、b互换,k→n-k,则得等式(8)的另一形式:

(9)
定理6([2,P.33,Ex.1.35])设x和y是具有q交换因子(即xy=qyx)的两个未知量,且满足分配律,那么有
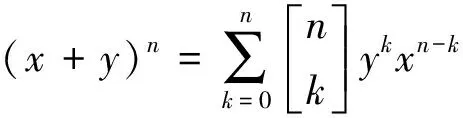
(10)
证明因为xy=qyx,所以xn-k-1y=yxn-k-1qn-k-1.若令αk:=ykxn-k,则
αk+αk+1qn-k-1=ykxn-k+yk+1xn-k-1qn-k-1=ykxn-k-1x+ykxn-k-1y=ykxn-k-1(x+y).
于是由递推关系(4),有

□
注等式(10)形式上非常类似于二项式定理,但实际上是完全不同的.此等式也揭示了q-二项式系数是如何产生的.另外,本节中的恒等式都是重要而经典的q-恒等式,有很多其他的证明方法,如数学归纳法、迭代法、待定系数法和q-差分法等等,见文献[1-3].
3 q -级数求和公式
定理7(q-Chu-Vandermonde公式[2,II.6,II.7])对任意正整数n和复参数b、c,有

(11a)

(11b)
证明若将公式(11a)中的和翻转,即将求和指标k换成n-k,然后参数b、c分别换成q1-n/c、q1-n/b,那么(11a)变成(11b).所以这里仅证(11a).首先将(11a)改写为
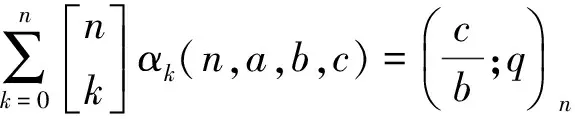
(12)

αk(n,a,b,c)qk+αk+1(n,a,b,c)=(1-c/b)αk(n-1,a,b,cq).
将这一结果代入到递推公式(3)中,则有

连续迭代此递推公式n次,得
Ωn(a,b,c)=(1,c/b)Ωn-1(a,b,cq)=(1-c/b)(1-cq/b)Ωn-2(a,b,cq2)=
…=(1-c/b)(1-cq/b)…(1-cqn-1/b)Ω0(a,b,cqn).
因Ω0(a,b,cqn)=1,则等式(12)得证.
□
定理8(q-Pfaff-Saalschütz求和公式[2,II.12])对任意正整数n和复参数a、b、c,有

(13)
证明将等式(13)右边的分母乘到左边,化简整理,则要证等式可改写为

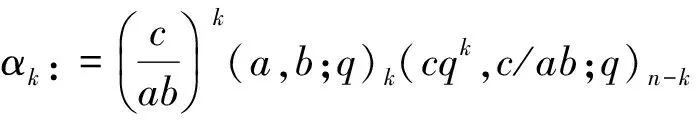
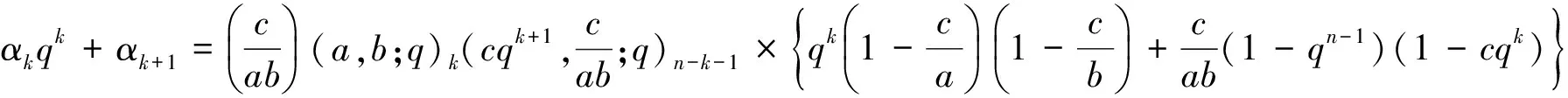

由这两个结果,然后{(3)-(c/ab)×(4)}/(1-c/ab),得
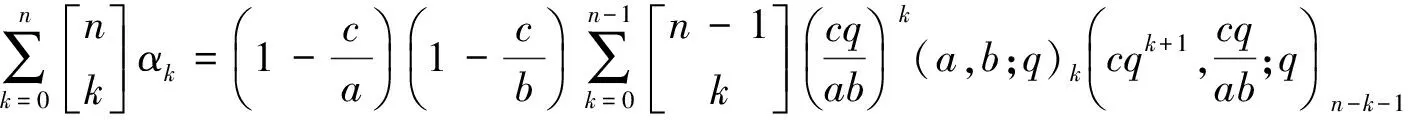
若记上等式左端为Ωn(a,b,c),那么上等式可改写成
Ωn(a,b,c)=(1-c/a)(1-c/b)Ωn-1(a,b,cq).
连续迭代此递推关系n次,有

由Ω0(a,b,cqn)=1,证得式(13).
□
注等式(13)左边级数的特点是q与分子参数之积等于分母参数之积,这是q-级数的一种重要类型,称为Saalschütz型的.公式(3)是Pfaff-Saalschütz公式[2]
的q-模拟,1910年由Jackson[11]导出,其证明方法一般是利用q-二项式定理[1]、Heine变换[3]和级数重排的方法[11],文献[8]从整数分拆的角度给出了一个组合证明.这里给出的方法是q-组合和迭代法,无需借助于其他的定理,证明过程非常简单.
定理9(终止型q-Dixon求和公式[2,II.21])对任意正整数n和复参数a、b、c,有

(14)
证明将等式(14)右边的分母乘到左边,约掉等式两边的因子(aq;q)n,则式(14)可改写为

(15)


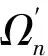
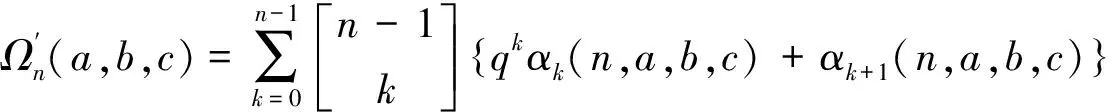
而


上面大括号中的式子可以重新组合、因式分解为


这样,qkαk(n,a,b,c)+αk+1(n,a,b,c)可改写为
(1-aq/bc)(1-aq1+2k)αk(n-1,aq,b,c)+aq2kαk(n,a,b,c)+aq1+k+nαk+1(n,a,b,c).
所以
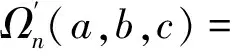

对最后一个和式作指标代换:k→k-1,然后用公式(2)将其与第二个和合并,则有

因此
Ωn(a,b,c)=(1-aq/bc)Ωn-1(aq,b,c).
连续迭代此递推公式n次,并注意到Ω0(aqn,b,c)=1,得
Ωn(a,b,c)=(1-aq/bc)Ωn-1(aq,b,c)=(1-aq/bc)(1-aq2/bc)Ωn-2(aq2,b,c)=
…=(aq/bc;q)nΩ0(aqn,b,c)=(aq/bc;q)n.
定理9证毕.
□

[1] Andrews G E, Askey R, Roy R.Special functions[M].Cambridge: Cambridge University Press,2000:481-526.
[2] Gasper G, Rahman M.Basic hypergeometric series[M].2nd Edition.Cambridge: Cambridge University Press,2004:4-76.
[3] 初文昌,王晓霞.基本超几何级数:恒等式快速入门[J].数学研究与评论,2008,28(2):223-250.
[4] Chu Wenchang.Inversion techniques and combinatorial identities: basic hypergeometric identities[J].Publicationes Mathematicae Debrecen,1994,44:301-320.
[5] Gessel I, Stanton D.Applications ofq-lagrange inversion to basic hypergeometric series[J].Transactions of the American Mathematical Society,1983,277(1):173-201.
[6] Chu Wenchang, Jia Cangzhi. Abel’s method on summation by parts and terminating well-poisedq-series identities[J]. Journal of Computational and Applied Mathematics,2007,207(2):360-370.
[7] Gessel I M.Finding identities with the WZ method[J].Journal of Symbolic Computation,1995,20(5/6):537-566.
[8] Goulden I P. A bijective proof of theq-Saalschütz theorem[J]. Discrete Math,1985,57:39-44.
[9] González L. A new approach for proving or generating combinatorial identities[J].International Journal of Mathematical Education in Science and Technology,2010,41(3):359-372.
[10] Goldman J, Rota G C.On the foundations of combinatorial theory. IV. Finite vector spaces and eulerian generating functions[J]. Studies in Applied Mathematics,1970,49:239-258.
[11] Jackson F H .Transformations ofq-series[J]. Mess Math,1910,39:145-153.
AnIterativeMethodforProvingq-identities
ZHUANG Shijia, ZHENG Deyin
(College of Science, Hangzhou Normal University, Hangzhou 310036, China)
The paper discussed a kind of terminatingq-series identities whose summation contains theq-binomial coefficient, established two recursive relations of suchq-series with two recursive relations of theq-binomial coefficient, and used these two recursive relations to prove some basic and important summation formulas such as theq-Chu-Vandermond,q-Pfaff-Saalschütz andq-Dixon sum formula. This iterative method is a simple and useful approach for provingq-series identities.
q-identities;q-series;q-binomial coefficient; iterative method
2013-01-20
浙江省自然科学基金项目(LY12A01030).
郑德印(1964—), 男, 副教授, 主要从事组合数学、超几何级数和特殊函数研究. E-mail:deyinzheng@hznu.edu.cn
10.3969/j.issn.1674-232X.2013.04.010
O157.1MSC201011B65; 33D15
A
1674-232X(2013)04-0332-06

