无粘结预应力RPC简支梁受弯性能分析

付 强, 罗丽娜, 邓 宁，祁凯能，金凌志

无粘结预应力RPC简支梁受弯性能分析

付 强1,*罗丽娜1, 邓 宁2，祁凯能1，金凌志1

（1. 广西岩土力学与工程重点实验室桂林理工大学，广西，桂林 541004; 2. 广西建筑科学研究设计院，广西，南宁 530011）

活性粉末混凝土是一种新型超高性能混凝土材料，为了详细评估非预应力筋配筋率、预应力筋配筋率、混凝土强度、非预应力筋屈服强度等对预应力混凝土梁的受弯性能的影响，建立了上述各种参数影响下的无粘结预应力RPC简支梁的有限元模型。通过对比分析研究得出随着非预应力筋配筋率和无粘结预应力钢绞线配筋率的提高，跨中极限弯矩增大，跨中极限挠度和钢绞线应力增量降低；随着非预应力筋的屈服强度、混凝土轴心抗压强度的提高，跨中极限弯矩和挠度也缓慢增大，力筋应力增量相应增加。为实际工程预应力RPC结构的优化设计提供参考数据。

无粘结预应力；活性粉末混凝土；受弯性能；参数分析

0 引言

预应力活性粉末混凝土（简称RPC）是一种超高性能的水泥基复合材料[1]，其强度高、耐久性好、韧性及体积稳定性良好等特点，受到了国内外学者的广泛关注，并进行了大量的试验研究。1993年法国Richard[2]等人研制出活性粉末混凝土；湖南大学何峰，黄政宇[3]等人在不同养护条件下制成114~215 MPa的混凝土；闫光杰[4]通过试验建立了RPC的本构关系及破坏准则；郑文忠[5]等人通过6根简直梁试验建立了RPC梁的正截面受弯承载力、刚度、裂缝的计算方法；王文雷[6]采用有限元模拟，得出配筋率对RPC预应力梁承载力的影响关系。总之，影响预应力活性粉末混凝土构件承载力的因素很多，主要有预应力筋配筋率、非预应力筋配筋率、混凝土强度、非预应力筋屈服强度等，无粘结预应力混凝土梁的力学性能较为复杂，一般的力学理论难以反映其特性，而试验需耗费大量的资源。因此，采用有限元模拟分析不失为一种适宜的方式，通过计算可以获得大量数据，以找出普遍性的规律，同时可弥补试验的局限性和不足。本文通过建立有限元模型对影响预应力RPC梁受弯性能的重要参数进行了较为系统的对比研究。

1 试验概况

1.1 试件配比

表1 混凝土配合比

注：采用直径约为0.2 mm和长度约为13 mm的镀铜光面平直钢纤维，其抗拉强度大于2000 MPa。

1.2 材性试验分析

通过对RPC的材性试验，得到RPC力学性能如表2。

表2 RPC力学性能指标

1.3 试验梁的制作及养护

本次试验共设计4种（8根）活性粉末混凝土无粘结预应力简支梁（图1），梁长L=2000 mm，计算跨度l=1800 mm，截面b×h=120 mm×150 mm矩形梁，预应力筋线型为直线型，详见图1和表3。构件浇筑完成24 h后即可拆模，拆模后对构件撒水养护，在常温下养护28 d。

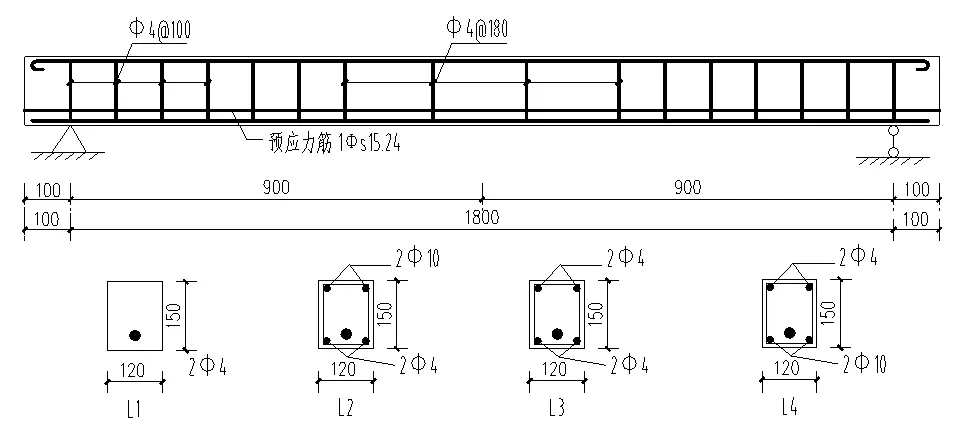
图1 试验梁的截面尺寸及配筋图

表3 无粘结预应力混凝土试件设计表

2 预应力RPC简支梁的数值模拟

2.1 有限元模型建立

在无粘结预应力活性粉末混凝土梁的有限元模型建立过程中，采用体分割法工作量比较大，为简化建模，采用独立耦合法比较适合。此方法是将模型中的混凝土和预应力钢筋分别建模并且划分成网格，然后只将混凝土与预应力筋在梁截面方向上的自由度耦合，使得预应力筋在梁的纵向方向可以自由的滑动，以模拟混凝土和预应力筋之间无粘结的特性。在梁的两端将混凝土的节点与预应力筋两端的节点完全耦合，使混凝土和预应力筋在三个方向都保持相同的滑动方向，以模拟预应力筋与梁的锚固。本文不做抗剪研究的分析，因此没有设置抗剪箍筋，图2为配置钢筋骨架图，图3为有限元的模型图。

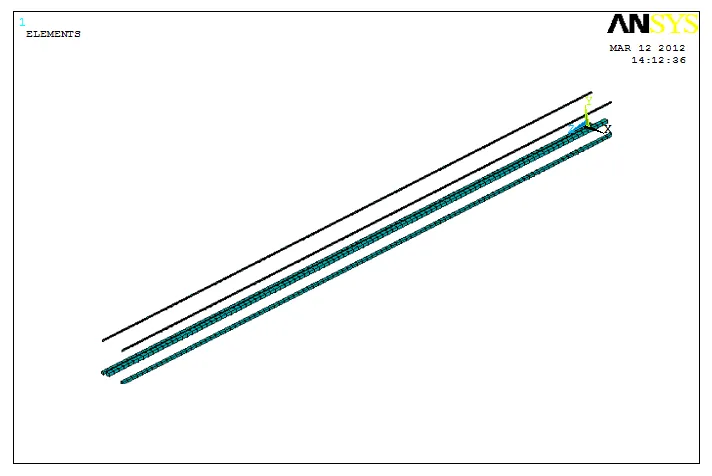
图2 配置钢筋骨架图

图3 有限元模型图

2.2 有限元法的求解设置和算法

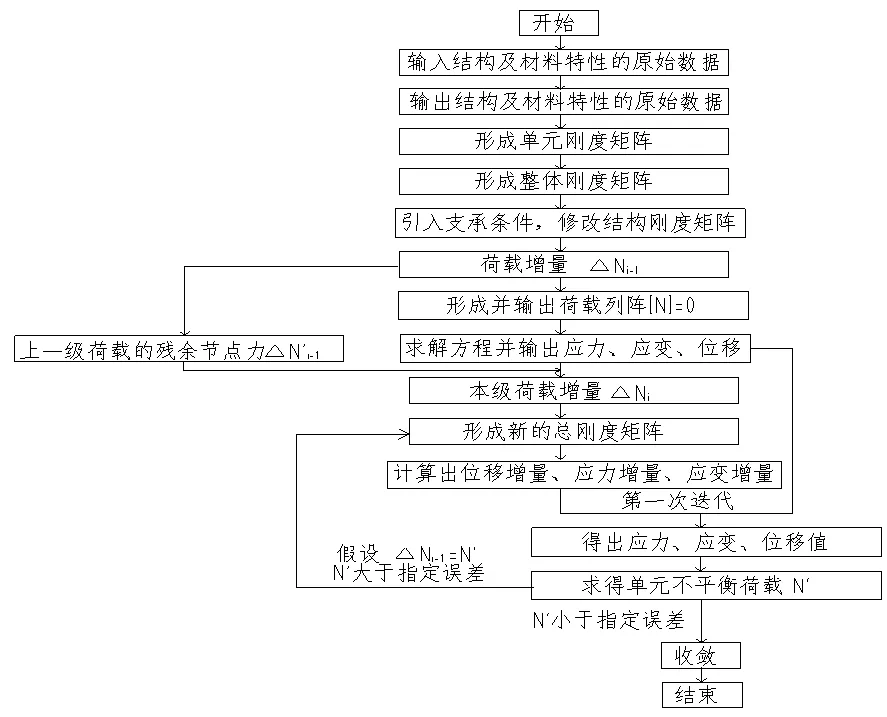
图4 非线性方程的求解过程

2.3 有限元计算结果与试验结果对比

根据前面所采用的参数，建立RPC梁模型，进行对比分析如下：

（1）预应力筋张拉阶段对比对预应力筋单元，采用降温法对其施加张拉力来模拟预应力筋的张拉过程，张拉后的混凝土应力云图如图5。

试件在预应力作用下产生反拱，张拉过程中各级反拱值通过百分表测量测得。图6为每级张拉力－反拱的曲线图，可以看出，L1-L4试验梁的张拉力－反拱曲线很相似，在初始阶段都有一些弯曲，使反拱值不稳定；当张拉力达到一定值后，曲线呈现明显线性增长，说明在预拉区的混凝土还没有出现裂缝，构件还处于弹性工作状态；对比ANSYS计算值发现，L1梁试验值与计算值相差较大，计算值比试验值大26.6%，L2~L4梁试验值与ANSYS计算值都呈一条斜率基本稳定的直线，两者之间的吻合度较高；再比较4种不同配筋梁的反拱值，L1梁无非预应力筋，L2梁底部为2根Φ10，L3、L4底部为2根Φ4，随着底部非预应力钢筋配筋率的提高，反拱值降低。

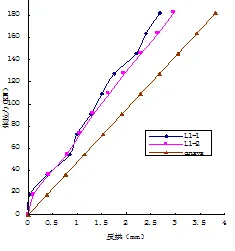
图8为各梁的荷载－挠度曲线图，试验值与ANSYS计算值的发展趋势一致，挠度变化曲线历经三个阶段。第一阶段：出现裂缝之前，试件处于弹性工作阶段，曲线趋于直线，试验值曲线斜率比计算值的小，主要是试验值的刚度低于计算值；第二阶段：混凝土随着荷载增大出现了裂缝而退出工作，曲线斜率逐渐降低，受拉区力转为由纵筋来承担，从而导致了梁的刚度下降，该阶段试验值与计算值曲线斜率较为吻合；第三阶段：随着荷进一步增大，纵筋屈服进入塑性阶段，此时预应力筋承担所有力，曲线斜率逐渐降低，而该阶段试验值与计算值料吻合。

（2）加载阶段的对比

模拟三分点加载直至试验梁破坏的过程，加载后挠度及混凝土应力云图如图7所示。

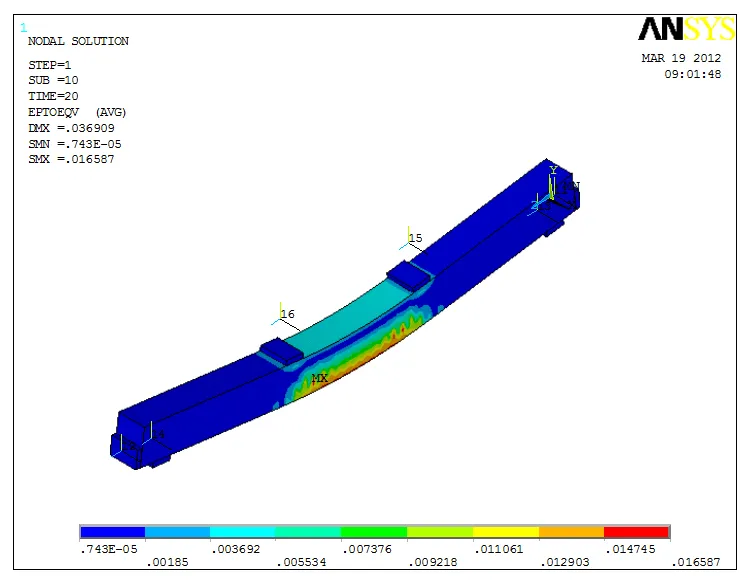
3 不同参数设置对模型的影响分析

计算模型中用于评估而改变的主要参数有：1)非预应力筋配筋率ρ；2)预应力筋配筋率ρ；3)非预应力筋屈服强度f；4)混凝土强度f。共设置了四个系列的无粘结预应力RPC简支梁，详见见表4。

表4 用于不同参数分析的各种预应力RPC混凝土简支梁汇总表

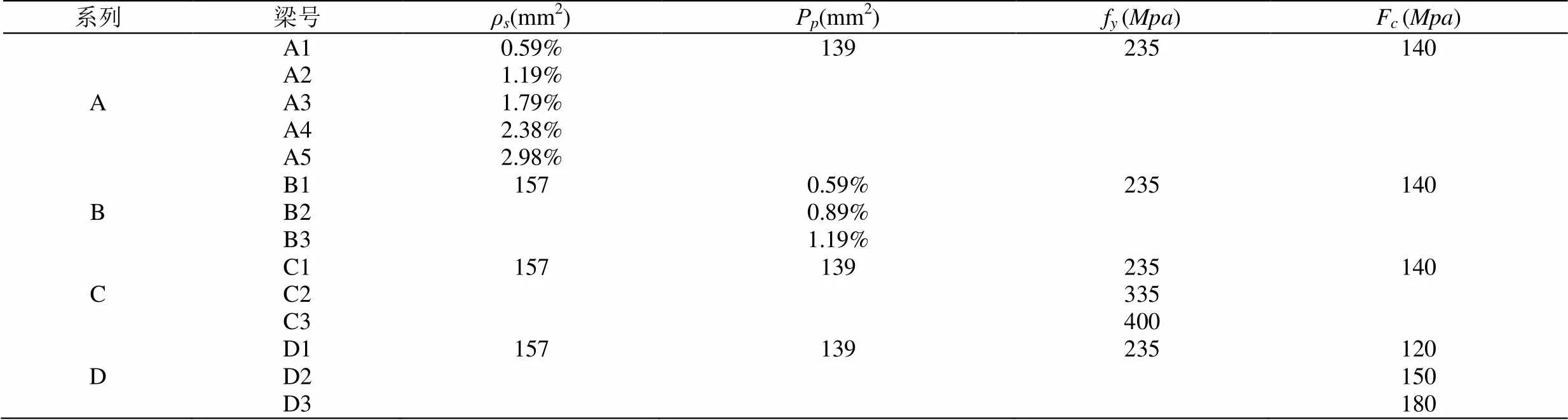
Table4 The various prestressed concrete RPC the Charpy summary table for different parameter analysis

3.1 非预应力筋配筋率的影响

以受拉区纵向非预应力钢筋配筋率为变量，配筋率ρ范围为0.59%~2.98%。

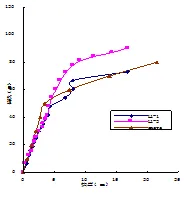
表5为对应于非预应力筋配筋率ρRPC梁的计算结果。图9和图10给出了不同ρ预应力RPC梁的荷载－挠度和荷载－应力增量曲线。

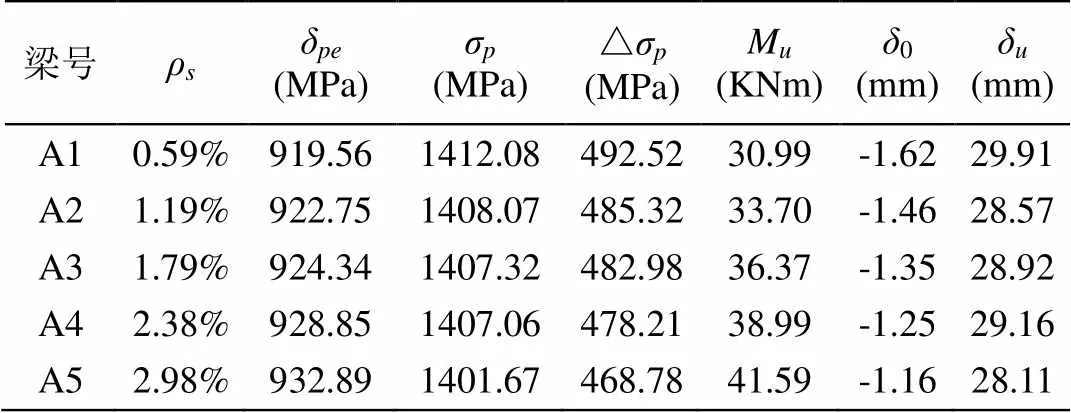
表5 非预应力筋配筋率ρs对梁计算的结果

图表结果显示，随着配筋率ρ增大，钢筋进入塑性阶段的时间也延长，在同一荷载作用下，ρ越小，梁的挠度越大。受拉区纵向非预应力钢筋配筋率从0.59%增加到2.98%，极限弯矩则从30.99 KN.m增加到41.59 KN.m，增加了34.2%；梁的反拱值由-1.62 mm下降到-1.16 mm，下降了27.96%；跨中极限挠度从29.91 mm减小到28.11 mm，减小了6.03%；非预应力钢筋配筋率ρ从0.59%增加至2.98%，预应力筋的应力增量△σ从492.52 MPa降低到468.78 MPa，降低率为4.82%，说明无粘结预应力的应力增量随着配筋率的增加而降低。

3.2 预应力筋配筋率ρp的影响

表6 预应力筋配筋率ρp对梁计算的结果

图表结果显示，在同一荷载作用下，ρ越小，梁的挠度越大。随着预应力筋配筋率ρ的增加，梁破坏时，极限承载力提高，梁跨中挠度降低，预应力筋应力增量减小。当预应力筋配筋率ρ从0.59%增加到1.19%时，极限弯矩从25.25KN.m增加到43.22 KN.m，增加了71.17%；跨中极限挠度从40.26 mm减小到23.47 mm，减小了41.68%；预应力筋应力增量△σ从554.26 MPa降低到了418.65 MPa，降低了24.47%。

3.3 非预应力筋屈服强度fv的影响

以非预应力筋的屈服强度f为变量，变量范围为235 MPa~400 MPa。表7给出非预应力筋屈服强度f对梁计算数据的影响。图13、图14为不同非预应力筋的屈服强度预应力RPC梁的荷载－挠度和荷载－应力增量曲线。

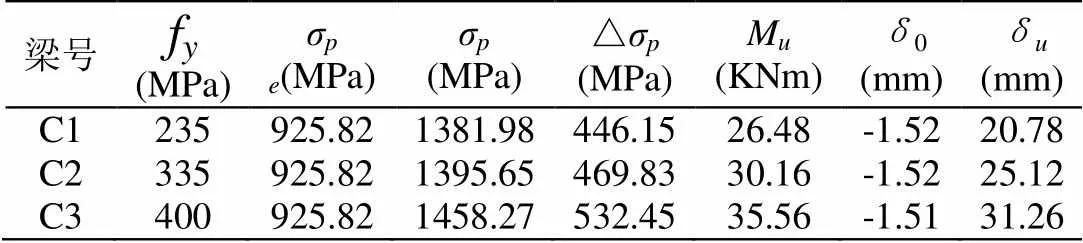
表7 非预应力筋屈服强度fv对梁计算的结果

图表结果显示，跨中极限挠度和极限荷载随着非预应力筋屈服强度f的提高缓慢增大。曲线在第一阶段的变化几乎完全一致，开裂荷载也近似相同，混凝土出现裂缝后曲线开始分离，钢筋进入屈服阶段，非预应力筋屈服强度f较高的梁，其挠度和预应力筋应力增量的变化都稍显缓慢。随着非预应力筋屈服强度的提高，应力增量缓慢增大。当非预应力筋的屈服强度f由235 MPa到400 MPa时，极限弯矩从26.48KN·m增加35.56 KN·m，增加了34.29%；跨中极限挠度从20.78 mm减小到31.26 mm，增加了50.44%；预应力筋应力增量△σ从456.16 MPa增加到了532.45 MPa，增加了16.72%。

3.4 混凝土强度fc的影响

混凝土强度f变量范围为120 MPa~180 MPa，表8为混凝土强度f对梁的计算结果，图15和图16分别给出了不同混凝土强度的跨中弯矩—挠度曲线荷载—应力增量曲线。

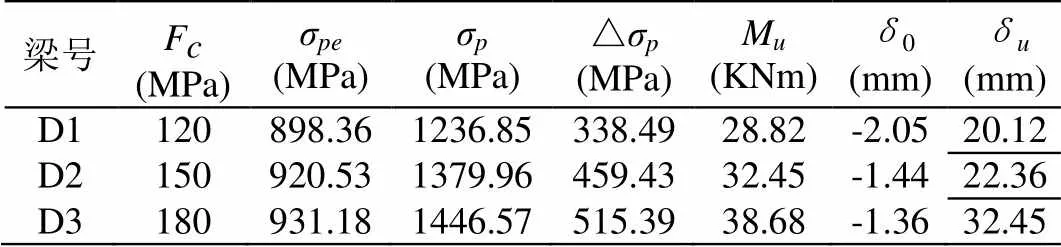
表8 混凝土强度fc对梁计算的结果

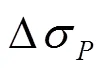
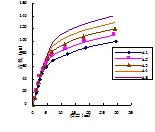
图9 ρs对荷载－挠度曲线的影响

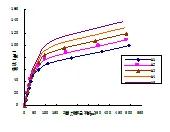
图10ρs对荷载－应力增量曲线的影响

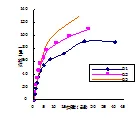
图11 ρn对荷载－挠度曲线图的影响

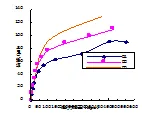
图 12ρs对荷载－应力增量曲线的影响

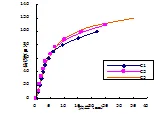
图13 fv对荷载－挠度曲线的影响

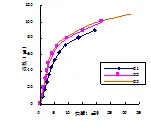
图14 fv对荷载－应力增量曲线的影响

图15 fv对荷载－挠度曲线的影响

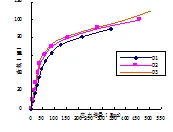
图16 fv对荷载－应力增量曲线的影响

4 结论

(1)有限元程序ANSYS能较好地模拟无粘结预应力RPC简支梁力筋张拉及加载试验过程，可以作为辅助计算工具，为实际工程设计服务；

(2)随着非预应力筋配筋率ρ的提高，梁开裂后的刚度和极限弯矩显著提高，梁的跨中极限挠度和预应力钢筋应力增量降低，但梁的延性随之降低；

(3)随着预应力筋配筋率ρ的提高，预应力筋的初始应力σ增大，梁的反拱值增大；开裂弯矩、梁的刚度显著提高，但梁的延性也随之降低；

(4)随着非预应力筋的屈服强度f的提高，梁的极限弯矩和跨中极限挠度也有缓慢的增大。

(5)随着混凝土轴心抗压强度f的提高，开裂弯矩增大，梁的刚度有所提高，极限弯矩缓慢增加，极限挠度增大，开裂弯矩增大，力筋应力增量相应缓慢增加。

[1] 覃维祖,曹峰. 一种超高强混凝土—活性粉末混凝土[J].工业建筑,1999 (4):72-76.

[2] Richard P, Cheyrezi M.composition of reactive powder concrete[J].cement and concrete research,1995, 25(11): 1501-1511.

[3] 何峰,黄政宇.200-300MPa活性粉末混凝土（RPC）的配制技术研究[J].混凝土与水泥制品,2000(4):44-49.

[4] 闫光杰.200MPa活性粉末混凝土（RPC200）的破坏准则与本构关系[D].北京:北京交通大学,2005.

[5] 郑文忠,李莉,卢珊珊.钢筋活性粉末混凝土简直梁正截面受力性能试验研究[J].建筑结构学报,2011(6):57-60.

[6] 王文雷.RPC预应力梁相关设计参数研究[D].北京:北京交通大学,2006.

[7] 胡成.钢筋混凝土板的非线性有限元分析与计算[J].合肥工业大学学报,1998(12):86-89.

NON-BONDED PRESTRESSED RPC CHARPY FLEXURAL PERFORMANCE ANALYSIS

*FU Qiang1, LUO Li-na1, DENG Ning2, QI Kai-neng1, JIN Ling-zhi1

（1.Guangxi Key Laboratory of Geomechanics and Geotechnical Engineering Guilin University of Technology, Guilin, GuangXi 541004, China;2.Guangxi Institute of Building Research and Design,Nanning,GuangXi 530011, China）

Reactivepowderconcreteisanewultra-high-performanceconcretematerialswith?superiorcharacteristicsoftheultra-high-strength,hightoughness,high?durability. In order to detailed assessment of the prestressed reinforcement ratio, prestressed reinforcement ratio, concrete strength, the yield strength of prestressed steel factors on prestressed concrete beam bending performance influence, we proposed the unbonded prestressed RPC beam finite element model under the influence of the various factors. Through the comparative analysis research concluded. Firstly, with the prestressed reinforcement ratio and unbonded prestressed steel strand reinforcement ratio increase, the middle of span ultimate bending moment is increased slowly. The middle of span limit deflection and steel strand stress is also increased decreased. Secondly, with non-prestressed steel yield strength, concrete axial compressive strength increase, the middle of span ultimate bending moment and deflection is also slowly increases and the stress increment is increased slowly. For practical engineering, prestressed RPC structure optimization design provides reference data.

unbonded prestressed ; reactive powder concrete ; nonlinear analysis ; parametric analysis

TU312.1 TU317.1

A

10.3969/j.issn.1674-8085.2013.03.017

1674-8085(2013)03-0069-07

2013-02-21；

2013-03-18

广西岩土力学与工程重点实验室资助课题（11-cx-04); 广西科技攻关项目(桂科攻0995004)

付 强(1963-)，女，河北阜城人，副教授，主要从事结构工程及加固研究(E-mail: 0331fuqiang@163.com);

*罗丽娜(1988-)，女，广西百色人，硕士生，主要从事结构工程及加固研究(E-mail: 527864278@qq.com);

邓 宁(1962-)，男，广西玉林人，高级工程师，主要从事结构工程及加固研究(E-mail: 1617892368@qq.com);

祁凯能(1986-)，男，湖北武汉人，硕士生，主要从事结构工程及加固研究(E-mail: 89349133@qq.com);

金凌志(1959-)，女，湖南娄底人，教授，主要从事结构工程及加固研究(E-mail: 691023332@qq.com).