我国经济波动与经济增长关系研究——基于ARMA-GARCH-M模型的经验分析

■徐 伟

一、引言

2008年9月16日，美国投行雷曼兄弟申请破产保护，雷曼兄弟成为次贷危机倒下的第一张多米诺骨牌。紧接着，大量次级抵押贷款机构和银行破产，投资基金被迫关闭，股市剧烈震荡引起的金融风暴席卷全球。

从整个人类社会发展历程来看，在工业革命以前，经济增长率基本上围绕0值上下波动;而工业革命后，世界经济发生了巨大的变化，欧美国家的经济开始腾飞，经济总量几乎以几何级数增长。但是，经济运行轨迹并不是一条直线，除了经济增长以外，经济发展的过程中还伴随着起伏不定的经济波动。当出现巨大的经济波动的时候，特别是经济危机的爆发，往往给资本主义社会以沉重的打击。这种经济波动在学术界被称为“经济周期”。

准确说来，经济周期和经济波动这两个概念不能完全等同，经济波动涵盖的范围更广，它不仅包括经济周期变动，还包括经济运行中出现的季节性变动，以及随机性变动，经济波动强调的是经济运行并非平稳运行。本文把经济周期与经济波动二者等同，采用广义的经济波动定义。Jacobs指出:“宏观经济波动的研究并不关注转折点问题，而是试图获取宏观经济时间序列的一般模式，如序列的波动性。”本文中的计量分析阶段采取Jacobs的定义。

自新中国成立以来，我国经济增长就一直处于波动之中，经济运行态势总体呈现出高增长高波动的态势。1953年到2011年间我国经济增长的波动幅度约0.07个标准差，年人均GDP增长率大约为6.91个百分点。由此我们不禁要问，我国经济波动与增长关系如何?回答此问题，对我国宏观经济政策具有重要意义。经济波动对长期经济增长的影响是衡量波动福利效应程度大小的一个重要因素。若能确定两者之间为正相关关系，则消除经济波动有损长期经济增长;若负相关，则消除波动有利于长期经济增长。

理论上关于经济波动与经济增长的关系存在着不同观点。Keynes、Ben Bernanke、Woodford 研究认为，经济波动将导致企业投资风险上升，如果投资者考虑到投资风险，就会减少对投资的需求，这将加大经济的波动，进而扩大投资项目风险，最终由于投资需求不足而降低了产出水平。然而，Turnovsky和Chattopadhyay基于债务约束和资本市场不完善角度构建动态随机一般均衡模型，他们的研究表明，在某些条件下经济波动有利于经济增长。传导机制或传导渠道的差异，导致了经济学家对经济波动与经济增长关系认识的差异，理论观点的差异导致了学者们转向了实证分析。

然而，实证上得出的结论也同样存在分歧。一是负相关。Zarnowitzect研究了美国经济周期波动，其研究结论表明，当经济增长率处于较低水平期间，GNP增长率的标准差倾向于更高;Ramey和Ramey认为，一国的经济波动越高，具有越低的经济增长率;Martin和Rogers研究了欧洲国家和经合组织国家的经验数据，表明经济波动与经济增长之间具有负向相关关系;Kneller和Young使用了1961—1997年经合组织国家的面板数据，得出了二者存在负向相关关系的结论;Fatas基于1950—1998年跨国面板数据进行实证分析，得出经济波动与经济增长之间存在反向相关关系。二是正相关。Roger Kormendi和Philip Meguire的研究发现，更高的产出增长率标准差导致更高的平均增长率水平;Grier和Tullock使用了经济增长率的标准差来表示经济波动，认为产出波动与平均产出增长率之间正相关;Caporale和Mckiernan利用英国1948—1991年的月度数据和美国1971—1993年的年度数据，基于GARCH-M模型的研究得出，产出波动与产出增长正相关。

国内学者利用不同类型的数据序列和计量回归技术，从不同层面对我国经济波动与经济增长之间的关系进行了实证分析。这些研究虽然使用了面板数据，但假设数据生成过程是稳定的，忽略了结构变化的可能性。同时，虽有研究考虑到变量之间的非线性，运用了TGARCH-M模型，但其研究结论不显著。本文基于ARMA-GARCH-M模型，扩充研究样本容量，重新审视了我国经济波动与经济增长的关系。

二、模型设立

金融领域的经验研究表明，很多资产价格变动存在群集波动的现象，也就是说，金融时间序列在一段时间内表现为大幅变动，另一段时间内表现较为平稳。Robert Engle引入了自回归条件异方差(ARCH)模型，来估计经济时间序列的时变条件方差的系数。如果采用OLS估计法得到的结果无序列相关性，但具有显著的ARCH效应，这将导致无偏但非有效的参数估计结果。ARCH模型提供了解决办法，其表示如下:

方程(2)显示了条件方差具有序列相关性。ARCHM模型则将条件方差(ht)引入到均值方程(1)中。自回归条件异方差(ARCH)模型的高阶形式在其方差方程中会包含多阶滞后误差平方项。因为方差非负，要保持误差平方项的平稳性，必须满足(2)式中系数的加权平均为正，这些ARCH模型要通过迭代的非线性最大似然估计法得到。本文使用广义自回归条件异方差(GARCH)模型，该模型只需使用少数几个参数就能拟合大部分时间序列。特别是当均值方程中的残差项存在高阶ARCH效应时，更应该采用GARCH模型，如果采用GARCH(1，1)模型，则上面的ARCH模型中的方差方程改为:

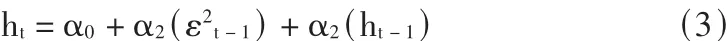
GARCH-M过程是在GARCH模型的均值方程中，加入了条件方差项作为回归元。

三、实证分析

(一)数据

本文采用我国1953—2011年人均国内生产总值增长率数据，数据来源于中经网统计数据库综合年度数据，如图1所示:

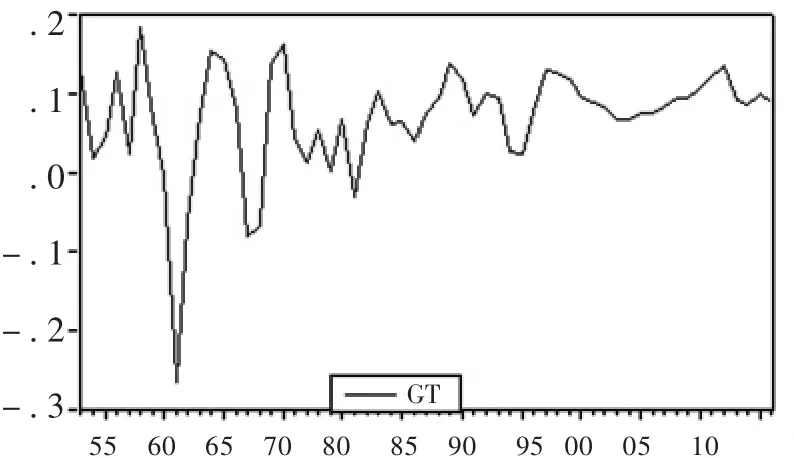
图1 我国1953—2011年人均GDP增长率折线图(%)

上图显示了我国人均GDP增长率的变动情况，在改革开放前，人均GDP增长率波幅较大，改革开放后，人均国内生产总值增长率波动较为平缓。为了对经济增长时间序列进行计量分析，先对该序列做平稳性检验，这里，笔者采用ADF检验方法，检验结果显示增长率指标ADF值为-5.5242，对应P值为0，所以该序列为一平稳时间序列。

(二)ARCH效应检验

我国人均GDP增长率为一平稳时间序列。但是，对其进行白噪声检验后发现，该序列为非白噪声序列。接下来，笔者对人均国内生产总值增增长率时间序列利用Box-Jenkins方法建立ARMA模型，并根据AIC值和SC值确定滞后阶数。其中，ARMA(1，2)过程对该时间序列的拟合情况较好(括号内为t统计量值):

进行GB检验后，发现直到滞后12阶，上述方程的残差都不存在序列相关性。但是，残差存在显著的条件异方差，本文采用ARCH-LM检验法对该序列进ARCH效应检验，检验结果表明，5阶滞后的ARCH-LM检验P值为0.3941，而10阶和15阶的P值为0，故上述ARMA(1，2)模型的残差序列存在GARCH效应。

(三)ARMA—GARCH模型

为了纠正经济增长率数据中存在的条件异方差，笔者将基于GARCH模型并采用极大似然法进行估计，即在方程(4)的基础上加入方差方程:

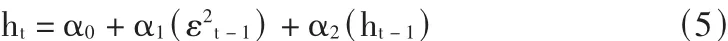
ARMA—GARCH模型估计结果如下 (括号内为z统计量值):

从估计的方程(6)和(7)中ARCH项和GARCH项的参数统计量z值来看，ARCH项和GARCH项系数十分显著。对估计的 ARMA(1，2)— GARCH(1，1)模型进行残差诊断，检验结果显示，滞后1阶F统计值为0.2464，对应P值为0.6216，滞后10阶F统计值为0.6234，对应P值为0.7841，因此接受原假设，可以认为ARMA(1，2)—GARCH(1，1)模型的随机误差项已不存在 ARCH或GARCH效应了，并且ARCH项和GARCH项的系数在1%的置信水平下都十分显著。因此，ARMA(1，2)—GARCH(1，1)模型拟合较好，根据估计的 ARMAGARCH模型，我们可以得到条件方差时间序列，图2给出了我国人均GDP增长率的条件方差序列。

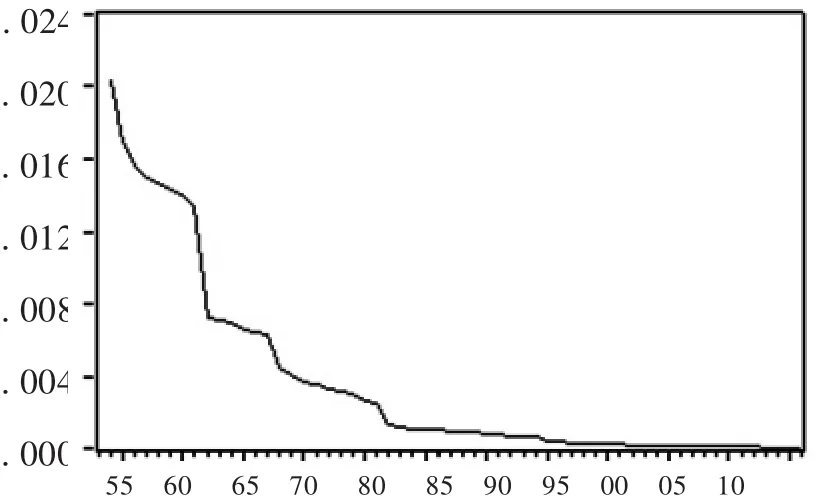
图2 我国GDP增长率的条件方差

笔者把上述条件方差时间序列作为衡量经济波动的指标 (ht)，为了初步考察经济波动与经济增长率之间的关系，先对该经济波动时间序列做平稳性检验，其ADF值为-6.6175，对应P值为0，表明经济波动为一平稳时间序列。

对经济波动时间序列与经济增长率时间序列二者做格兰杰因果关系检验，根据AIC值和SC值，我们选择滞后3期做格兰杰因果检验。对于ht不是Gt的格兰杰原因的原假设，F统计值为3.9762，对应P值是0.0131，在5%的置信水平下，拒绝经济波动不是经济增长的格兰杰原因的原假设;对于Gt不是ht的格兰杰原因的原假设，F统计值为23.2341，对应P值是0，在1%的置信水平下，拒绝经济增长不是经济波动的格兰杰原因的原假设。因此，从统计意义上来讲，在5%的置信水平下，经济波动与经济增长之间互为格兰杰原因。

(四)ARMA— GARCH—M模型

前面的格兰杰因果检验初步认定了经济增长与经济波动之间存在相关关系，而为弄清楚二者之间的正/负向相关关系，我们通过建立ARMA(1，2)—GARCH(1，1)—M模型来检验产出增长率的方差对产出增长率的具体影响，估计结果如下(括号中为z统计量值):

然后，对估计的 ARMA(1，2)—GARCH(1，1)—M 模型进行残差诊断，结果显示，滞后5期F统计值为16.9852，对应P值为0，滞后15期F统计值为3.6449，对应P值为0.0017。因此，可以认为，ARMA(1，2)—GARCH(1，1)—M模型的残差仍存在GARCH效应。为此，我们建立ARMA(1，2)—GARCH(1，2)—M 模型，估计结果如下(括号内为z统计量值):

然后，对估计的 ARMA(1，2)—GARCH(1，2)—M 模型进行残差诊断，检验结果显示，滞后1期F统计值为0.8691，对应 P值为0.3553，滞后15期 F统计值为0.3566，对应 P 值为0.9575。因此，可以认为，ARMA(1，2)—GARCH(1，2)—M模型的残差已不具有ARCH或GARCH 效应了，与 ARMA(1，2)—GARCH(1，1)—M 模型相比，我们认为前者更为理想。根据上述ARMA(1，2)—GARCH(1，2)—M模型估计的结果，均值方程(10)中GARCH项的系数(为-1.596)在5% 的置信水平下不显著，但在10% 的置信水平下显著。同时，方差方程(11)中的GARCH(-1)项的系数在10% 的置信水平下不显著，而GARCH(-2)项的系数在1% 的置信水平下显著。由于均值方程(10)中GARCH项的系数为负值，因此，我们可以认为，我国经济波动与经济增长之间存在负相关关系。换句话说，我国经济波动幅度越大，越不利于经济的增长，经济波动幅度越小，经济增长率越高，这与Keynes和Woodford的理论研究以及陈太明利用GARCH—M模型得出的结果相一致。

四、结论与政策建议

从我国1953—2011年的人均国内生产总值增长率数据来看，新中国成立后到改革开放前的一段时间内，宏观经济运行波动幅度比较大，经济进步缓慢，并逐步落后于西方国家。众所周知，新中国成立后，经过“一化三改”运动，我国逐渐建立了社会主义制度，实行高度集中的政治体制和计划经济体制。为实现超英赶美，我国大部分资源投资于重工业领域，短期内，各种生产指标超额完成，经济出现了快速增长。但是，这种畸形化的发展导致了资源配置极度失衡，更埋下了巨大的经济波动风险，一段时间内，国民经济陷入倒退，特别是1961年，人均国内生产总值增长率达到最低值，为-26.6%。正是这种不遵守经济发展规律的命令式计划经济体制，导致了经济的大起大落。改革开放后，随着我国经济市场化改革不断推进，特别是在我国加入WTO之后，我国经济与世界的联系更加紧密，我国经济的抗风险能力和经济稳定性显著增强。在政府的宏观调控下，经济波动得到了控制，经济飞速发展，创造了经济奇迹，这恰恰从经验事实方面论证了我国经济波动对经济增长具有负向影响。

凯恩斯学派认为，市场经济本身具有不稳定性，宏观经济运行经常低于充分就业水平，为应对有效需求不足的问题，政府应该加强对宏观经济的干预。与凯恩斯学派不同，新古典学派则认为市场经济具有“自动稳定器”功能，当出现经济波动时，经济会自发地恢复到充分就业状态，而经济的大起大落恰恰是政府本身的行为所致。因此，新古典学派不赞成政府对经济的干预。

综合以上分析，可以得到一些启示:

第一，政府很有可能成为经济波动的原因之一，要充分考虑到政府自身行为对经济波动的影响。我国的历史数据已经表明，在改革开放前的计划经济体制下，政府的行为造成经济运行的大起大落，成为经济的波动源，从而抑制了经济的增长。改革开放后，市场化改革使得政府减少了对经济的直接干预，经济稳定性变强，抗风险能力得到了提升，经济持续增长。如果政府对经济干预过多，难免产生错误的决策，这样造成更大的经济波动而影响我国经济的增长。因此，政府应该提高认识，必须继续推进市场经济体制改革，减少政府对经济不必要的干预，把市场能做的交给市场，不断完善社会主义市场经济体制。

第二，要不断提高政府宏观调控水平。政府应该减少对经济不必要的干预，做到不越位，但这并不代表政府无所作为。当发生经济危机或者经济不景气时，经济的波动会给整个社会福利带来巨大的损失。这个时候，需要政府的果断出击，帮助市场建立信心，以免使经济波动过大，而影响到经济的增长。就如凯恩斯学派所认为的，当经济处于萧条状态，有效需求不足，政府应该实施扩张的财政政策和货币政策，以增加有效需求，提高社会产出水平，保持经济的增长;而当经济超过充分就业水平时，通货膨胀水平上升，这时，政府也应该逆经济风向行事，把握好时机，实施紧缩的财政政策和货币政策，适当地减少有效需求，使经济更加平稳地运行。

第三，在我国进行市场化改革的过程中，应注意把控好改革的节奏，在时机不成熟的情况下改革步伐不要迈得过快。20世纪90年代初的俄罗斯和东欧国家实施的所谓“休克疗法”，在短时间内引起了巨大的经济波动，给东欧和俄罗斯人民的生活带来了巨大冲击，甚至引发了社会的动荡。这种激进的市场化改革并没有带来经济的增长，反而抑制了经济的发展。因此，我国应该汲取俄罗斯和东欧国家的经验教训，实行渐进式的市场化改革，以减少经济的波动，并促进经济的增长，维护社会的稳定。

第四，我国政府还应该利用自身的政治优势，合理应对经济波动。比如，欧美一些国家，执政党往往事先承诺保持低通胀，但是由于大选的需要，改而采取扩张性的宏观经济政策，以提高就业水平。这样就出现了“动态不一致性”的问题，不利于维护政府的公信力。此外，由于反对党的存在，当经济产生巨大波动时，欧美一些国家应对政策的实施需要经过议会漫长的讨价还价，这样很有可能错失良机，对经济造成进一步的伤害。相比之下，我国政府在面对经济波动时，在很大程度上能够摆脱这一困扰，迅速实施相应的经济政策，减少社会福利的损失。

[1]Jacobs.J.Econometric Business Cycle Research.The Netherlands：Kluwer Academic Publishers，1998.

[2]Keynes，J.M.The General Theory of Employment，Interest，and Money.London：Macmillan， 1936.

[3]Bernanke，B.S.Irreversibility，uncertainty ad cyclical Investments.Quarterly Journal of Economics， 1983，Vol.23.

[4]Woodford，M.Learning to Believe In Sunspots.E-conometrica，1990，Vol.58.

[5]Turnovsky，S.J.， and Chattopadhyay， P.Volatility and Growth in Developing Economies：Some Numerical Results and Empirical Evidence.Journal of International Economics， 2003，Vol.59.

[6]Zarnowitz，V.and Geoffrey， M.Major Changes in Cyclical Behaviour. Chicago：University of Chicago Press，1986.

[7]Ramey， G.and Ramey， V.Cross-country Evidence on the Link between Volatility and Growth.American Economic Review，1995，Vol.85.

[8]Martin，P.and Rogers，C.A.Long-term and Short-term Economic Instability.European Economic Review，2000，Vol.44.

[9]Kneller，R.A.and Young， G.Business Cycle Volatility，Uncertainty and Long-run Growth.Manchester School，2001，(69).

[10]Fatas，A.The Effects of Business Cycles on Growth.N.Loayza and R.Soto(eds.).Economic Growth:Sources， Trends and Cycles.Santiago：Central Bank of Chile，2002.

[11]Kormendi，R.and Meguire，P.Macroeconomic Determinants of Growth：Cross-Country Evidence.Journal of Monetary Economics，1985，Vol.16.

[12]Grier，K.and Tullock， G.An Empirical Analysis of Cross-national Economic Growth，1951-80.Journal of Monetary Economics，1989，Vol.24.

[13]Caporale， T.and McKiernan，B.The Relationship between Output Variability and Growth：Evidence from Post-war UK Data.Scottish Journal of Political Economy，1996，Vol.43.

[14]李永友.经济波动对经济增长的减损效应：中国的经验证据[J].当代经济科学，2006，(4).

[15]杜两省，齐鹰飞，陈太明.经济波动对中国经济增长影响的稳健性研究[J].云南财经大学学报，2011，(4).

[16]周达军.我国经济波动对增长的负面效应的实证分析[J].经济管理，2007，(14).

[17]杨秋宝.经济发展总体转型的选择：从高速经济增长转向适度经济增长[J].企业经济，2011，(12).

[18]闫素仙，张建强.中国外汇储备汇率结构风险研究——基于VaR-GARCH模型的实证研究[J].河北经贸大学学报，2012，(1).

[19]卢二坡，王泽填.短期波动对长期增长的效应——基于省际面板数据的经验证据[J].统计研究，2007，(6).

[20]陈昆亭，周炎，龚六堂.短期经济波动如何影响长期增长趋势?[J].经济研究，2012，(1).