运用焦半径公式 速解焦点弦问题

●

(北仑中学 浙江宁波 315800)

运用焦半径公式速解焦点弦问题

●马洪炎

(北仑中学 浙江宁波 315800)

文献[1]介绍了一道解析几何试题(椭圆中涉及焦点弦的问题)的2种解法及教学过程，笔者阅后受益匪浅.经研究还发现对于圆锥曲线过焦点弦的问题还有更加简捷的解法，现介绍如下，供大家参考．

通常把圆锥曲线上的点P与圆锥曲线的焦点F的连线段PF称为圆锥曲线过点P的焦半径．文献[1]中介绍的解法2之所以比解法1要简捷许多，其主要原因是在解法2中注意到椭圆的焦半径公式|AF|=a-ex0(不妨称为坐标形式)的应用.本文先介绍一组圆锥曲线的焦半径公式的另一种形式(不妨称为角度形式)，然后简单介绍其应用．

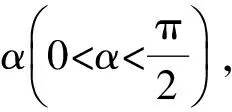
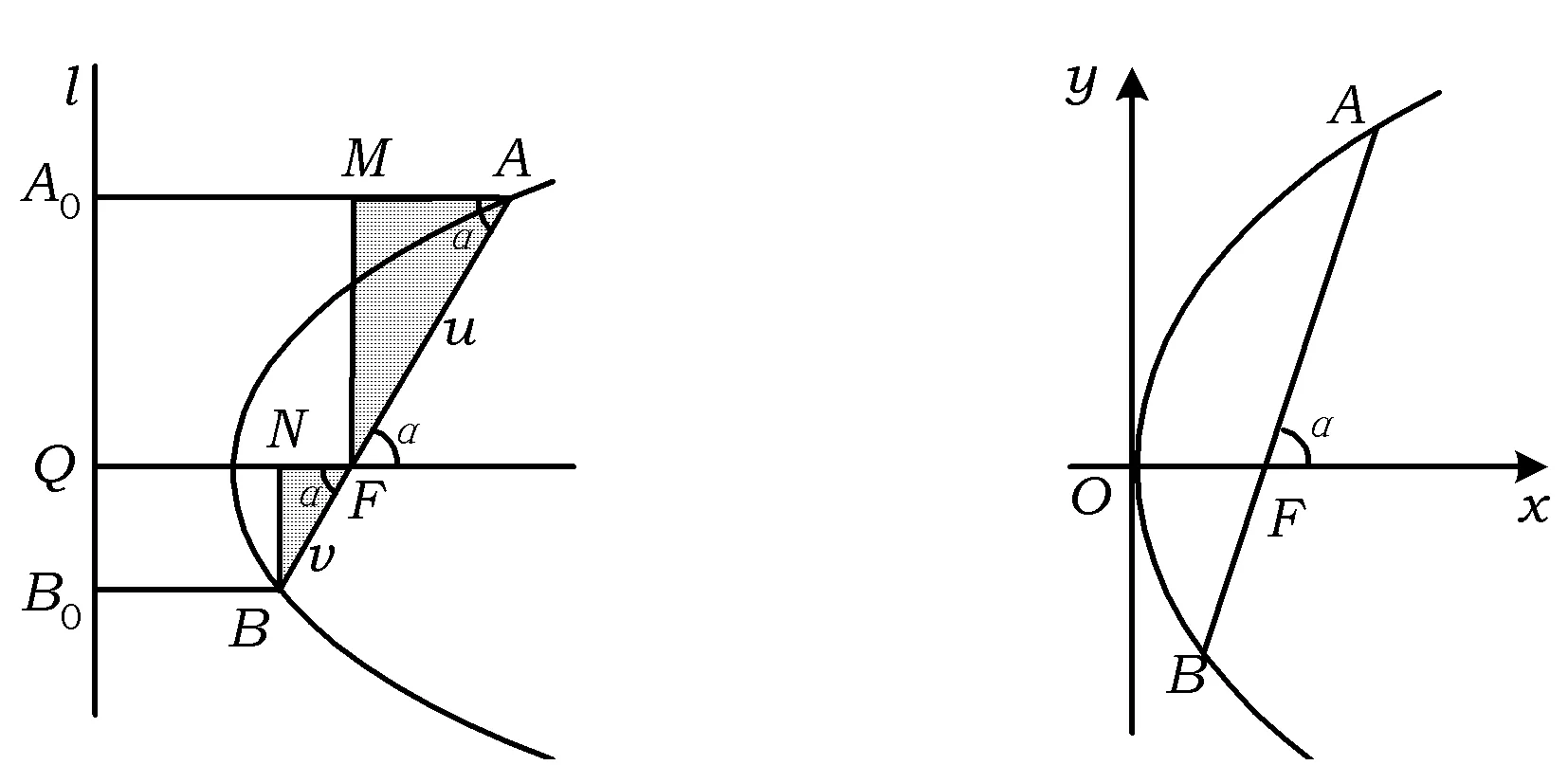
图1 图2

证明如图1,作FQ⊥l于点Q，则|FQ|=p，作AA0⊥l于点A0，BB0⊥l于点B0，FM⊥AA0于点M，BN⊥FQ于点N.令|FQ|=u,|BF|=v，则

在Rt△AFM中，

|AM|=|AF|cosα=ucosα,

即

解得

在Rt△BFN中，

|FN|=|BF|cosα=vcosα，

即

解得

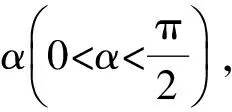
(对于抛物线x2=2py也有类似性质.)

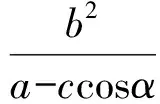
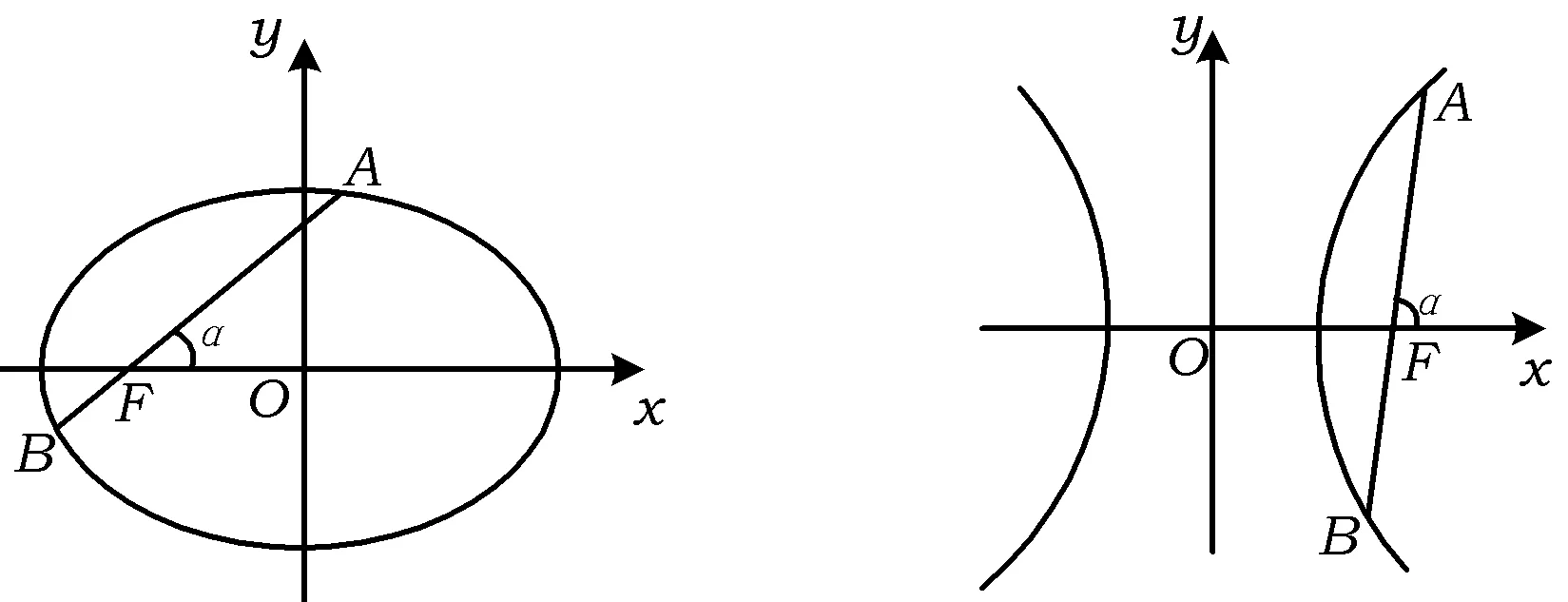
图3 图4

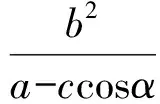
2 公式的简单应用

2.1 计算焦半径及过焦点的弦长

图5

(1)若直线l斜率为1，求直线l′的方程;

分析本题第(2)小题是一个典型的解析几何定值问题,通常可运用函数的思想方法解之,其解题过程可归纳为：一选，二求，三定值.具体操作程序如下:

一选:选择参变量.需要证明为定值的量在通常情况下应该是变量,它应该随某一个量的变化而变化,可选择这个量为参变量．

二求:求出函数的解析式.即把需要证明为定值的量表示成关于上述参变量的函数．

三定值:化简函数解析式得到定值.由题目的结论可知要证明为定值的量必与参变量的大小无关,故求出的函数必为常数函数,因此,只需对上述函数的解析式进行必要的化简即可得到定值．

文献[1]介绍的解法1(复杂解法)选择以直线AB的斜率k为目标函数的变量;解法2(简捷解法)选择线段AB的中点N的横坐标为目标函数的变量.在运用函数的思想方法解决定值问题时,目标函数变量的选择显得很重要.由于角度形式的焦半径公式与本题相关的线段可直接对话,因此也可选择直线AB与x轴的夹角α为目标函数的变量.

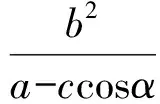
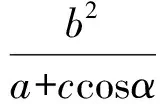
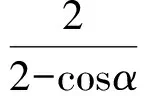
设AB的中点为N,则

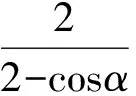
即

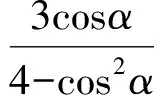
在Rt△MNF中，

评注直线AB与x轴夹角为α的几何意义更加明确,运算过程显得更简捷.运用这种解法,不难得到第(2)小题更一般的结论．

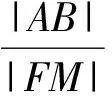
图6

(浙江省名校新高考研究联盟2013届第一次联考试题改编)

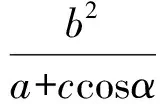
从而

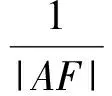
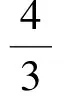
2．2 求2条焦半径的比值

(2008年江西省数学高考理科试题)

解由题意可知,直线AB与抛物线对称轴(y轴)的夹角α=60°,且|BF|>|AF|,由推论1可知

于是

2.3 求焦点弦所在直线的斜率或倾斜角

( )

(2010年全国数学高考理科试题)

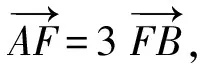
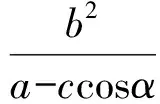
从而

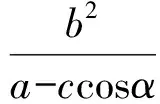
即

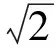
2.4 求圆锥曲线的离心率或标准方程

( )

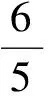
(2009年全国数学高考理科试题)

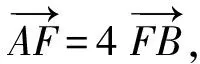
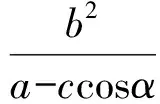
从而

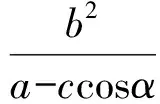
即

4(a-ccos60°)=a+ccos60°,

(1)求椭圆C的焦距；

(2010年辽宁省数学高考文科试题)

解(1)椭圆C的焦距2c=4(过程略)．

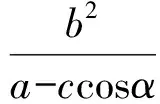
从而

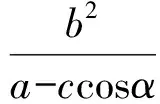
即

2(a-ccos60°)=a+ccos60°,

圆锥曲线中涉及“焦点弦”、“焦半径”问题一直是高考和竞赛中的热点问题之一.选择相关直线的斜率为参变量解决问题时，一般的操作过程是把直线方程代入曲线方程，得到关于x的一元二次方程，然后利用韦达定理解决之，运算量往往较大.若运用角度形式的焦半径公式，则可简化运算过程，直达问题结论，收到事半功倍的效果．

[1] 崔志荣,薛宗华.一道解析几何题运算教学的实践与思考[J].中学教研(数学),2013(1)：13-15.