形式化与非形式化在课堂教学中的融合演绎

●

(乐清中学 浙江乐清 325600)

形式化与非形式化在课堂教学中的融合演绎

●徐建荣

(乐清中学 浙江乐清 325600)

高中数学新课程从总体上来说，是为学生学习必需的、有用的数学，删减了不必要的、陈旧的数学内容，一定程度上减少了学生的学习压力，从出发点来说值得肯定．其减少了形式化数学的结果、证明等，大大加深了感性认知等非形式化手段在数学教学中的运用，但如何把握这两者的完美融合仍然是教学的一个难题．

近几年浙江省关于高中数学新课程进行了很多相关的学习、交流，笔者也参与观摩了很多的公开课.如今的公开课与时俱进，更多关注学生的“参与度”、课堂的“新鲜感”等教学理念渗透.辩证来看:既不能过于强调“参与度、情境和探究”，也不能一味保守,总是采用传统的“启发式教学”．现实中，如今的常态课还走在过于形式化、启发式教学的误区，而公开课却行走在完全非形式化、情境式教学的误区．结合当今的高中数学教学，笔者认为：高中数学中“形式化的结果”仍比较常见(诸如函数的概念、平面向量基本定理等)，而“非形式化的数学”往往能让学生对数学知识的表象理解和记忆，但却无法指导学生到达数学概念的彼岸——窥视其规律与本质(如数形结合以形辅数、函数与方程思想等)．在新课程理念下，就如何结合形式化与非形式化的数学教学，笔者有一些不成熟的想法与大家分享．

1 概念对比

形式化和非形式化一直是数学教学中的两大产物，其特点主要围绕下面5点进行界定和区分：

表1 形式化与非形式化的数学教学

2 融合教学

《普通高中数学课程标准》明确指出：在数学教学中，学习形式化的表达是一项基本要求，但是不能只限于形式化的表达，要强调对数学本质的认识，数学的现代发展也表明，全盘形式化是不可能的，因此，高中数学课程应该返璞归真，把数学的学术形态转化为学生易于接受的教育形态[1]．

“数学形式化”犹如旧版教材一直提倡的“启发式教学”，而“非形式化”恰恰犹如新课程所一直提倡的“情境式教学”，我们不能说“数学形式化”完全不符合高中学生的认知，好比完全否定“启发式教学”毫无优点一样，也没有任何证据说明“非形式化”就能让高中生更透彻地理解数学概念、定理等，好比“情境式教学”就远比“启发式教学”优秀，有种高高在上的感觉一样[2]．

张奠宙教授说过：数学教育要注重认知，淡化形式，但是不能丢了形式化——淡化(对中学生而言)并非完全否定，只是小学生、中学生、大学生各种年龄阶段的学生都要按照不同形式化程度来教学．笔者认为，对高中生数学课堂教学应该介于形式化和非形式化之间，即适度的形式化更符合高中生的认知心理．

3 特点分析

形式化是数学特有的产物，从旧的人教版教材开始，形式化一直是中学数学的特点，似乎没有形式化，数学就不是数学．刘绍学教授语：以往的中学课堂，教师首先给学生介绍一个数学的定理，然后进行严密的证明，进而对定理进行几点注意，最后使用定理解决数学问题．这种数学课是形式化比较明显的，在以往看来，这样的数学教学有几个好处：

(1)数学知识的传授连贯，教师教学比较方便；

(2)数学定理的证明比较严密，使得学生心服口服；

(3)数学知识基本一步到位，在某个定理处进行变式教学、反复演练，熟悉为止．

但是形式化的数学渐渐显现出不足，主要有：

(1)对高中生而言，是不是也要学那么形式化的数学呢？反之，如果淡化一点，会不会有更好的教学效果？

(2)是不是每个人将来都会用到这么形式化的数学呢？

(3)数学都要追求形式化，是不是太费神费力？

随着新课程改革的不断深入，作为教材主导地位的形式化数学渐渐走下神坛，取而代之的是新教材，新教材较明显地弱化了形式化的数学在高中数学中的地位．因此，“如何融合两者，如何在教学中进行完美的渗透”是教师教学的一种境界.下面以笔者观摩的一堂公开课“数学归纳法(第一课时)”为例进行分析说明.

4 教学案例

4.1 非形式化阶段——创设情境，思考问题

探究1人工探索

探究2智能探索

结合程序语言，给出如图1所示的框图：

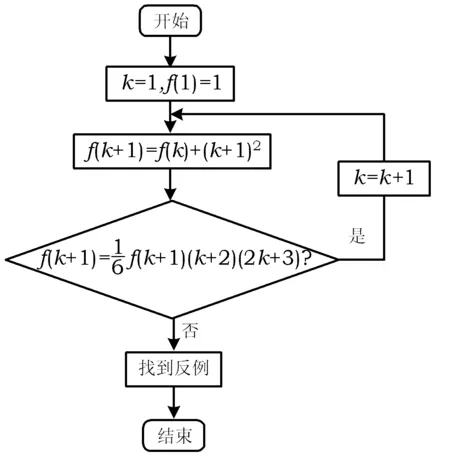
图1

探究3可行性探讨

由学生来探讨这个智能探索是否可行，能否达到证明的目的．

设计意图由学生熟悉的3个连续探究引入本节课，符合学生的认知规律看似没有给出数学归纳法，实质上已经让学生从潜意识中接触到了数学归纳法的适用范围，这种探究式的教学可以让学生亲临数学归纳法的形成过程，逐渐感受数学归纳法的必要性与必须性，加深对概念的理解，并且在一次次的探究收获中慢慢接触数学归纳法的关键，尤其在首次接触中显得尤为重要．

4.2 形式化初步阶段——层层递进，诱发思维

在上述探究的基础上，学生明白以上办法都不能证明，因此接下来在“非形式化阶段”的基础上继续思考和提炼.这个提炼的过程也许对于学生来说会比较抽象，但必不可少，这个过程需要教师的正确点拨和引导.经历了这个过程，学生就会对数学归纳法的基础和依据有深刻的理解．

直面无限，我们真的束手无策？接下来通过类比等差、等比数列完成探究4.

探究4类比探索

表2 类比等差、等比数列

由表2得到探究收获：类比数列中处理无限的方法，可以得到一种全新、巧妙的证明方法．

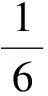
设计意图通过上述几个问题及探究，已经明确给出了数学归纳法的过程，教师以等差、等比数列对应为学生的“最近发展区”，抽象得出证明一个命题成立的过程.这正是一种类比推理的思想和建构的过程．通过对一个具体问题的深入研究，得到了一种新的数学概念，也得到了数学归纳法的本质．

4.3 形式化与非形式化融合——明确概念，活学活用

在上述基础上，进一步思考：

问题3新的证明方法适合于哪种题型？

问题4你能总结出新证明方法的解题步骤吗？

由此给出本节课的课题：数学归纳法，同时很自然地给出了数学归纳法的解题步骤．

问题5你能用数学归纳法来解析多米诺骨牌游戏吗？

设计意图在“非形式化阶段”到“形式化阶段”的基础上，通过抽象的概况，给出了数学归纳法的适用范围和明确的解题步骤，并且及时对关键性步骤、易错知识点进行点拨，使学生成功地完成了质的飞跃．

4.4 形式化最终阶段——错误辨析，思维升华

(1)与数学归纳法有关的美丽误会：费马质数(当p是质数时，22p+1是质数)直到费马去世后67年，著名的数学家欧拉才证明了这个命题的错误性．

(2)有人声称证明了“所有的奇数都是2的倍数”．

最后进行课堂小结，用3个英语单词总结——数学归纳法学习的“why？where？what？”来结束本堂公开课．

设计意图在学生已经掌握数学归纳法本质及步骤的情况下，给出反例辨析：第1个反例缺递推；第2个反例缺基础，由此进一步让学生理解2个步骤缺一不可．最后的3个单词进一步帮助学生进行反思：为什么要用数学归纳法，什么时候用数学归纳法，怎么用数学归纳法．整堂课如行云流水一般把形式化和非形式化自然融合，通过对一个具体题目的层层递进研究，得到了本节课对概念学习的从形象到抽象的过程，是形式化数学用非形式化手段完美演绎的一节公开课．

5 教学思考

高中数学课堂教学比较合适的方式，是有机融合形式化和非形式化的运用，将启发式教学与情境式教学恰当地整合，其主要目的是通过整合创新教学模式，使得以学生为主体的教学理念设计不是一句空话，其优点在于充分发挥学生的参与性，无论是后进生还是优等生，在其各自不同的范围之内(大多数学生更容易接受感性非形式化的数学，少数则比较容易把握形式化的数学结果)对数学知识和问题的不同层次进行不同程度的涉及，真正落实新课程重要的开发理念：注重对数学知识形成过程的学习，淡化过于形式化的结果与证明．

笔者最后想说，高中数学课堂教学有很多方面值得我们关注，笔者从“数学归纳法”案例入手，分享了如何进行有机融合非形式化和形式化的教学策略.在教学时，教师要注意对高中学生采用的教学方法，既不能一味“情境化”(过于直觉、感官)，也不能“形式化、启发式教学”过度.只有2条腿走路，才能使学生能体验和感悟到数学思维的理性精神，才能做到与时俱进的有效教学．

[1] 罗展华.高中数学教学中形式化与非形式化表现特征[J].中学教研(数学),2009(4):12-14.

[2] 张焕明.浅论素质教育观下的数学课题设计[J].中学教研(数学),2002(4)：8-11.

[3] 张继红.创新教育下中学数学课堂教学模式研究[D].长春：东北师范大学，2002.

[4] 涂荣豹.论数学活动的过程知识[J].数学教育学报,2002(11)：9-13.